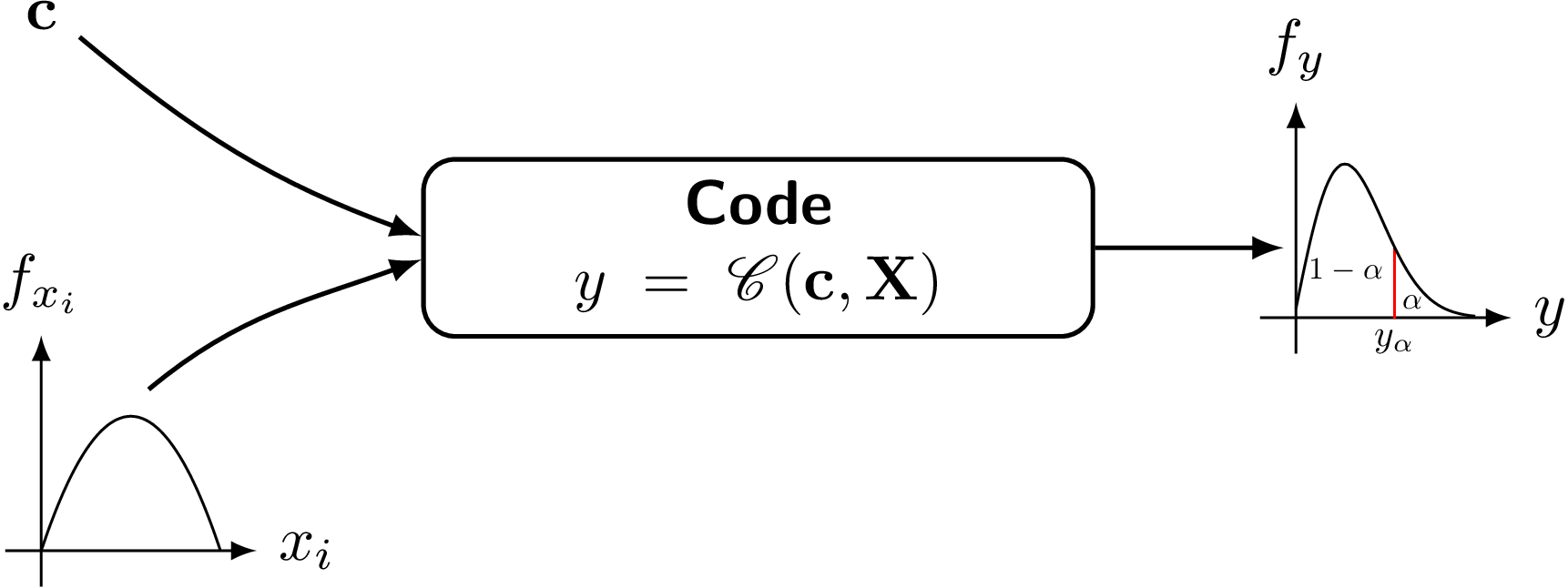Documentation / Methodological guide :

Chapter III. The Sampler module

Chapter III. The Sampler module

Chapter III. The Sampler module

Abstract

This part is a description of the method used to produce the design-of-experiments, which is a crucial part in uncertainty propagation but also for sensitivity analysis and surrogate model generation.

Table of Contents

III.1. Introduction

III.2. The Stochastic methods

III.2.1. Introduction
III.2.2. Correlating samples drawn from different marginals
III.2.3. The maximin LHS
III.2.4. The constrained LHS

III.3. QMC method

III.1. Introduction

The Uranie-sampling module is used to produce design-of-experiments knowing the expected behaviour of the input variables for the problem under consideration. The framework of our approach can be illustrated in the following schematic view:

Figure III.1. Schematic view of the input/output relation through a code

We will denote as 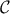the studied computational code which, generally, has two types of inputs:
- The constant parameters which are gathered in the vector 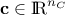. They represent constants.
- The uncertain parameters which are gathered in the vector
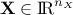
  It shall be noticed that these parameters are supposed to be uncertain either because of a lack of knowledge on their actual value or because of their intrinsic random nature.
The result of the code 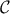for a given set of parameters 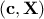gives the vector 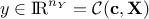which contains all the output variables of the analysis.

Most of the time, the code 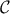implies solving equations with partial derivatives in more or less complex configurations. The most well-known method to handle this is to generate a sample, as representative as possible of the behaviour of all input variables, in order to fully cover the input parameter phase space. This is the definition of a design-of-experiments which can be generated in many different ways (depending on the analysis purpose, the laws under consideration...). The rest of this section mainly introduces concepts used throughout this documentation; more details can be found either in the user manual or in references.

Different methods exist to obtain a design-of-experiments from uncertain parameters which can be classified into two categories:

stochastic methods (see Section III.2). These methods consist in using a random number generator to produce new samples. This is also called Monte-Carlo.
deterministic methods (see Section III.3). Two distinct calls with the same parameters will always give the same point in a design-of-experiments. Some of these methods (those discussed below) are sequences which are sometimes called quasi-Monte Carlo (qMC).


II.3. Combining these aspects: performing PCA		III.2. The Stochastic methods