Introduction générale
Avec l'avènement de l'informatique récent, le rôle de la simulation numérique devient prédominant car cette dernière peut profiter de l'augmentation des ressources de calcul mais surtout de leur parallélisation. Elle est alors de plus en plus utilisée dans le processus de l'aide à la prise de décision, ce qui sous entend qu'elle n'est plus forcément seulement descriptive mais qu'elle se doit de devenir de plus en plus prédictive et ce, en étayant de la manière la plus fine possible la confiance que l'on peut avoir dans ses prédictions.
Dans cette partie, nous discuterons un système 𝓢, dont le design (les dimensions, les matériaux, les conditions initiales, ...) est caractérisé par un vecteur x ∈ X, et qu'on peut tenter de modéliser de différentes manières. Les différents niveaux de modélisation introduisent ainsi des sources possibles d'incertitudes et de biais qui sont discutées par la suite.
1. un modèle mathématique pour décrire parfaitement certaines variables d'intérêt du système (qu'on appellera par exemple y(x) ∈ Y
Ce modèle n'est pas forcément connue ou même atteignable mais décrit la "la réalité";
2. un modèle paramétrique ysim(•) décrivant le mieux possible les mêmes variables d'intérêt du système (ce modèle étant non forcément égal au précédent niveau). Ce dernier est normalement représentatif de la compréhension du système et nécessite deux types de paramètres :
- les paramètres d'entrée, simulés ou mesurés, xξ ∈ Xin qui sont les facteurs dont le modèle paramétrique dépend pour chaque estimation (le vecteur ξ pouvant être remplacé par xmes ou xsim suivant que les paramètres d'entrée aient été mesurés ou simulés);
- les paramètres de la simulation θ (aussi appelés paramètres du modèle) qui sont, souvent, des paramètres constants;
3. un algorithme capable de calculer correctement le modèle paramétrique, si possible sans erreur, mais nécessitant parfois aussi des paramètres dédiés :
- les paramètres permettant la convergence numérique des algorithmes νnom;
4. des mesures des variables d'intérêt du système (ymes);
Ces différents niveaux peuvent être schématiquement représentés dans la 1)a) où la " réalité "(en noir) est plus ou moins bien décrite par les 3 autres niveaux d'abstraction : le modèle paramétrique idéale (en rouge), son implémentation sous forme d'algorithme (en bleu) et les mesures expérimentales faites (en vert).
FIGURE 1 - (a) Zone de représentation (schématique) des différents niveaux d'abstraction des variables d'intérêt du système. (b) Relation entre les différents niveaux d'abstraction.
De cette vision découle l'approche VVUQ (pour Verification, Validation and Uncertainty Quantification) dans laquelle il faut définir un certain nombre de concepts :
Validation : cette étape tente de maîtriser les incertitudes de simulation εsim := ytrue - ysim (•, θ, νnom) qui pourraient naître d'une trop grande simplification du phénomène. Un modèle validé n'est toutefois pas un modèle parfait car cette validation peut être faite sur des grandeurs spécifiques et / ou dans un domaine d'utilisation bien défini (souvent restreint, mais suffisant). Elle est souvent résumée comme "Résoudre l'équation correcte".
Vérification : cette étape tente de maîtriser les incertitudes d'implémentation du modèle numérique εnum := ymod (•, θ) - ysim (•, θ, νnom) qui pourraient naître d'un problème de convergence de maillage, d'un problème d'arrondi dans l'arithmétique flottante, de bugs... Elle est souvent résumé comme " Résoudre correctement l'équation".
Calibration : cette étape, nécessaire une fois que la validation et la vérification sont faites, tente de définir la valeur optimale des paramètres du modèle θ et de maîtriser les incertitudes liées εθ. Dans la figure 1b, elle est intégrée au processus de " Model validation (operationnal) ", cette dernière comprenant, en sus, les incertitudes liées au choix de la modélisation des incertitudes des paramètres d'entrée.
Propagation d'incertitude : cette étape tente d'estimer l'impact des incertitudes des paramètres d'entrée sur les variables d'intérêt et plus généralement sur les grandeurs d'intérêts (une grandeur d'intérêt est une donnée numérique, généralement statistique, représentative de la distribution de la variable d'intérêt : la moyenne, l'écart-type,un quantile,...).
Bien souvent, dans l'approche probabiliste, il est fréquent de considérer que la validation(conceptuelle) du modèle et sa vérification sont faite avant de considérer faire une analyse de quantification d'incertitude plus poussée.
Les principales étapes discutées ci-dessus et dans le reste de ce chapitre sont regroupées dans la Figure 2 qui montre la définition du problème, c'est à dire du processus, la quantification des sources d'incertitudes, la propagation des incertitudes et l'analyse de sensibilité.
Aléatoire : aussi appelé statistique dans certains domaines, ces incertitudes représentent la variabilité naturelle de certains phénomènes.
Epistémique : ces incertitudes sont généralement plus complexes car elles traduisent un manque de connaissance portant sur les valeurs particulières de certains paramètres, ou sur des lois physiques sous-jacentes.
Une autre caractéristique parfois discutée pour dissocier les incertitudes est leur côté réductible ou irréductible. Celles appartenant à la première catégorie peuvent être contrainte avec un nouvel apport de données, tandis que celles issues de la seconde ne peuvent être plus contenues. Il est coutumier de dire que les incertitudes épistémiques sont réductibles tandis que les incertitudes aléatoires sont irréductibles.
Toutefois cette distinction n'est pas si claire car elle peut dépendre du point de vue et des buts : l'incertitude sur la durée de vie d'un composant, si elle vous est fournie, est à considérer comme une incertitude aléatoire, mais si vous êtes le constructeur du dit composant, vous pouvez choisir de l'utiliser ainsi ou de lancer un processus de R&D pour améliorer le processus de fabrication et tenter de réduire cette dernière. Le coût acceptable (économique, temporel, structurel...) de la réduction rentre souvent en compte.
Dans cette partie, nous discuterons un système 𝓢, dont le design (les dimensions, les matériaux, les conditions initiales, ...) est caractérisé par un vecteur x ∈ X, et qu'on peut tenter de modéliser de différentes manières. Les différents niveaux de modélisation introduisent ainsi des sources possibles d'incertitudes et de biais qui sont discutées par la suite.
I. Vision générale de la simulation numérique
La capacité prédictive de la simulation numérique implique qu 'on définisse plusieurs niveaux d'abstraction, non mutuellement exclusif, dont le but est la description du réel la plus fidèle possible :1. un modèle mathématique pour décrire parfaitement certaines variables d'intérêt du système (qu'on appellera par exemple y(x) ∈ Y
Ce modèle n'est pas forcément connue ou même atteignable mais décrit la "la réalité";
2. un modèle paramétrique ysim(•) décrivant le mieux possible les mêmes variables d'intérêt du système (ce modèle étant non forcément égal au précédent niveau). Ce dernier est normalement représentatif de la compréhension du système et nécessite deux types de paramètres :
- les paramètres d'entrée, simulés ou mesurés, xξ ∈ Xin qui sont les facteurs dont le modèle paramétrique dépend pour chaque estimation (le vecteur ξ pouvant être remplacé par xmes ou xsim suivant que les paramètres d'entrée aient été mesurés ou simulés);
- les paramètres de la simulation θ (aussi appelés paramètres du modèle) qui sont, souvent, des paramètres constants;
3. un algorithme capable de calculer correctement le modèle paramétrique, si possible sans erreur, mais nécessitant parfois aussi des paramètres dédiés :
- les paramètres permettant la convergence numérique des algorithmes νnom;
4. des mesures des variables d'intérêt du système (ymes);
Ces différents niveaux peuvent être schématiquement représentés dans la 1)a) où la " réalité "(en noir) est plus ou moins bien décrite par les 3 autres niveaux d'abstraction : le modèle paramétrique idéale (en rouge), son implémentation sous forme d'algorithme (en bleu) et les mesures expérimentales faites (en vert).
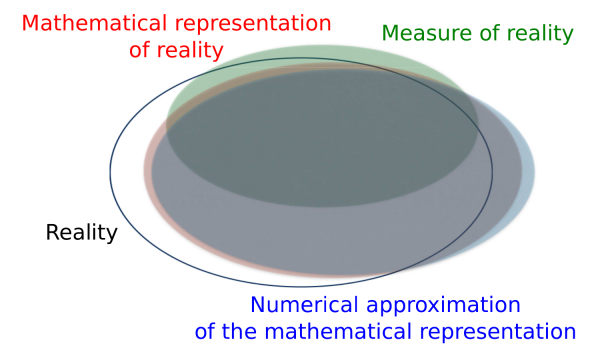
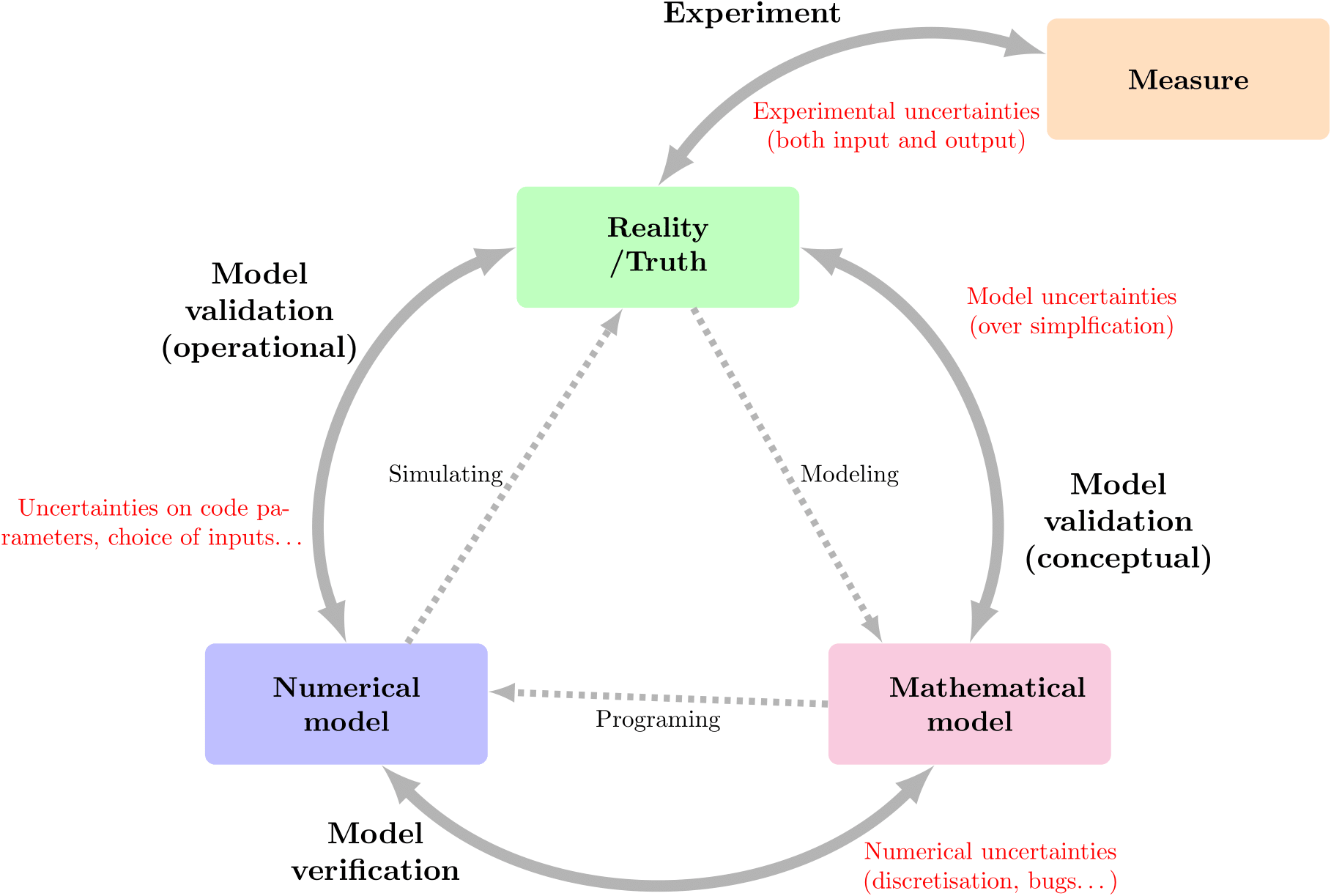
FIGURE 1 - (a) Zone de représentation (schématique) des différents niveaux d'abstraction des variables d'intérêt du système. (b) Relation entre les différents niveaux d'abstraction.
De cette vision découle l'approche VVUQ (pour Verification, Validation and Uncertainty Quantification) dans laquelle il faut définir un certain nombre de concepts :
Validation : cette étape tente de maîtriser les incertitudes de simulation εsim := ytrue - ysim (•, θ, νnom) qui pourraient naître d'une trop grande simplification du phénomène. Un modèle validé n'est toutefois pas un modèle parfait car cette validation peut être faite sur des grandeurs spécifiques et / ou dans un domaine d'utilisation bien défini (souvent restreint, mais suffisant). Elle est souvent résumée comme "Résoudre l'équation correcte".
Vérification : cette étape tente de maîtriser les incertitudes d'implémentation du modèle numérique εnum := ymod (•, θ) - ysim (•, θ, νnom) qui pourraient naître d'un problème de convergence de maillage, d'un problème d'arrondi dans l'arithmétique flottante, de bugs... Elle est souvent résumé comme " Résoudre correctement l'équation".
Calibration : cette étape, nécessaire une fois que la validation et la vérification sont faites, tente de définir la valeur optimale des paramètres du modèle θ et de maîtriser les incertitudes liées εθ. Dans la figure 1b, elle est intégrée au processus de " Model validation (operationnal) ", cette dernière comprenant, en sus, les incertitudes liées au choix de la modélisation des incertitudes des paramètres d'entrée.
Propagation d'incertitude : cette étape tente d'estimer l'impact des incertitudes des paramètres d'entrée sur les variables d'intérêt et plus généralement sur les grandeurs d'intérêts (une grandeur d'intérêt est une donnée numérique, généralement statistique, représentative de la distribution de la variable d'intérêt : la moyenne, l'écart-type,un quantile,...).
Bien souvent, dans l'approche probabiliste, il est fréquent de considérer que la validation(conceptuelle) du modèle et sa vérification sont faite avant de considérer faire une analyse de quantification d'incertitude plus poussée.
Les principales étapes discutées ci-dessus et dans le reste de ce chapitre sont regroupées dans la Figure 2 qui montre la définition du problème, c'est à dire du processus, la quantification des sources d'incertitudes, la propagation des incertitudes et l'analyse de sensibilité.
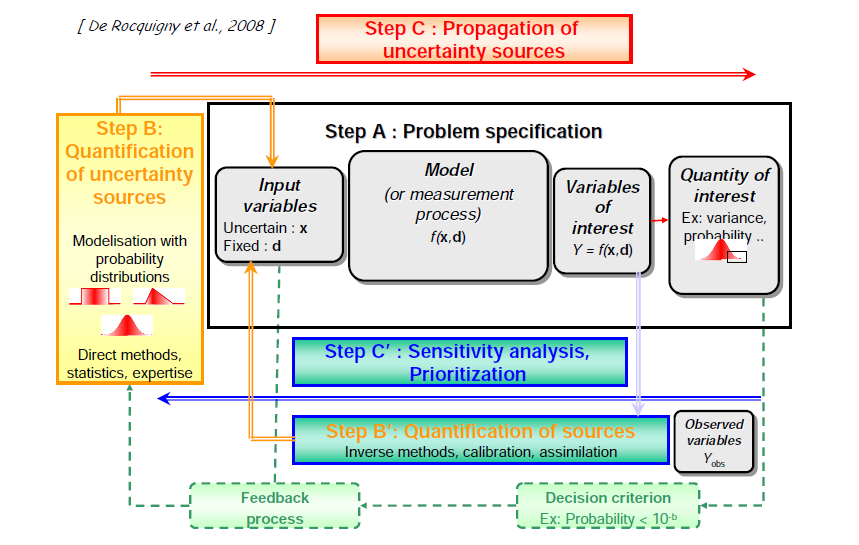
FIGURE 2 – Représentation schématique de plusieurs étapes de l’approche VVUQ
II. Nature des incertitudes et modélisation
En considérant ici la propagation des incertitudes (suivant l'hypothèse que le modèle est conceptuellement validé et vérifié), il est intéressant de se poser des questions sur les propriétés des incertitudes que l'on souhaite prendre en compte. La littérature discute souvent ces dernières en divisant leur nature en deux catégories:Aléatoire : aussi appelé statistique dans certains domaines, ces incertitudes représentent la variabilité naturelle de certains phénomènes.
Epistémique : ces incertitudes sont généralement plus complexes car elles traduisent un manque de connaissance portant sur les valeurs particulières de certains paramètres, ou sur des lois physiques sous-jacentes.
Une autre caractéristique parfois discutée pour dissocier les incertitudes est leur côté réductible ou irréductible. Celles appartenant à la première catégorie peuvent être contrainte avec un nouvel apport de données, tandis que celles issues de la seconde ne peuvent être plus contenues. Il est coutumier de dire que les incertitudes épistémiques sont réductibles tandis que les incertitudes aléatoires sont irréductibles.
Toutefois cette distinction n'est pas si claire car elle peut dépendre du point de vue et des buts : l'incertitude sur la durée de vie d'un composant, si elle vous est fournie, est à considérer comme une incertitude aléatoire, mais si vous êtes le constructeur du dit composant, vous pouvez choisir de l'utiliser ainsi ou de lancer un processus de R&D pour améliorer le processus de fabrication et tenter de réduire cette dernière. Le coût acceptable (économique, temporel, structurel...) de la réduction rentre souvent en compte.


