Documentation
/ Guide méthodologique
: 
Abstract
This documentation is introducing the theoretical basics upon which the Uranie platform (based on Uranie v4.10.0), has been developed at CEA/DES. Since this platform is designed for uncertainty propagation, sensitivity analysis and surrogate model generation, the main methods which have been implemented are introduced and discussed. This document is however not made to give a complete overview of the methodology but more to open the scope of the reader by largely relying on a list of references, without getting to attached on the structure of the Uranie platform itself.
Table of Contents
- I. Glossary
- II. Basic statistical elements
- III. The Sampler module
- IV. Generating surrogate models
- V. Sensitivity analysis
- VI. Dealing with optimisation issues
- VII. The Calibration module
- VIII. The Uncertainty modeler module
- References
List of Figures
- II.1. Principle of the truncated PDF generation (right-hand side) from the orginal one (left-hand side).
- II.2. Example of PDF, CDF and inverse CDF for Uniform distribution.
- II.3. Example of PDF, CDF and inverse CDF for LogUniform distributions.
- II.4. Example of PDF, CDF and inverse CDF for Triangular distributions.
- II.5. Example of PDF, CDF and inverse CDF for Logtriangular distributions.
- II.6. Example of PDF, CDF and inverse CDF for Normal distributions.
- II.7. Example of PDF, CDF and inverse CDF for LogNormal distributions.
- II.8. Example of PDF, CDF and inverse CDF for Trapezium distributions.
- II.9. Example of PDF, CDF and inverse CDF for UniformByParts distributions.
- II.10. Example of PDF, CDF and inverse CDF for Exponential distributions.
- II.11. Example of PDF, CDF and inverse CDF for Cauchy distributions.
- II.12. Example of PDF, CDF and inverse CDF for GumbelMax distributions.
- II.13. Example of PDF, CDF and inverse CDF for Weibull distributions.
- II.14. Example of PDF, CDF and inverse CDF for Beta distributions.
- II.15. Example of PDF, CDF and inverse CDF for GenPareto distributions.
- II.16. Example of PDF, CDF and inverse CDF for Gamma distributions.
- II.17. Example of PDF, CDF and inverse CDF for InvGamma distributions.
- II.18. Example of PDF, CDF and inverse CDF for Student distribution.
- II.19. Example of PDF, CDF and inverse CDF for generalized normal distributions.
- II.20. Example of PDF, CDF and inverse CDF for a composed distribution made out of three normal distributions with respective weights.
- II.21. Illustration of the results of 100000 quantile determinations, applied to a reduced centered gaussian distribution, comparing the usual and Wilks methods. The number of points in the reduced centered gaussian distribution is varied, as well as the confidence level.
- III.1. Schematic view of the input/output relation through a code
- III.2. Comparison of the two sampling methods SRS (left) and LHS (right) with samples of size 8.
- III.3. Comparison of deterministic design-of-experiments obtained using either SRS (left) or LHS (right) algorithm, when having two independent random variables (uniform and normal one)
- III.4. Transformation of a classical LHS (left) to its corresponding maximin LHS (right) when considering a problem with two uniform distributions between 0 and 1.
- III.5. Matrix of distribution of three uniformly distributed variables on which three linear constraints are applied. The diagonal are the marginal distributions while the off-diagonal are the two-by-two scatter plots.
- III.6. Comparison of both quasi Monte-Carlo sequences with both LHS and SRS sampling when dealing with two uniform variables.
- III.7. Comparison of design-of-experiments made with Petras algorithm, using different level values, when dealing with two uniform variables.
- IV.1. Sketch of the evolution of the bias, the variance and their sum, as a function of the complexity of the model.
- IV.2. Sketches of under-trained (left), over-trained (middle) and properly trained (right) surrogate models, given that the black points show the training database, while the yellow ones show the testing database
- IV.3. Evolution of the different kinds of error used to determine when does one start to over-train a model
- IV.4. Schematical view of the projection of the original value from the code onto the subspace spanned by the column of H (in blue).
- IV.5. Schematic view of the Nisp methodology
- IV.6. Schematic description of a formal neuron, as seen in McCulloch and Pitts [McCulloch1943].
- IV.7. Example of transfer functions: the hyperbolic tangent (left) and the logistical one (right)
- IV.8. Schematic description of the working flow of an artificial neural network as used in Uranie
- IV.9. Influence of the variance parameter in the Matern function once fix at 0.5, 1 and 2 (from left to right). The correlation length is set to 1 while the smoothness is set to 3/2.
- IV.10. Influence of the correlation length parameter in the Matern function once fix at 0.5, 1 and 2 (from left to right). The variance is set to 1 while the smoothness is set to 3/2.
- IV.11. Influence of the smoothness parameter in the Matern function once fix at 0.5, 1.5 and 2.5 (from left to right). Both the variance and the correlation length are set to 1.
- IV.12. Evolution of the different covariance functions implemented in Uranie.
- IV.13. Example of kriging method applied on a simple uni-dimensional function, with a training site of six points, and tested on a basis of about hundred points, with either a gaussian correlation function (left) or a matern3/2 one (right).
- IV.14. Schematic description of the kriging procedure as done within Uranie
- V.1. Schematic view of two trajectories drawn randomly in the discretised hyper-volume (with p=6) for two different values of the elementary variation (the optimal one in black and the smallest one in pink, as detailed on the figure itself).
- VI.1. Naive example of an imaginary optimisation case relying on two objectives that only depend on a single input variable.
- VI.2. Description of the children production process in the Uranie implementation of the genetic algorithm
- VI.3. Comparison of two Pareto sets (left) and fronts (right) from vizir (blue) and MOEAD (ref) when the hollow bar case is studied with very low number of points, i.e. about 20 (simulating higher dimensions).
List of Tables
- II.1. List of Uranie classes representing the probability laws
- III.1. Proposed list of parameters value for simulated annealing algorithm, depending on the number of points
requested (
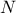 ) and the number of
inputs under consideration (
) and the number of
inputs under consideration (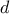 )
) - IV.1. List of best adapted polynomial-basis to develop the corresponding stochastic law
List of Equations
- II.2. General form of a SVD
- III.1. Covariance and correlation between two variables
- III.2. Simple correlation / de-correlation principle
- III.3. General form of a Cholesky decomposition with lower triangular matrix
- IV.1. Training database quality criteria definition
- IV.2. Validation database predictivity criterion definition
- IV.3. Leave-one-out quality criteria definition
- IV.4. Chaos polynomial function
- IV.5. polynomial chaos decomposition
- IV.6. General Matern function
- IV.7. Best estimate and its conditional variance for a single new location.
- IV.8. Best estimates and their covariance matrix, for a set of new locations.
- V.1. Linear model definition
- V.2. First order sensitivity index
- V.3. Total order sensitivity index
- V.5. Schematic view of the Sobol method
- V.6. Expectation and variance of output in Fourier space
- V.7. Fourier coefficient definition
- VII.4. Log-likelihood formula for a normally-distributed residue without homoscedasticity hypothesis
- VIII.1. Relation between multipliers and CIRCE parameters.



