Documentation
/ Guide méthodologique
: 
The deterministic samplings can produce design-of-experiments with well defined properties, that can be very useful in specific cases such as:
to cover at best the space of the input variables
to explore the extreme cases
to study combined or non-linearity effect
There are two kinds of quasi Monte-Carlo sampling methods implemented in Uranie: the regular ones and the sparse grid ones. On the first hand, the former can be generated using two different sequences:
Sequences of Sobol [SOBOL196786]
Sequences of Halton [HaltonSeq64]
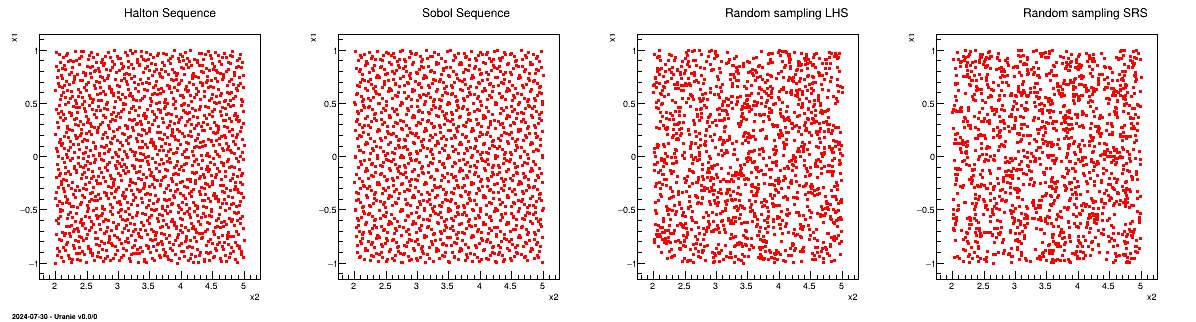
Figure III.6 shows a comparison of the design-of-experiments obtained with both sequences, along with the ones produced with a basic stochastic sampling, following the LHS and SRS "recipes", all when dealing with two uniform variables. The coverage is clearly more regular in the case of quasi Monte-Carlo sequences which is the origin of their name: low-discrepancy sequences. There are plenty definitions for the notion of discrepancy (see litterature for them) but they all quantify how close the sequence is to a perfect equidistribution of points.
Figure III.6. Comparison of both quasi Monte-Carlo sequences with both LHS and SRS sampling when dealing with two uniform variables.
 |
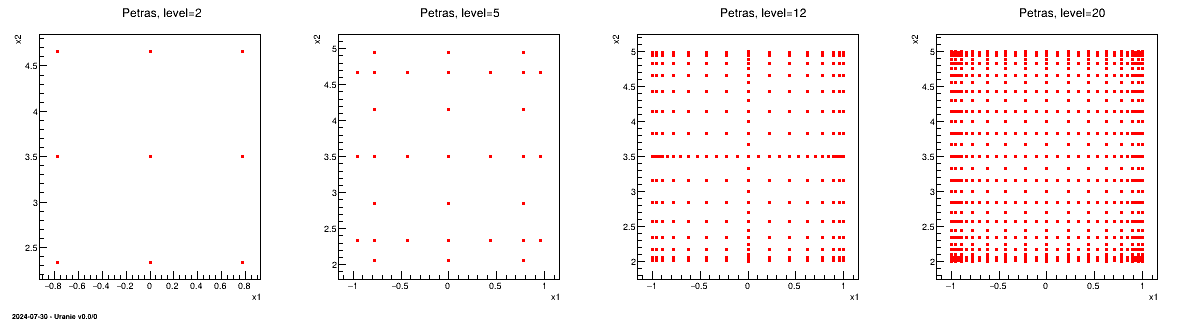
On the other hand, the sparse grid sampling can be very useful for integration purposes and can be used in some of the meta-modelling definition, see, for instance, in Section IV.3.2.2. In Uranie we can used the Petras algorithm [Petras2001] to produce these sparse grids, shown for different levels in Figure III.7, that can be compared to regular algorithms ones in Figure III.6 (in both cases, the problem is described with two uniform variables).
Figure III.7. Comparison of design-of-experiments made with Petras algorithm, using different level values, when dealing with two uniform variables.
 |






