Documentation / Methodological guide :

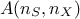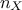When using the linear regression, one assumes that there is only one output variable and at least one input variable. The data from the training database are stored here in a matrix where is the number of elements in the set and is the number of input variables to be used. The idea is to write any output as 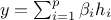, where are the regression coefficients and 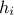, are the regressors: 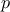simple functions depending on one or more input variables^[7] that will be the new basis for the linear regression. A classical simple case is to have 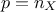and .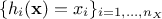

The regressor matrix is then constructed as 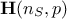and is filled with

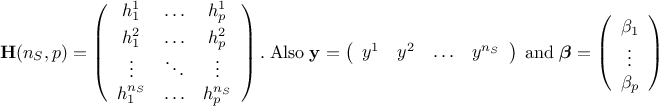
In the case where the number of points () is greater than the number of input variables (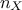), this estimation is just a minimisation of 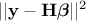which leads to the general form of the solution 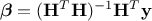. From this, the estimated values of the output from the regression are computed as 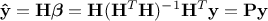, if one calls .

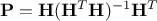As a result, a vector of parameters is computed and used to re-estimate the output parameter value. Few quality criteria are also computed, such as 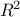and the adjusted one 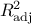. There is an interesting interpretation of the 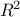criteria, in the specific case of a linear regression, coming from the previously introduced matrix 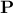, once considered as a projection matrix. It is indeed symmetrical and the following relation holds 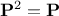, so the estimation 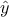by the linear regression is a orthogonal projection of 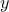onto the subspace 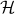spanned by the column of . 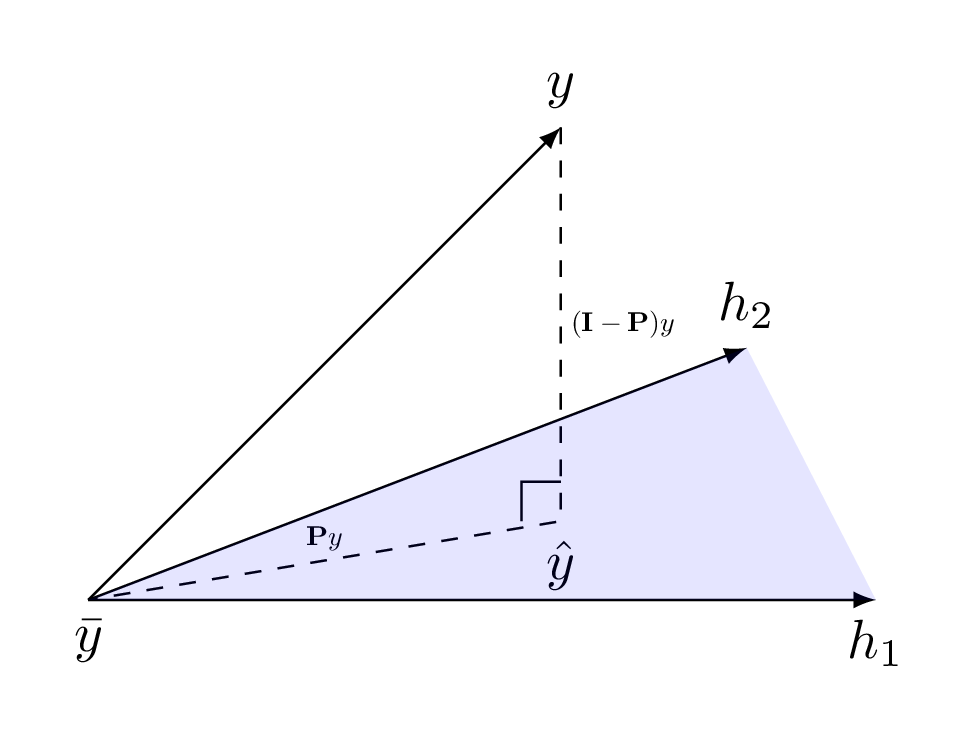This is depicted in Figure IV.4 and it shows that the variance, 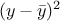can be decomposed into its component explained by the model 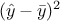and the residual part, 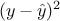. From this, the formula in Equation IV.1 can be also written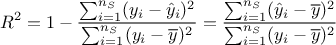

Figure IV.4. Schematical view of the projection of the original value from the code onto the subspace spanned by the column of H (in blue).

For theoretical completeness, in most cases, the matrix 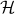is decomposed following a Singular Value Decomposition (SVD) such as 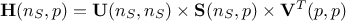. In this context 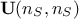and 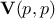are orthogonal matrices and 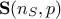is a diagonal matrix (that can also be stored as a singular values vector 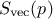). The diagonal matrix always exists, assuming that the number of samples is greater than the number of inputs (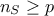). This has two main advantages the first one being that there is no matrix inversion to be performed, which implies that this procedure is more robust. The second advantage is when considering the 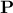matrix that links directly the output variable and its estimation through the surrogate model: it can now simply be written as . 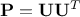This is highly practical once one knows that this matrix is used to compute the Leave-One-Out uncertainty, only considering its diagonal component.