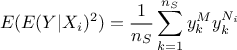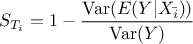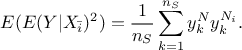Documentation
/ Methodological guide
: 
The Sobol method is a Monte-Carlo based estimation that provides the first and total order sensitivity indices at the
cost of requiring a total of 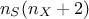 code assessments. In order to produce these results, a design-of-experiments must be produced, whom size
(
code assessments. In order to produce these results, a design-of-experiments must be produced, whom size
( ) has to be precised by the
user. Instead of generating one design-of-experiments with the requested properties, the program generates actually twice as many
data points, split in two different matrices that one could call
) has to be precised by the
user. Instead of generating one design-of-experiments with the requested properties, the program generates actually twice as many
data points, split in two different matrices that one could call 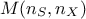 and
and 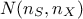 (both matrices are different and independent random samplings). The method is
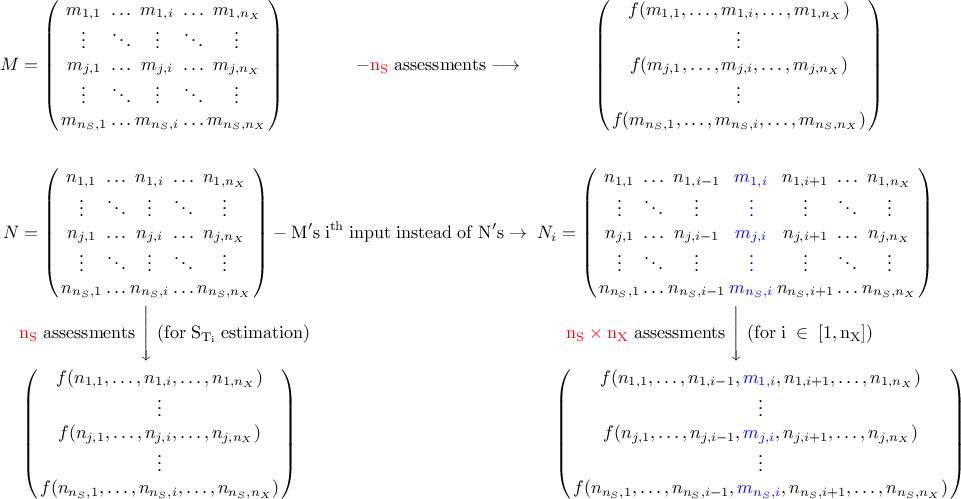
detailed in the following paragraph, separately for the first and total order indices, but a schematic view can be
found at the end in Equation V.5.
(both matrices are different and independent random samplings). The method is
detailed in the following paragraph, separately for the first and total order indices, but a schematic view can be
found at the end in Equation V.5.
The first step is to compute the first order sensitivity index, whose definition has been given in Equation V.2. This estimation is based on the measurement of the numerator, 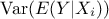 , which can be written
, which can be written
 from the definition of variance. Since the second part of previous formula is equivalent to the
output expectation, the needed inputs to get the first order indices are:
from the definition of variance. Since the second part of previous formula is equivalent to the
output expectation, the needed inputs to get the first order indices are: 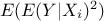 ,
, 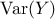 and
and 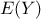 . The method discussed in the following paragraphs and illustrated by Equation V.5 is called the pick-and-freeze method. The matrix
. The method discussed in the following paragraphs and illustrated by Equation V.5 is called the pick-and-freeze method. The matrix 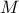 is passed to the code and
is passed to the code and  assessment are done to get a vector of outputs (this is
shown by the first line of Equation V.5). From this, the output properties can easily be
estimated, leaving the first term only to be measured. In order to estimate it for the i-Th input variable, one needs
to have two different random sampling with the i-Th component (to satisfy the conditional character of the
expectation to be squared). This is where the second matrix
assessment are done to get a vector of outputs (this is
shown by the first line of Equation V.5). From this, the output properties can easily be
estimated, leaving the first term only to be measured. In order to estimate it for the i-Th input variable, one needs
to have two different random sampling with the i-Th component (to satisfy the conditional character of the
expectation to be squared). This is where the second matrix 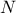 is used: its i-Th column is replaced by the
is used: its i-Th column is replaced by the 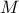 's one (peek), creating an new
's one (peek), creating an new 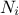 matrix. The last term to be estimated can be computed
as
matrix. The last term to be estimated can be computed
as
(the mathematical
development leading to this formula can be found in many references). This step, whose total cost is 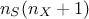 code assessments, is shown by
the second line and the right-part of the third line in Equation V.5 (following the arrows).
code assessments, is shown by
the second line and the right-part of the third line in Equation V.5 (following the arrows).
Finally the total order indices are computed starting from the second part of Equation V.3. This second part can also be written as
which looks very much alike Equation V.2 used to compute the first order but
instead of a condition on having 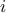 known (frozen), it is the exact opposite: the condition is to freeze everything but
known (frozen), it is the exact opposite: the condition is to freeze everything but
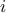 . This is easily doable as this is
the only difference between the
. This is easily doable as this is
the only difference between the 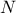 and
and 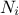 matrices. Following the
same recipe as for the first order, only the
matrices. Following the
same recipe as for the first order, only the 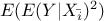 has to be computed with the following formula:
has to be computed with the following formula:
The compulsory step is so to pass the
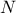 matrix to the code, leading to
matrix to the code, leading to
 code assessments, as shown in
Equation V.5 by the left part of the third line.
code assessments, as shown in
Equation V.5 by the left part of the third line.
This method is, in Uranie, said to be "� la Saltelli" in contrast with the other implementation (previously
used as default) which is said to be "� la Sobol". The difference between the two being the number of assessment used
to get a certain precision: for the same results, the implementation "� la Sobol" was requesting 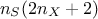 and was offering more
numerical results as five algorithms were used. The new implementation "� la Saltelli" requests only
and was offering more
numerical results as five algorithms were used. The new implementation "� la Saltelli" requests only 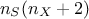 estimation but only three
algorithms are run. This is summarised as follow where the bold name is the default stored in
--first-- and --total--:
estimation but only three
algorithms are run. This is summarised as follow where the bold name is the default stored in
--first-- and --total--:
- a la Saltelli
First order: Saltelli02 [Saltelli02], Sumo10 [Monod06], Martinez11 [Martinez11]
Total order: Homma96 [Homma96], Sumo10 [Monod06], Martinez11 [Martinez11]
- a la Sobol
First order: Sobol93 [Sobol93], Saltelli02 [Saltelli02], Jansen99 [Jansen99], Sumo10 [Monod06], Martinez11 [Martinez11]
Total order: Homma96 [Homma96], Saltelli02 [Saltelli02], Jansen99 [Jansen99], Sumo10 [Monod06], Martinez11 [Martinez11]
Tip
The Martinez11 algorithm is the recommended one, as it provides an estimation of the 95% confidence interval for every coefficient determined.