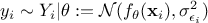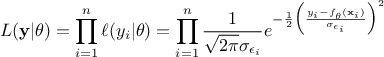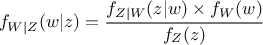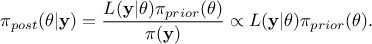Documentation
/ Methodological guide
: 
| Chapter VII. The Calibration module | ||
|---|---|---|
 |  | |
Table of Contents
This section presents different calibration methods that are provided to help get a correct estimation of the parameters of a model with respect to data (either from experiment or from simulation). The methods implemented in Uranie are going from the point estimation to more advanced Bayesian techniques and they mainly differ from the hypothesis that can be used.
In general, a calibration procedure will request an input datasets meaning an existing set of
elements (either resulting from simulations or experiments). This ensemble (of size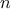 
) can be written as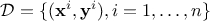 
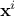is the i-Th input vector which can be written as 
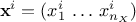while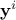 
is the i-Th
output vector which can be written as 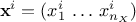.These data will be compared to model predictions, the model being a
mathematical function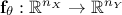 
. From now on and unless otherwise specified (for
distance definition for instance, see Section VII.1.1) the dimension of the output is
set to 1 (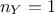
) which means
that the reference observations and the predictions of the model are scalars (the observation will then be written
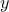and the prediction of the model
).
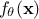On top of the input vector, already introduced previously, the model depends also on a parameter vector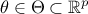 
which is constant but
unknown. The model is deterministic, meaning that 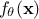is constant once both 
and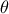 
are fixed. In the rest of this documentation, a given set of parameter value
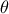is called a configuration.
The standard hypothesis for probabilistic calibration is that the observations differ from the the predictions of the model by a certain amount which is supposed to be a random variable as
where
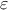is a random
variable whose expectation is equal to 0 and which is called residue. This variable represents the
deviation between the model prediction and the observation under investigation. It might arise from two possible
origins which are not mutually exclusive:
experimental: affecting the observations. For a given observation, it could be written
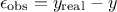
modelling: the chosen model
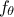is intrinsically not correct. This contribution could be written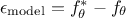 
As the ultimate goal is to have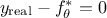 
, injecting back the two contributions discussed above, this translates
back to equation Equation VII.1, only breaking down: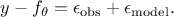 
The rest of this section introduces two important discussions that will be referenced throughout this module:
the distance between observations and the predictions of the models, in Section VII.1.1;
the theoretical background and hypotheses (linear assumption, concept of prior and posterior distributions, the Bayes formulation...) in Section VII.1.2.
The former is simply the way to obtain statistic over the 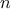samples of the reference observations when comparing them to a set of parameters and how
these statistics are computed when the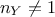 
. The latter is a general introduction, partly reminding elements already introduced in other
sections and discussing some assumptions and theoretical inputs needed to understand the methods discussed later-on.
On top of this description, there are several predefined calibration procedures proposed in the Uranie platform:
The minimisation, discussed in Section VII.2
The linear Bayesian estimation, discussed in Section VII.3
The ABC approaches, discussed in Section VII.4
The Markov-chain Monte-Carlo sampling, discussed in Section VII.5
There are many ways to quantify the agreement of the observations (our references) with the predictions of the model
given a provided vector of parameter 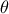. As a reminder, this step has to be run every time a new vector of parameter 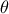is under investigation which means that the code
(or function) should be run 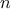times
for each new parameter vector.
Starting from the formalism introduced above, many different distance functions can be computed. Given the fact that
the number of variable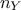 
used to
perform the calibration can be different than 1, one might also need variable weight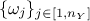 
that might
be used to ponderate the contribution of every variable with respect to the others. Given this, here is a
non-exhaustive list of distance functions:
L1 distance function (sometimes called Manhattan distance):
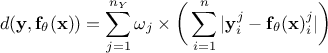
Least square distance function:
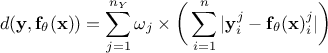
Relative least square distance function:
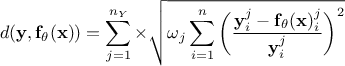
Weighted least square distance function:
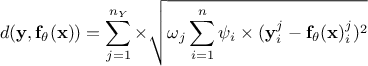where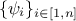 
are weights used to ponderate each
and every observations with respect to the others.
Mahalanobis distance function:
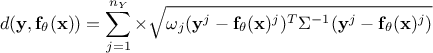where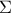 
is the covariance matrix of the observations.
These definitions are not orthogonal, indeed if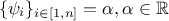 
, then the least-square
function is equivalent to the weighted least-square one. This situation is concrete as it can correspond to the case
where the least-square estimation is weighted with an uncertainty affecting the observations, assuming the uncertainty
is constant throughout the data (meaning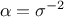 
). This is called the Homoscedasticity
hypothesis and it is important for the linear case, as discussed later-on.
One can also compare the relative and weighted least-square, if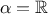 
and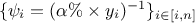 
these two
forms become equivalent (the relative least-square is useful when uncertainty on observations is
multiplicative). Finally if one assumes that the covariance matrix of the observations is the identity (meaning
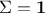), the
Mahalanobis distance is equivalent to the least-square distance.
Warning
It is important to stress something here : it might seem natural to think that the lower the distance is, the closest to the real values our parameters are. Bearing this in mind would mean thinking that "having a null distance" is the ultimate target of calibration, which is actually dangerous. As for the general discussion in Chapter IV, the risk could be to overfit the set of parameters by "learning" just the set of observations at our disposal as the "truth", not considering that the residue (introduced in Equation VII.1) might be here to introduce observation uncertainties. In this case, knowing the value of the uncertainty on the observations, the ultimate target of the calibration might be to get the best agreement of observations and model predictions within the uncertainty models, which can be translated into a distribution of the reduced-residue (that would be something like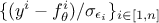
in a scalar cases) behaving like a centred
reduced Gaussian distribution.
VVUQ is a known acronym standing for "Verification, Validation and Uncertainty Quantification". Within this framework, the calibration procedure of a model, also called sometimes "Inverse problem" [Tarantola2005] or "data assimilation" [Asch2016] depending on the hypotheses and the context, is an important step of uncertainty quantification. This step should not be confused with validation, even if both procedures are based on comparison between reference data and model predictions, their definition is recalled here [trucano2006calibration]
- validation:
process of determining the degree to which a model is an accurate representation of the real world from the perspective of the intended uses of the model.
- calibration:
process of improving the agreement of a code calculation or set of code calculations with respect to a chosen set of benchmarks through the adjustment of parameters implemented in the code.
The underlying question to validation is "What is the confidence level that can be granted to the model given the difference seen between the predictions and physical reality ?" while the underlying question of calibration is "Given the chosen model, what parameter's value minimise the difference between a set of observations and its predictions, under the chosen statistical hypotheses ?".
In can happen sometimes that a calibration problem allows an infinity of equivalent solutions
[Hansen1998], which is possible for instance when the chosen model 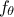depends explicitly on an operation of two
parameters. The simplest example would be to have a model 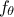depending only on two parameters through the difference 
. In this peculiar case,
every couple of parameters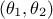 
that would lead to the same difference would provide the exact same model
prediction, which means that it is impossible to disentangle these solutions. This issue, also known as
identifiability of the parameters is crucial as one needs to think at the way our chosen is parameterised
[walter1997identification].
Defining a calibration analysis consists in several important steps:
Precise the ensemble of observations that will be used as reference;
Precise the model that is supposed to fairly describe the real world;
Define the parameters to be analysed (either by defining the a priori laws or at least by setting a range). This step is the moment where caution has to be taken on the identifiability issue.
Choose the method used to calibrate the parameters.
Choose the distance function used to quantify the distance between the observations and the predictions of the model.
The least-square distance function introduced in Section VII.1.1 is very classically used when considering calibration issue. This is true whether one is considering calibration within a statistical approach or not (see the discussion on uncertainty sources in Section VII.1). The importance of the least-square approach can be understood by adding an extra hypothesis on the residue defined previously. If one considers that the residue is normally distributed, it implies that one can write
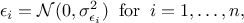
where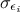 
can quantify both sources
of uncertainty and whose values are supposed known. The formula above can be used to transform equation Equation VII.1 into (setting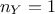 
for simplicity):
This particular case is very interesting, as from equation Equation VII.2 it
becomes possible to write down the probability of the observation set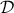 
as the product of all its component probability which can
be summarised as such:
A logical approach is to consider than the fact the datasets 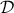has been observed, means that the probability of this collection of
observations is highly probable. The probability defined in equation Equation VII.3 can then be
maximised by varying 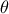in
order to get its most probable values. This is called the Maximum Likelihood Estimation (MLE) and maximising the
likelihood is equivalent to minimise the logarithm of the likelihood which can be written as:
Equation VII.4. Log-likelihood formula for a normally-distributed residue without homoscedasticity hypothesis
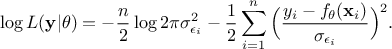
The first part of the right-hand side is independent
of 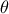which means that
minimising the log-likelihood is basically focusing on the second part of the right-hand size which is basically the
weighted least-square distance with the weights set to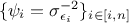 
.
Finally on the way to get an estimation of the parameters in this case, it depends on the underlying hypotheses of the model, and this discussion is postponed to another section (this is discussed in Section VII.2). More details on least-square concepts can be found in many references, such as [Borck1996, Hansen2013].
The probability for an event to happen can be seen as the limit of its occurrence rate or as the quantification of a
personal judgement or opinion as for its realisation. This is a difference in interpretation that usually split the
frequentist and the Bayesian. For a simple illustration one can flip a coin : the probability of getting head,
denoted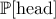 
is either the average result of a very large number of experiments (this definition being very
factual but whose value depends highly on the size of the set of experiments) or the intimate conviction that the
coin is well-balanced or not (which is basically an a priori opinion that might be based on
observations, or not).
Lets call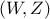 
a
random vector with a joined probability density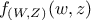 
and marginal densities written as 
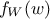and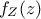 
. From there, the Bayes rules states that:
where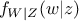 
(respectively 
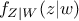) is the conditional probability density of
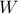knowing that 
has been realised (and vice-versa
respectively). These laws are called conditional laws.
Getting back to our formalism introduced previously, using equation Equation VII.5 implies that
the probability density of the random variable 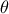given our observations, which is called posterior
distribution, can be expressed as
In this equation,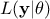 
represents the conditional probability of the observations knowing the
values of ,
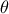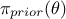is
the a priori probability density of 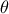, often referred to as prior, 
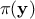is the marginal likelihood
of the observations, which is constant in our scope (as it does not depend on the values of 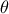but only on its prior, as 
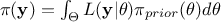, it consists only in a normalisation factor).
The prior law is said to be proper when one can integrate it, and improper
otherwise. It is conventional to simplify the notations, by writing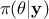 
instead of 
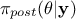and
also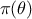 
instead of
.
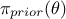The choice of the prior is a crucial step when defining the calibration procedure and it must rely on physical
constraints of the problem, expert judgement and any other relevant information. If one of these are available or
reliable, it is still possible to use non-informative priors for which the calibration will only use the data as
inputs. One can find more discussions on non-informative prior here
[jeffreys1946invariant,bioche2015approximation].
| | | |
| VI.2. Multicriteria optimisation |  | VII.2. Using minimisation techniques |