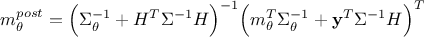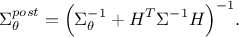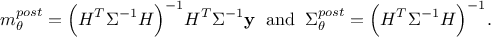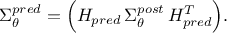Documentation / Guide méthodologique :

This method consists mainly in the analytical formulation of the posterior distribution when the hypotheses on the prior are well set: the problem can be considered linear and the prior distributions are normally distributed (or flat, this aspect being precised at the end of this section).

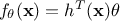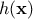In the specific case of a linear model, one can write then where is the regressor vector. This way of writing the model can include an "hidden virtual" 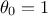whose purpose is to integrate a constant term into the regression (to describe a pedestal). Using the statistical approach introduced in Section VII.1, one can also define the covariance matrix of the residue which will be written hereafter as

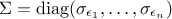
From there, one can construct the conception matrix 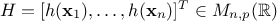whose columns are defining the sub-space onto which the model is projected. With a normal prior, which follows the form 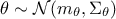the posterior is expected to be normal as well, meaning that it can be written 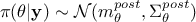where its parameters are expressed as

Equation VII.7. 

and

Equation VII.8. 

Actually, one can also use, as already introduced in Section VII.1.2.3, non-informative prior such as the Jeffrey's prior: it is an improper flat prior (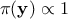) [bioche2015approximation], whose posterior distribution (in the linear case) is also Gaussian. For this prior, the parameters of the posterior are equivalent to the parameters of the posterior from a Gaussian prior, given in Equation VII.7 and Equation VII.8 only removing all reference to 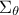, as shown here:

Equation VII.9. 

This final form is the results expected and obtained when only considering linear regression of the weighted least-squares approach [Fry2010].

VII.3.1. Prediction values

Once both the posterior parameter values and covariances are estimated, it is possible to get a prediction for a set of data not used to get the estimation. The central value of the prediction is easy to get, as for any other methods shown in this documentation, since one knows the model and can use the newly estimated posterior central values of the parameters.

What's new is the fact that a variance can be estimated as well for the predicted central value using the posterior covariance matrix of the parameters, 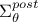, already introduced in Equation VII.8. This variance is the variance for every new estimated points coming from the uncertainty of the parameters, and it is contained in the covariance matrix 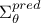whose dimension is 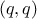, where 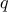is the size sample under consideration. To get the estimation one needs the new conception matrix 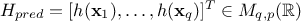which leads to

Equation VII.10.