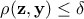Documentation
/ Guide méthodologique
: 
This sections is discussing methods gathered below the ABC acronym, which stands for Approximation Bayesian Computation. The idea behind these methods is to perform Bayesian inference without having to explicitly evaluate the model likelihood function, which is why these methods are also referred to as likelihood-free algorithms [wilkinson2013approximate].
As a reminder of what's discussed in further details in Section VII.1.2.3, the principle of the Bayesian approach is recap
in the equation 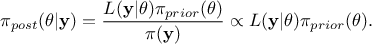 where
where 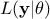 represents the conditional probability of the observations knowing the values of
represents the conditional probability of the observations knowing the values of 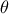 ,
, 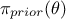 is the a
priori probability density of
is the a
priori probability density of 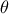 (the prior) and
(the prior) and 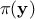 is the marginal likelihood of the observations, which is
constant here. It does, indeed, not depend on the values of
is the marginal likelihood of the observations, which is
constant here. It does, indeed, not depend on the values of 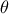 but only on its prior, as
but only on its prior, as 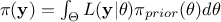 which makes this a normalisation factor.
which makes this a normalisation factor.
The rejection ABC is the simplest possible version of the ABC approach. Its prehistory genesis was stated in the
eighties [rubin1984bayesianly] and it is possible to see a nice introduction of the rejection
algorithm as originally applied to a problem with a finite countable set  of values in [marin2012approximate]. In
this specific case, it only consisted in two random drawing: the parameter's value according to their prior then the
model prediction according to the parameter's value just drawn. If the results was the element of the reference data
set, the configuration was kept.
of values in [marin2012approximate]. In
this specific case, it only consisted in two random drawing: the parameter's value according to their prior then the
model prediction according to the parameter's value just drawn. If the results was the element of the reference data
set, the configuration was kept.
Things are getting a bit more tricky when considering continuous sample spaces are there is no such thing are strict equality when considering stochastic behaviour (without even discussing the numerical issues that have to arise at some points). This implies the need for two important concepts
a distance measure on the output space, denoted
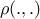 ;
;
a tolerance determining the accuracy of the algorithm and denoted
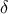 .
.
Unlike the simpler discrete case quickly introduced above where the aim is to have strict equality between the predictions and the reference data, here the accepted configurations would be those fulfilling the following condition
where 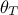 is the configuration under study draw
following the prior
is the configuration under study draw
following the prior 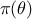 and
and  is the model predictions estimated from
is the model predictions estimated from 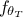 once run on the reference datasets. This was firstly used in the
late nineties, as can be seen in [pritchard1999population].
once run on the reference datasets. This was firstly used in the
late nineties, as can be seen in [pritchard1999population].
Warning
A peculiar attention has be to taken to the way the model is defined : one should recall that the uncertainty model is defined on the residue, as stated in Equation VII.1 and that residue is usually considered normally-distributed Equation VII.2. Disregarding the origin of this residue, as discussed in Section VII.1, if the model one is providing is deterministic, the calibration will focus on a single realisation of the observation without uncertainty consideration. In this case, the model prediction must be modified to include a noise representative of the residue hypotheses [van2018taking].
This methodology shows that accepted configurations are not really taken out of the true posterior distribution
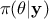 but they're coming from an approximation of it that can be written
but they're coming from an approximation of it that can be written 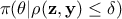 . Two interesting asymptotic regime can be emphasised:
. Two interesting asymptotic regime can be emphasised:
when
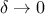 : the algorithm is exact and is leading to the real
: the algorithm is exact and is leading to the real 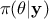 ;
;
when
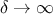 : this algorithm does not use information from the reference datasets and gives back the
original prior
: this algorithm does not use information from the reference datasets and gives back the
original prior 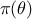 instead.
instead.
There are many different version of this kind of algorithm, among which one could find an extra step using summary
statistic 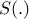 to project
both
to project
both  and
and
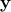 onto a lower
dimensional space. In this version, the configurations kept are drawn from
onto a lower
dimensional space. In this version, the configurations kept are drawn from 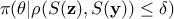 .
.
Finally another possible way to select the best representative sub-sample might be by using a percentile of the
analysed and computed set of configurations. Although, mainly recommended for high-dimension case (meaning when
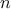 is become large), this solution
might works as long as one keep an eye on the residue distribution provided by the a posteriori
estimated parameters. Indeed, if no threshold is chosen but a percentile is used, the requested number of
configurations will always been brought at the end, but the only way to check whether the uncertainty hypotheses were
correct is to look at how close the predictions have become for the full reference datasets.
is become large), this solution
might works as long as one keep an eye on the residue distribution provided by the a posteriori
estimated parameters. Indeed, if no threshold is chosen but a percentile is used, the requested number of
configurations will always been brought at the end, but the only way to check whether the uncertainty hypotheses were
correct is to look at how close the predictions have become for the full reference datasets.