Documentation / User's manual in C++ :

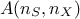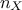When using the TLinearRegression class, one assumes that there is only one output variable and at least one input variable. The data from the training database, shown in Figure V.1, are stored here in a matrix where is the number of elements in the set and is the number of input variables to be used. The idea is to write any output as 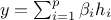, where are the regression coefficients and 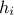, are the regressors: 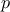simple functions depending on one or more input variables^[3] that will be the new basis for the linear regression. A classical simple case is to have 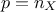and 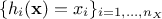. The chosen regressors are precised during the construction of the TLinearRegression object, as it takes the TDataServer as first input, a string encoding the regressors to be used and a string encoding the output name.

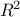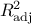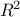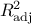As a result, a vector of parameters is computed and used to re-estimate the output parameter value. Few quality criteria are also computed, such as and the adjusted one (the value of tends to increase when additional variables are added to the regression equation even if these variables do not significantly improve the regression, this is why the adjusted version, has been created, see [metho] for a discussion on these criteria).

Here is an usage-example of the TLinearRegression class:

{
  TDataServer * tds = new TDataServer();
  tds->fileDataRead("flowrate_sampler_launcher_500.dat"); // Read the database

  TLinearRegression *tlin = new TLinearRegression(tds, "rw:r:tu:tl:hu:hl:l:kw", "yhat"); // Create the linear regression
  tlin->estimate(); // Estimate the parameters

  cout << " ** R2[" << tlin->getR2() << "] R2A[" << tlin->getR2Adjusted() << "] QR2[" << tlin->getQ2() << "]" << endl; 

  tlin->exportFunction("c++", "myASCIIFile", "myFunction");
  }

It results to this output:

 ** R2[0.948985] R2A[0.948154] QR2[0.946835]