Documentation
/ Manuel utilisateur en C++
: 
The Wrapper of the Anisp library is a tool allowing to access to Anisp functionalities from Uranie platform. At present, the main features are detailed below.
The Anisp library models uncertainties. It allows to use spectral methods based on polynomial chaos in modelling and propagation studies and adaptive numerical integration if uncertainties arise in the numerical models. Concretely, the Anisp library uses adaptive numerical integration to compute an adapted polynomial expansion with less simulations and a smaller polynomial basis. The steps of an uncertainty analysis by using the Anisp methodology are the following:
Specification of the uncertain parameters
 ,
,
Creation of the
TAnispobject and specification of the Anisp parameters (tolerance, maximum number of simulations, ...),The building of stochastic variables associated
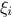 , the building of an adaptive sampling and building of an adapted chaos
polynomial are automatically handled by the Anisp method,
, the building of an adaptive sampling and building of an adapted chaos
polynomial are automatically handled by the Anisp method,
Uncertainty and sensitivity analysis.
The functionality of Anisp, accessible from Uranie, are explained following a scenario based on an usual example, the Ishigami test case. This scenario is decomposed according to the steps described below.
First, it is necessary to build a dataserver containing the uncertain parameters  . These parameters are represented by random variables which
follow one of these statistical laws:
. These parameters are represented by random variables which
follow one of these statistical laws:
Uniform law,
Normal law.
For other laws, it is necessary to use TAttributeFormula and to configure them from Uniform and
Normal laws.
Example 1:
Within the framework of our case-test example, we are going to build a TDataServer containing 3 attributes which follow a
uniform law on the interval [-π,+π].
TDataServer *tds = new TDataServer("tdsishigami", "Ex. Ishigami");
tds->addAttribute( new TUniformDistribution("x1", -1*TMath::Pi(), TMath::Pi()));
tds->addAttribute( new TUniformDistribution("x2", -1*TMath::Pi(), TMath::Pi()));
tds->addAttribute( new TUniformDistribution("x3", -1*TMath::Pi(), TMath::Pi()));
Example 2 (using a TAttributeFormula):
We are going to build a TDataServer containing 3 attributes, the first 2 follow a uniform law on the interval [-1/2,+1/2] and
the third is a TAttributeFormula. As a consequence 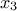 follows Log-Uniform on the interval [exp(-1/2),exp(+1/2)].
follows Log-Uniform on the interval [exp(-1/2),exp(+1/2)].
TDataServer *tdsVenise = new TDataServer("tdsVenise","Ex. Venise");
tdsVenise->addAttribute( new TUniformDistribution("x1", -0.5, 0.5));
tdsVenise->addAttribute( new TUniformDistribution("x2", -0.5, 0.5));
tdsVenise->addAttribute( new TAttributeFormula("x3","TMath::Exp(x2)")); Warning
If a TAttributeFormula uses 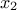 to configure
to configure 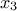 then
then 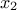 must not be an argument of the
must not be an argument of the TCode or the
TLauncherFunction used to launch computations.
Now, we create the TAnisp object by using one of the two constructors: TAnisp(TDataServer* ,const char *, TString, TString, Option_t *) and TAnisp(TDataServer* ,TCode *, Option_t *). The first constructor is when
we want to approximate a function (see TLauncherFunction) and the second when it's a numerical
code (see TCode and TLauncher).
Example:
In our example, we use the first constructor because Ishigami is an analytic function. The first
TString argument indicates the names and order (according to the TDataServer attributes) of the input
arguments for the function and the second TString the name of the output argument:
//Definition of the TAnisp object
TAnisp * tanisp = new TAnisp(tds, "FctIshigami","x1:x2:x3","Ishigami"); Warning
There must be only one output argument, this is one of the limitation of the Anisp method.
Now, we can specify some of the parameters of the Anisp method, if the defaults are not adapted to the case. The parameters we can specify are:
the tolerance of the integration algorithm: it determines the precision we want;
the maximum number of simulations: it stops the computations if it is exceeded;
the minimum level of interactions (kmin): it specifies the minimum level of interaction investigated, it must be inferior to the number of variables and it increases the initialisation number of simulations of the algorithm;
the greater index: maximum value in a dimension of a multi-index integration, it's value is limited to 6 in the case of a Normal variable;
the maximum number of multi-index integration: it is a memory criterion, it's default value is 5000;
the graphical output parameter: to set or unset the console and graphical outputs;
the maximum degree: it specify the maximum degree in a dimension for the polynomials;
the root of the names of the Anisp files: the Anisp library created several files, the user can specify the root of their names, "fichierAnisp_" is the default value.
For each of these parameters there is a method to set the value, in order: setTolerance,
setNumberMaxOfSimulations, setKMin,
setGreaterIndice, setMaxIndices, setlog,
setDegreeMax and setRootFilename.
There is also three methods which allow to set several parameters:
setAllAnispParametersmodifies all the parameters;setAnispParametersmodifies only some parameters: tolerance, kmin, number maximum of simulation, greater index, maximum indices and the graphical outputs parameter;setLightAnispParametersmodifies only the computation parameters: tolerance, kmin and number maximum of simulations.
Example:
//Tolerance of the algorithm
Double_t tol = 1.0E-2;
//Maximum number of simulations
Int_t max = 200;
//minimum level of interactions
Int_t kmin = 1;
//setting these parameters
tanisp->setLightAnispParameters(tol,kmin,max);
//root name
TString racine = TString("IshigamiAnisp_");
tanisp->setRootFilename(racine);
// set graphical outputs
tanisp->setlog(kTRUE);
The construction of the associated stochastic variables ξi, the generation of the adaptive
sampling and the adapted polynomial chaos expansion are automatically handled by the Anisp method. Once the
TAnisp object is created and new parameters set (if necessary), the user is left with the
runAnisp method of the class TAnisp.
Example:
//run of Anisp
tanisp->runAnisp();
After using the runAnisp method, it's possible for the user to set new parameters and then
restart the algorithm where it has stopped by using the method restartAnisp of the class
TAnisp.
Example:
//new parameters
tol = 1.0E-6; max = 1000; kmin = 2;
tanisp->setLightAnispParameters(tol,kmin,max);
//restart of Anisp
tanisp->restartAnisp(); Now, we can do the uncertainty and sensitivity analysis. With the Anisp library, we have access to the functionality of the Nisp library.
Indeed the TAnisp object create a TPolynomialChaos object during the
call of the runAnisp and restartAnisp methods. The user can then use
the getTPolynomialChaos method to get back the TPolynomialChaos object
and perform the uncertainty and sensitivity analysis by using the dedicated method of this class.
Another way is to use the exportFunction method which creates a C++ file containing the polynomial under the form of a C++ function. The user can then perform on it any statistical analysis.
Example:
//getting the TPolynomialChaos object
TPolynomialChaos * pc;
TPolynomialChaos P1(tanisp->getTPolynomialChaos());
pc = &P1;
//Uncertainty and sensitivity analysis using TPolynomialChaos functionality
cout<<endl;
cout<<"Mean = "<< pc->getMean(0)<< endl;
cout<<"Variance = "<< pc->getVariance(0)<< endl;
cout<<endl;
cout<<"First Order[1] = "<< pc->getIndexFirstOrder(0,0)<<endl;
cout<<"First Order[2] = "<< pc->getIndexFirstOrder(1,0)<<endl;
cout<<"First Order[3] = "<< pc->getIndexFirstOrder(2,0)<<endl;
cout<<endl;
cout<<"Total Order[1] = "<< pc->getIndexTotalOrder(0,0)<<endl;
cout<<"Total Order[2] = "<< pc->getIndexTotalOrder(1,0)<<endl;
cout<<"Total Order[3] = "<< pc->getIndexTotalOrder(2,0)<<endl;
cout<<endl;
cout<<"Ordered functionnal ANOVA"<<endl;
Double_t seuil = 0.98;
pc->getAnovaOrdered(seuil,0);
// Export of the polynomial in a C++ file
tanisp->exportFunction("c++","AnispIshigami.C","AnispIshigami"); 





