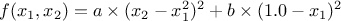Documentation
/ User's manual in C++
: 
The first optimisation type is the search for the optimum set of values of a function that takes
its values in 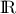 .
.
To illustrate the usage of the Optimizer module with (both analytic and computational) functions, we are going to use the Rosenbrock function from the literature [rosenbrock1960automatic].
The Rosenbrock function is widely used in optimisation libraries. It is a function of 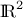 in
in 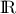 . It is defined, for two parameters {a, b} in
. It is defined, for two parameters {a, b} in 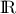 , by:
, by:
In the illustration below, the two parameters are set to: a = 10.0 and b = 1.0.
By analytic computation, it can be proved that the Rosenbrock function is minimum in (1, 1) for all the values of a and b, if parameters a and b are both positive.
The Rosenbrock function is defined in the file UserFunctions.C (in the macros folder
${URANIESYS}/share/uranie/macros) with the prototype:
void rosenbrock(Double_t *x, Double_t *y)Its content is as follow:
Also provided with Uranie comes an executable version of the Rosenbrock function. In this case, the Rosenbrock function is not an analytic function as described above anymore, but a computational code compiled with Uranie, that deals with input and output files.
Below are presented the available parameters of the rosenbrock executable (available in the
${URANIESYS}/bin folder):
Usage: rosenbrock [-d] [-v] [-k|-r] [file] -v: verbose mode -d: debug mode (prints most of its steps in order to debug the code in case of problem) -k: input file with keys [default is input_rosenbrock_with_keys.dat] -r: input file with only values in rows [default is input_rosenbrock_with_values_rows.dat] file: name of the input file, if different from the default name
- -v option allows to print some messages to know the state of the code
- -d option allows to give some intermediate values to users while executing rosenbrock, such as values read in input files, or to show steps or information in execution.
- -k options allow to simulate the launch of rosenbrock with data files of "key=value" format. If user does not specify an input file, rosenbrock will look for the input file input_rosenbrock_with_keys.dat whom "key=value" format is described below.
- -r option allows to simulate the launch of rosenbrock code with files with values in rows. The default input file is input_rosenbrock_with_values_rows.dat whom "values in rows" format is described below.
Note that the input file must contain at least two values, for the parameters x and y. Values for a and b can be omitted, in which case default values 10 and 1 will be respectively taken.
In this section are described the file formats the rosenbrock executable can read.
When used with the "-k" option, the rosenbrock executable takes its parameters from input files with format "key=value", where the keys are the variable names, i.e. x, y, a and b. By default, the file input_rosenbrock_with_keys.dat is taken as an input file, but if the user creates a new file, it must keep the same format. Below is the content of the default file, input_rosenbrock_with_keys.dat:
# # # inputfile for the \b rosenbrock code # \date mar jui 3 14:38:43 2007 # the two parameters # x = -1.20 ; y = 1.0 ; a = 10.0 ; b = 1.0 ;
As presented below, if the user does not want to specify the values for parameters a and b, the following file will produce the same result:
x = -1.20 ; y = 1.0 ;
When used with the "-r" option, the rosenbrock executable gets the parameters from input files where values are stored in a single row, in the following order: x, y, a and b. The default file is input_rosenbrock_with_values_rows.dat, which is taken if no file is specified. Below is the content of the default file, input_rosenbrock_with_values_rows.dat:
-1.20 1.0
The rosenbrock code generates two output files, in which are stored both input attributes and output
values:
_output_rosenbrock_with_values_rows_.dat: file with "row" format and with a header containing the names of the variables, and then their values:
#COLUMN_NAMES: x | y | fval | pA | pB -1.200000e+00 1.000000e+00 6.776000e+00 1.000000e+01 1.000000e+00
_output_rosenbrock_with_keys_.dat: file with "key=value" format without any header:
X = -1.200000e+00 ; Y = 1.000000e+00 ; fval = 6.776000e+00 ; fA = 1.000000e+01 ; fB = 1.000000e+00 ;
Function optimisation is dealt in Uranie with the TOptimizer class. In order to manage both types of evaluation functions
(C++ functions or external codes), two constructors are available.
To build a TOptimizer object from a C++ function, use the following constructor:
TOptimizer(TDataServer *tds, void (*fcn)(double*,double*), TString sinput, TString soutput)
TOptimizer(TDataServer *tds, const char *fcn, TString sinput="", TString soutput="")
This is used to create a TOptimizer object from the TDataServer object, and an analytic function
either given by a void pointer (first line) or by its name (second line) when it has been
loaded in ROOT's memory. The rest of the arguments are the list of the input attributes found in the TDataServer,
sinput, and the output attribute to be created in the TDataServer, soutput. These two arguments
are now compulsory when using a constructor with a pointer of function (for more details on this, see Section I.2.5).
Note that the parameter sinput can be left empty, and the value "" is then interpreted as
"all the input attributes".
To build a TOptimizer object from an external code, use the following constructor:
TOptimizer( TDataServer *tds, TCode *code)
This is used to create a TOptimizer object from the TDataServer, and the TCode external
code.
Tip
To find information about the creation of a TCode, please refer to the Section IV.3.
The first goal of the optimisation module of Uranie is to find the minimum of a function (C++ function or external
code), defined from 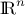 in
in 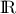 .
.
Two algorithms can be used to seek the minimum of a function: the Migrad or Simplex algorithms, included in the Minuit package of ROOT. Below are excerpts from the Which Minimizer to Use page of Minuit2, ROOT's optimiser library that can be used in Uranie:
In order to select the algorithm to be used, apply the method setMethod to the TOptimizer object, with
argument one of the keywords kMigrad or kSimplex respectively for Migrad or Simplex
algorithm:
TOptimizer * topt = new TOptimizer(tds, myCode);
topt->setMethod(TOptimizer::kSimplex);
// or opt->setMethod(TOptimizer::kMigrad);If not specified, the default algorithm used by the Optimizer module is the Migrad algorithm.
As was previously mentioned, the TOptimizer class is dedicated to the research of the minimum of functions that take
values in 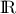 . But it
is also possible to find the minimum of a function that returns multiple values that we want to minimise along one
of these values, by selecting the output value to consider as the one to minimise. To select the return value the
function will be optimised for, use the
. But it
is also possible to find the minimum of a function that returns multiple values that we want to minimise along one
of these values, by selecting the output value to consider as the one to minimise. To select the return value the
function will be optimised for, use the selectCost method, with the name of the output among
which the optimisation will be performed as argument:
// definition of the output file
TOutputFileDataServer *fOutputFile = new TOutputFileDataServer("_output_rosenbrock_with_values_rows_.dat");
fOutputFile->addAttribute(new TAttribute("fa"));
fOutputFile->addAttribute(new TAttribute("fb"));
fOutputFile->addAttribute(new TAttribute("fval"));
// definition of the code
TCode *mycode = new TCode(tds,"rosenbrock -r");
mycode->addOutputFile( fOutputFile );
// TOptimizer
TOptimizer * toptC = new TOptimizer(tds, mycode);
toptC->selectCost("fval"); // "fval" is the chosen cost for the optimisationIn order to improve the quality of the optimisation, or to control the time the computation will last, the user can modify a few parameters:
setTolerance(Double_t dtol)sets the tolerance of the optimisation process to
dtol. Default value is 0.01.setMaxIterations(Int_t nmax)sets the maximum number of iterations of the optimisation process to
nmax. Note that theTDataServeris saved after each iteration. Default value is 50.setMaxFunctionCalls(Int_t nmax)sets the maximum number of calls to the function to minimise to
nmax. Default value is 10.000.
Tip
Note that at each iteration, several function calls may be performed.
When dealing with an external code, which is not easily accessible, new possibilities have been introduced to allow to add both input and output variables defined with simple mathematical formulaes. The examples discussed below are taken from the two use-cases, provided in Section XIV.7.2 and Section XIV.7.4 respectively for a function and an external code.
New input variables can be created with the addAttribute method that takes a name and a
formula as arguments.
tds->addAttribute("xshift","x-0.1");
tds->addAttribute("yshift","y+0.2");
Once done, the TOptimizer should be warned to used these variables by:
specifying the list of inputs for a function constructor:
gROOT->LoadMacro("UserFunctions.C"); TOptimizer *toptfunc = new TOptimizer(tds, "rosenbrock", "xshift:yshift","out");setting the way to write these inputs in the input file (instead of the original ones)
tds->getAttribute("xshift")->setFileKey("input_rosenbrock_with_keys.dat","x"); tds->getAttribute("yshift")->setFileKey("input_rosenbrock_with_keys.dat","y");
New output variables are introduced by calling a new method called addOutputVariable whose
only argument is the list of formulaes to be applied separated by semi-colons. In both cases (function and code)
it looks like this:
topt->addOutputVariable("fval+1:fval*fval:fval*3");
Once done, the optimisation can be done on any of these newly defined variable, simply using the
selectCost as
topt->selectCost("fval+1");
Warning
These functionnalities are tested both for code and function optimisation, but we do not recommend to use it in
the latter case. These computations are indeed requesting TTree operations which are
slow with respect to the execution's time of an analytic function. In this case we strongly recommend to modified
the function at hand to get the expected variables.
The second goal of the optimisation module of Uranie is to find the optimal set of parameters of a model which minimises the distance between reference values and estimation from the model.
Two distances are implemented:
The root mean square deviation:
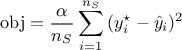
where:
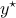 is the
reference values vector;
is the
reference values vector;
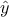 is the estimated
values vector;
is the estimated
values vector;
 is a weight
coefficient for the objective.
is a weight
coefficient for the objective.
This distance is used with the following
TOptimizermethod:addObjective(TString name, TDataServer *tds, TString ystar, TOutputFile *outfile, TString yhat, Double_t weight)The parameters are:
name: the name of the objective to add;
tds: the
TDataServerthat contains the reference values;ystar: the name of the output attribute in the
TDataServertds;outfile: the
TOutputFilewhere the output values of the code are stored;yhat: the name of the output attribute in the output file;
weight (optional): a coefficient to multiply the result by. The default value, if not specified, is 1.
the weighted root mean square deviation:
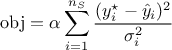
where:
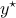 is the
reference values vector;
is the
reference values vector;
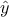 is the estimated
values vector;
is the estimated
values vector;
 is a weight
coefficients vector for the different values;
is a weight
coefficients vector for the different values;
 is a weight
coefficient for the objective.
is a weight
coefficient for the objective.
This distance is used with the following
TOptimizermethod:addObjective(TString name, TDataServer *tds, TString ystar, TString sigma, TOutputFile *outfile, TString yhat, Double_t weight)The parameters are:
name: the name of the objective to add;
tds: the
TDataServerthat contains the reference values;ystar: the name of the output attribute in the
TDataServertds;sigma: the name of the weight attribute in the
TDataServertds (used only in the second method);outfile: the
TOutputFilewhere the output values of the code are stored;yhat: the name of the output attribute in the output file;
weight (optional): a coefficient to multiply the result by; the default value if not specified is 1.
The objectives previously defined can be set active or inactive thanks to the methods
activeObjective(TString name) and unactiveObjective(TString name),
which both take the name of the objective as a parameter.
In order to easily invert the state of all the objectives defined, use the invertObjective()
method. By default, all the objectives added are actives.
In order to consider attributes as fixed parameters, they can be set fixed or unfixed thanks to the methods
fixParameter(TString name) and unfixParameter(TString name), which
both take the name of the objective as a parameter.
In order to easily invert the state of all the parameters defined, use the
invertParameters() method. By default all the parameters are unfixed.
Once the optimisation object is constructed and associated with costs/objectives, the optimisation is simply
performed by calling the optimize() method. The call to this method fills the dataserver specified in
the constructor with the best solution found by the optimisation algorithm.