Documentation / User's manual in C++ :

In order to obtain a modular system, three abstraction levels are distinguished:

Ideally, the combination of any classes of this three levels are possible. In real world, some combinations are useless (do not distribute a sequential algorithm) or impossible (many algorithm cannot converge if an non-calculable evaluation occurs).

As you can see from the defined layers, the architecture is designed to realise many evaluations in parallel. It deals both with a parallel evaluation and with a parallel studies (island optimisation for example). A feasibility test have been done with a parallel evaluation, but it needs extra works from the user.

Now let's start with a first hello world program. It treats the classical Rosenbrock optimisation problem (already introduced in Section VII.2.1). The script below starts with namespace directive, continues with the user supplied evaluation function, and ends with the study procedure. This procedure follows a bottom-up definition: used variables, evaluation function declaration, used resources, and study. Variables are used to define the evaluation prototype and the study (item definition variables, etc), and link these definitions together. In this example, some declarations may seem redundant, but they show their relevance in a more complicated example.

using namespace URANIE::DataServer;
using namespace URANIE::Relauncher;
using namespace URANIE::Reoptimizer;

void rosenbrock(double *in, double *out)
{
    double x, y, d1, d2;
    x = in[0]; y = in[1];
    d1 = (1-x);
    d2 = (y-x*x);
    out[0] = d1*d1 + d2*d2;
}

void Rosenbrock()
{
    // problem variables 
    TAttribute x("x", -3.0, 3.0),
               y("y", -4., 6.),
               ros("rose");

    // user evaluation function
    TCIntEval eval(rosenbrock);
    eval.addInput(&x);
    eval.addInput(&y);
    eval.addOutput(&ros);

    // resources
    TSequentialRun run(&eval);
    run.startSlave();
    if (run.onMaster()) {
        // data server
        TDataServer tds("rosopt", "Rosenbrock Optimisation");
        tds.addAttribute(&x);
        tds.addAttribute(&y);

        // optimisation
        TVizirGenetic algo;
        TVizir2 study(&tds, &run, &algo);
        study.addObjective(&ros);
        study.solverLoop();

        // save results
        tds.exportData("rosenbrock.dat");

        run.stopSlave();
    }
}

This example will not be detailed, it is showed for its structure that you may find again on other studies. however, it must be self explanatory.

An important aspect needs to be pointed out. It concerns the resource handling. This script deals with both the study side and the evaluation side which may be treated by different resources. Both sides need to know variables and evaluation function, while study objects are only useful on study side. Here is the frame of the code that deals with it.

void Study()
{
// both side definitions
...

run.startSlave(); // slave is evaluation side
if (run.onMaster()) { // master is study side
// study definitions
...

run.stopSlave();
}
}

A translation of this code may be: once one starts the study, evaluation-needed objects are defined and evaluation-resources could start their loop waiting for items. The study-resource are allocated from the onMaster method and many things are done from there: distributing the evaluations and collecting the results. Once the study is finished (or at least, no more evaluation is needed), evaluation-resources can be stopped: they stop their loop, exit and jump the study instruction bloc which is no concern to them.

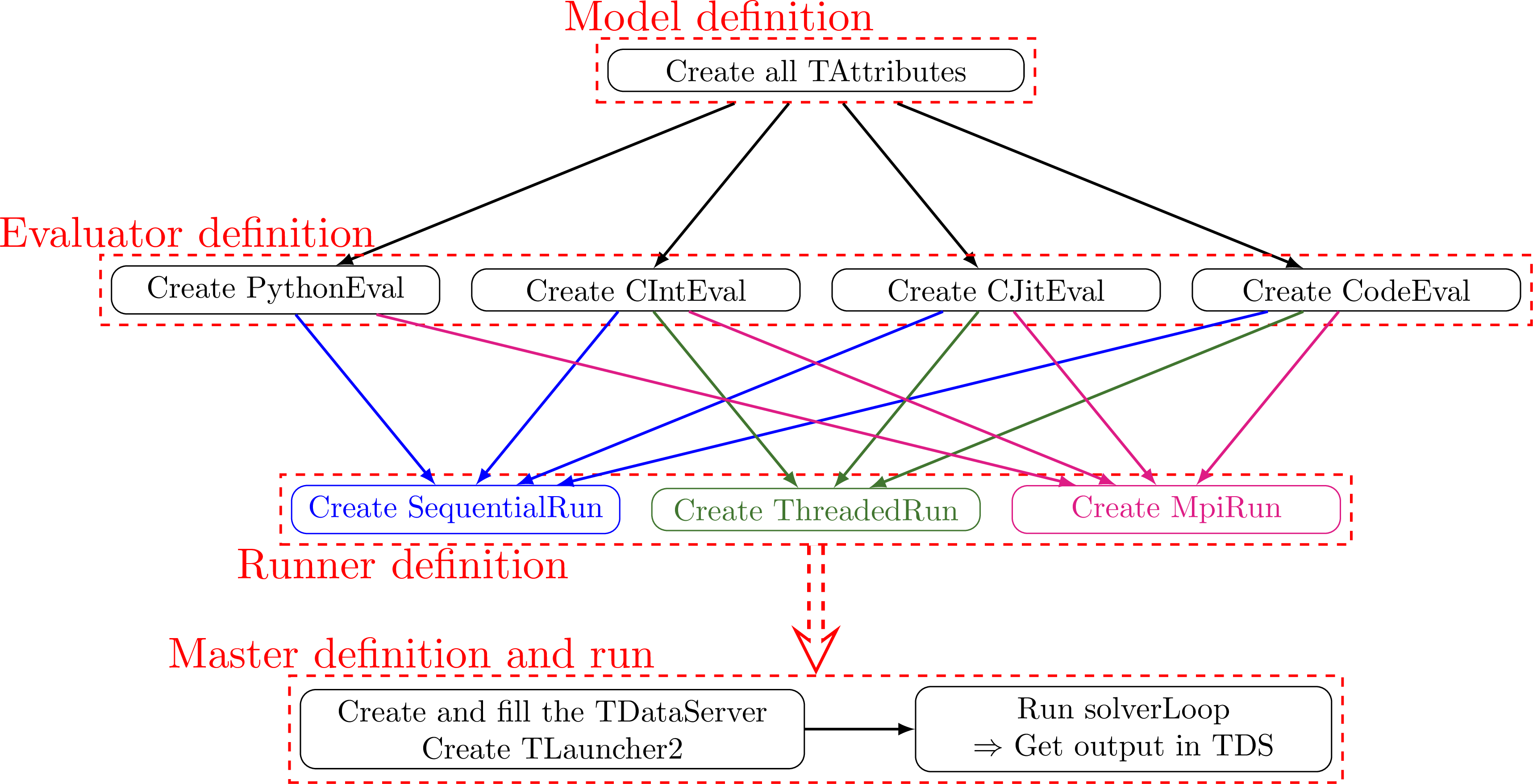
Finally the use of Relauncher module can be sketched in a four-steps process starting as usual, by defining the problem/model to be tested, defining the rule to be applied on the various inputs (meaning configuring the assessors also knowing the way one wants to run these calculations), choosing the corresponding runner and launch the computation through the TLauncher2 instantiation (or any other TMaster inheriting class, such as the ones defined in the Reoptimizer module for optimisation problem, see Chapter IX). The colored arrows in Figure VIII.1 show the allowed associations of assessors and runners (to respect, for instance, the thread-safe properties of the assessors).

Figure VIII.1. Schematic description of the needed steps to define a relauncher procedure

The next three sections will successively pass through the different level of abstraction, starting from the bottom level to the top one.