Documentation
/ Manuel utilisateur en C++
: 
Local solvers proposed by Uranie come from the NLopt library (Non Linear OPTimization). This library is developed by Steven G. Johnson, integrating many original algorithms in an uniform interface. The NLopt website provides many useful information, that enhance the succinct ones provided here. The example used as support for this part is given in Section XIV.9.1 with a specification with respect to the way it was described in Section IX.2.2: since there is no multicriteria solver implemented from NLopt, the criteria on the distortion is downgraded to a constraint using a randomly defined threshold (set to 14).
The TMaster subclass for local optimizer is called TNlopt.
Local optimization starts from an initial guess point. This point has to be defined using the
setStartingPoint method with an integer to precise the dimension, as first argument and a
double * as second argument. This has changed in order to be complient with python but also
to be able to check that the provided number of double is matching the dimension of our problem under
consideration. You can call the setStartingPoint method many times. In C++, it could look like
this:
TNlopt opt(&tds, &runner, &solv);
...
vector<double> p{0.2,0.3};
opt.setStartingPoint(p.size(),&p[0]);
In this case, each optimization, starting from a corresponding starting point, may be done in parallel using
an appropriate TRun. If the results of the optimisation is not consistent when changing the
starting points, this might be a sign for a problem with local minimum. In this case a safer (but slower) solution
might be to consider using global solvers.
To modify the default configuration, the setMaximumEval method, with an
int as only argument, may be used. The default value is 10 000. For multi starting point, it
is interpreted as the accumulation of all evaluations.
Uranie proposes different Nlopt solvers. For direct solvers, there is:
TNloptCobyla: Constrained Optimization BY Linear Approximation from M.J.D.Powell works. The only direct algorithm that supports constraints naturally.TNloptBobyqa: Bounded Optimization BY Quadratic Approximation from M.J.D.Powell works. It is usually quicker than the previous one, but might give nonphysical results if the problem should not be assumed to be quadratic.TNloptPraxis: It uses the PRincipal AXIS method of Richard Brend. This algorithm has a stochastic part.TNloptNelderMead: The well known Nelder-Mead Simplex algorithm.TNloptSubplexe: a simplex variant, the Tom Rowan's subplex algorithm.
and for gradient-based solvers:
TNloptMMA: Method of Moving Asymptotes from Krister Svanberg works. It deals with nonlinear inequality constraints naturally.TNloptSLSQP: Sequential Least-Squares Quadratic Programming from Dieter Kraft. It deals with both inequality and equality constraints naturally.TNloptLBFGS: an implementation of the Limited memory Broyden-Fletcher-Goldfarb-Shanno algorithm written by Ladislaw lukan.TNloptNewtown: A preconditioned inexact truncated Newtown algorithm written by Ladislaw Lukan.TNloptVariableMetric: An implementation of shifted limited-memory variable-metric by Ladislaw lukan.
You may notice that actually none of Nlopt global solvers is provided.
Tip
Remarks for the gradient case: oftenly one does not have access to the real gradient. In this case a finite
difference method is used by doing 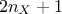 computation around every point, which implies:
computation around every point, which implies:
a code that will provide results with a sufficient accuracy so that the gradient is not always assumed to be null (which can happen when a code returns a value with a very low number of digits). Even with a non-null estimation, the gradient accuracy needs to be sufficient since gradient-based solver usually estimates the Hessian matrix.
a possible parallelisation of the computation.






