Documentation / User's manual in C++ :

XI.2. Calibration classes, distance functions, observations and model

XI.2. Calibration classes, distance functions, observations and model
	Chapter XI. The Calibration module

XI.2. Calibration classes, distance functions, observations and model

This section introduces the common part of all analysis in the Calibration module. Indeed the methods discussed hereafter will be using the same architecture and will be needing a common list of items listed here:

the model have to be settled as this is what one wants to calibrate. It can comes either as a Relauncher::TRun instance, as a Launcher::TCode or a Launcher's function. This part is introduced in Section XI.2.1 (for the general concept and the difference with the usual organisation of model definition) and discussed later-on (mainly for the TCalibration-inheriting object constructor) in Section XI.2.3 and in the dedicated section in each method.
the reference observations have to be defined once and for all so that the model can be run for every newly define set of parameter's value (every new configuration). This part is discussed first in Section XI.2.1 and the way to provide them is also partly discussed in Section XI.2.2.
a distance function as to be created, usually within the calibration instance, to be able to quantify how close the model under study can mimic a set of reference observations. This part is discussed in Section XI.2.2.
a main object has to be created, a calibration method instance, that inherits from the TCalibration class. This is discussed in Section XI.2.3.

XI.2.1. General introduction on data and model definition

All calibration problem will have, at least, two TDataServer objects:

The reference one, usually called tdsRef, which contains the observations (both input and output attributes) onto which the calibration is about to be performed. It is generally read from a simple input file as done below:
```
TDataServer *tdsRef = new TDataServer("reference","my reference");
tdsRef->fileDataRead("myInputData.dat");
```
the parameter one, usually called tdsPar, it contains only attributes and must be empty of data. Its purpose is to define the parameters that should be tested in the calibration process and, depending on the method chosen, will only contain TAttribute members (for minimisation, see Section XI.3) or only TStochasticAttribute inheriting objects for all other methods. The latter case gathers the method doing the analytical computation when the chosen priors are allowed (see Section XI.4) along with all those that require generating one or more design-of-experiments (see Section XI.5 but also Section XI.6).

This step, which should represent the first lines of the calibration procedure, goes along with the model definition. This one is tricky with respect to all the examples provided in Section XIV.4 and in Section XIV.8 as the inputs of the model are coming from two different TDataServers, they can be split into to two categories:

the reference ones will only have values from the reference input file myInputData.dat, meaning that for every configuration, a reference attribute will take the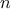 predefined values.
the parameter ones whose value will be changed every time a new configuration will be tested: this value is constant for all the entry of the reference datasets.

Depending on the way the model is coded (and more likely on the parameters the user would like to calibrate) these attributes might not be separated in term of orders, meaning that the list of inputs of a model might look a bit like this:

// Example of input list for a fictive model (whatever the launching solution is chosen)
// ref_var1, ref_var2, ref_var3, ref_var4 are coming from the tdsRef dataserver
// par1, par2 are coming from the tdsPar dataserver 
TString sinputList="ref_var1:par_1:ref_var2:ref_var3:ref_var4:par_2";

Warning

As a result, there is no implicit declaration allowed in the calibration classes constructor and a particular attention must be taken when defining the model: the user must provide the list of inputs (for Launcher-type model) or fill the input and output list into the TEval-inheriting object in the correct order (for Relauncher-type model). This is further discussed in Section XI.2.3.

Finally, all model considered for calibration should have exactly as many outputs (whatever their name are) than the number of output to be compared with (the output attributes in the tdsRef TDataServer object). These outputs are those that will be used to compute the chosen agreement (meaning the result of the distance function) which is the only quantifiable measurement we have between the reference and the predictions for a given configuration). At the end of a calibration process, the user can found three different kinds of information (more can be added if needed, see Section XI.2.3.4)

the resulting parameter's value (or values depending on the chosen method, as some of them are providing several configurations) are being stored in the parameter TDataServer object: as this object was provided empty and should contain only an attribute per parameter to be calibrated, it seems to be the best place to store results. This is obviously the expected target but it should not be considered conclusive without having a look at the two other ones
the agreement between the reference data and the model predictions, which are stored in the parameter TDataServer object tdsPar for every kept configuration;
the residues: the difference between the model predictions and the reference data for every 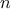, using the a priori and a posteriori configuration. These are stored in a dedicated TDataServer object, called the EvaluationTDS (referred to as tdsEval) and it is mainly called through the drawResidues method (discussed in Section XI.2.3.7). If one wants to access it, it is possible to get a hand on it by calling the getEvaluationTDS() method. The residues are important to check that the behaviour our the newly performed calibration does not show unexpected and unexplained tendency with respect to any variables in the defined uncertainty setup, see the dedicated discussion on this in [metho]

XI.2.2. Defining data and distance functions

The different distance function already embedded in Uranie can be found in Section XI.1.1 and are further discussed, from a theoretical point of view in [metho]. From the user point of view, on the other hand, every distance function is inheriting from the class TDistanceFunction, as can be seen in Figure XI.1, which is purely virtual (meaning that no object can be created as an instance of TDistanceFunction) and which deals with several main purposes:

it loads the reference data once and store them in internally as a vector of vector (or as a vector of TMatrixD depending on the chosen formalism used to compute the distance itself);
once done, the following loop will be called as long as one needs to test new configuration (by configuration we call a new set of values for the 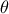vector):
1. it runs the chosen model (disregarding the nature of the object: TRun, TCode...) on the full reference datasets to get the new predictions.
2. it loads the new model predictions for the configuration under study into a vector of vector (or as a vector of TMatrixD depending on the chosen formalism).
3. it computes the distance using both vectors as stated by the equations in Section XI.1.1. This computation is done within the localeval method (which is the only method that should be redefined if a user wants to create its own distance function, see dedicated discussion in Section XI.2.2.2).

On a technical point of view, the TDistanceFunction inherits from the TDoubleEval class which is a part of the Relauncher module. This inheritance is not very important as its main appeal is to considerably simplify the implementation of the minimisation methods with the Reoptimizer module, allowing to simply use all TNlopt algorithms but also the Vizir solutions (see Section XI.3).

Disregarding the considered calibration method, a distance function must be used to compare data and model predictions. This is true even for the TLinearBayesian class which only computes the analytical posterior distribution as the residues are computed both a priori and a posteriori in order to see the improvement of the prediction and possibly their consistency within the uncertainty model (see discussion in [metho]). In most of the case (if not all) the object will be constructed with the recommended way (discussed in Section XI.2.2.1). Another possibility is anyway discussed in Section XI.2.2.2

Whatever the situation (either discussed in Section XI.2.2.1 or in Section XI.2.2.2), once a calibration instance is created (for the sake of genericity we will use here an instance, named cal, of the fake class TCalClass as if it were inheriting from the TCalibration class), the first method to be called is the setDistanceAndReference, as this is the method with which one defines both the type of distance function and the observation ensemble. The former is further discussed in this section and the latter is crucial as without observations no calibration can be done.

XI.2.2.1. Recommended distance function construction method

The recommended way to create a distance function is to call a method implemented in the TCalibration class, which is inherited in every calibration method classes. This method, is called setDistanceAndReference and the prototype we're discussing here is the following:

void setDistanceAndReference(const char *funcName, TDataServer *tdsRef, const char *input, const char *reference, const char *weight="");

It takes up to five elements which are:

funcname: the name of the distance function describes of the already implemented one, as discussed in Section XI.1.1. The possibility are
- "L1" for TL1DistanceFunction
- "LS" for TLSDistanceFunction
- "RelativeLS" for TRelativeLSDistanceFunction
- "WeightedLS" for TWeightedLSDistanceFunction
- "Mahalanobis" for TMahalanobisDistanceFunction
tdsRef: the TDataServer in which the observations are stored;
input: the input variables stored in the TDataServer tdsRef which have been defined as inputs in the code just before creating the calibration object. This argument has the usual attribute list format "x:y:z".
reference: the reference variables stored in the TDataServer tdsRef, with which the output of the code or function will be compared to. This argument has the usual attribute list format "out1:out2:out3".
weight: this argument is optional and can be used to define the name of the (single) variable stored in the TDataServer tdsRef which should be used, in the case of a TWeightedLSDistanceFunction, to fill the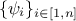 , i.e. the weights used to ponderate each and every observations with respect to the others (see Section XI.1.1).
Warning
A word of cautious about the string to be passed: the number of variable in the list weight should match the number of output of your code that you are using to calibrate your parameters. Even in the peculiar case where you'll be doing calibration with two outputs, one being free of weights, then one should add a "one" attribute to provide for the peculiar output if the other one needs uncertainty model.

Once this method is called, the distance function is created and is stored within the calibration object. It might be needed to put a hand on it for some option, but this is further discussed in Section XI.2.2.3.

The following line summarise this construction in a case where an instance cal of the fake class TCalClass (as if this class were inheriting from the TCalibration class) is created.

// Define the dataservers
TDataServer *tdsRef = new TDataServer("reference","myReferenceData");
// Load the data, both inputs (ref_var1 and ref_var2) and a single output (ref_out1).
tdsRef->fileDataRead("myInputData.dat");
...
TDataServer *tdsPar = new TDataServer("parameters","myParameters");
tdsPar->addAttribute( new TNormalDistribution("par1",0,1) );
// the parameter to calibrate
...
// Define the model
...
// Create the instance of TCalClass:
TCalClass *cal = new TCalClass(); // Constructor is discussed later-on
// Define the Least-Square distance
cal->setDistanceAndReference("LS", tdsRef, "ref_var1:ref_var2", "ref_out1");

In this fake example, the distance function is the Least-square one, and it will used the 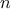values of both inputs "ref_var1" and "ref_var1" and output "ref_out1" stored in tdsRef to calibrate the parameter "par1". No observation weight is needed in this case, as least-square does not require it and as there is only a single output, no variable weight has to be defined as well.

XI.2.2.2. Creating its own distance function

It is possible, if one wants to use a distance function not already implemented in Uranie to ???

XI.2.2.3. Options usable for every distance function

All distance function classes inherit from the TDistanceFunction one and the only difference between all of them is the implementation of the localeval function. This means that a very large fraction of the code is shared by all the distance function object, including the part that deals with their configurations and options.

This part is gathering all the share options that can be configured either through the optional "Option" in several method and constructors, or by accessing the distance function object itself once created. In order to do so, one should call the getDistanceFunction method that will return (if it has been created) the distance function instance stored in the calibration instance under consideration. The following lines provide an example in the case where one is dealing with and instance cal, of the fake class TCalClass (as if it were inheriting from the TCalibration class)

// Creating the calibration instance from a TDataServer and a Relauncher::TRun           
TCalClass *cal = new TCalClass(tdsPar,runner,1,"");
// Creating the distance function (a least square one)
cal->setDistanceAndReference("LS",tdsRef,"logRe:logPr","logNu");
// Retrieving the instance to be able to change options
TLSDistanceFunction *dFunc = (TLSDistanceFunction*)cal->getDistanceFunction();

In the last line of the previous code bloc, the right hand side of the equality started by a cast of the pointer that is returned by getDistanceFunction. As this method returns a pointer to a TDistanceFunction, in C++ one should precise that here, this object is indeed an instance of TLSDistanceFunction.. In the case of python, this is not needed and the equivalent code bloc should look like this:

XI.2.2.3.1. Define the variable weights

In the case where there are several variables used to compare predictions and observations, one might want to ponderate their contribution to the distance. To do two methods are available, both called setVarWeights. Their difference is only the prototype :

// Prototype 1
void setVarWeights( int nwei, double *wei );
// Prototype 2
void setVarWeights( vector<double> wei);

The idea behind this two prototypes is to have a way to control the number of elements in the array of double, either by asking the user to provide it (in prototype 1) or as a by-product of the vector structure. From there, if the size of the array is matching the number of output variables the weights are initialised, the program will crash otherwise.

XI.2.2.3.2. Dump all the estimations

Whatever the construction and evaluation-type (either based on Launcher or Relauncher), you might want to keep track of all evaluations and not only the global distance for all the reference observations. This is possible by calling the TDistanceFunction's method:

void dumpAllDataservers();

This methods takes no argument and sets a boolean to true (by default it is set to false) which implies that every configurations will be dumped as an ASCII file that would be named following this convention: Calibration_testnumber_XX.dat where XX is the configuration number for the under-study analysis.

Warning

Two words of caution:

this options might dump a very large number of files which can fill your local disk (if you're testing functions for instance for which the limit on the number of configuration is not really a limit).
used with a runner architecture (Relauncher-type evaluator), the parameters are not kept by default in the dataserver (they're defined as ConstantAttribute). To get the required behaviour (meaning having parameter's value in the ASCI file), the user should also call a TDistanceFunction's method called
```
void keepParametersValue();
```
This function, which takes no argument, just set to true the final argument of all TLauncher2's call of addConstantAttribute.

XI.2.2.3.3. Define the observations covariance matrix

In the case where the observations are correlated with a known covariance structure, this covariance can be precised as a TMatrixD using the following method:

void setObservationCovarianceMatrix(TMatrixD &mat);

This method and the possibility to define a covariance structure between the observations is only relevant when the distance function is an instance of the TMahalanobisDistanceFunction.

XI.2.2.3.4. Specify a Launcher object or options

This method is very specific as it can be used for all calibration classes, but only if the model introduced is a Launcher::TCode. This option pops up here, because the distance function is the place where the model is used to estimate the new predictions for a newly set parameter vector (see Section XI.2.2). This option allows not to use the usual TLauncher object in order to use one of the other instance. This is done in a single function:

void changeLauncher(TString tlcName);

The only argument of this method is a TString object which is used to used of the two other instance in the Launcher module for the TCode: either the TLauncherByStep or the TLauncherByStepRemote. When used, the setDrawProgressBar method is also called to set this variable to false.

The main point of this is to switch from an usual TLauncher object to another one chosen by the user. Among the possible solutions one can set

TLauncherByStep: if the user wants to breakdown the launching process, decomposing the into preTreatment, run and postTreatment.
TLauncherByStepRemote: if the user wants to use the code on a cluster on which Uranie is not installed. This is not recommended for any cluster set-up as all the CEA clusters are. This is based on the libssh library, see Section IV.4.5 for more details.

Finally, the default option for the run method of whatever kind of TLauncher-inheriting instance is noIntermediateSteps, that prevents the safety writing of the results into a file every five estimations. Two methods can be applied on a TDistanceFunction objects to change these options:

// Adding more options to the code launcher run method
void addCodeLauncherOpt(TString opt);
// Change the code launcher run method options
void changeCodeLauncherOpt(TString opt);

The first one is written to keep the default and add more options on top, for instance options that would allow to distribute the computation with the fork process (as a reminder, this option is "localhost=X" where X stands for the number of threads to be used). On the other hand, the second method above allow to restart from scratch in order to define the options has chosen by the user.

XI.2.2.3.5. Dump the distance details

In the case where one do not understand or trust the way the distance are computed, it is possible to dump the details of their computation (warning this is really verbose). This can be done by calling the dumpDetails, whose prototype is pretty simple:

void dumpDetails();

XI.2.3. The calibration classes common methods

All the calibration classes that derive from TCalibration share a lot of common methods and their organisation has been factorised as much as possible. This section will describe all this shared code, preventing repetition in the upcoming sections that will deal with every specific calibration method (from Section XI.3 to Section XI.6).

From Section XI.2.3.1 to Section XI.2.3.3, one discusses the different constructor explaining the different way the model could be provided and what it implies while Section XI.2.3.4 provides a glimpse of the shared possible options that can be defined and their purpose. Finally Section XI.2.3.6 and Section XI.2.3.7 introduce the drawing method in their principle (but illustration for them will be postponed to the dedicated method in the rest of this documentation).

Warning

As for some of the discussions above, the following methods are common to all TCalibration-inheriting classes, so the example provided will be written using an instance cal of the fake class TCalClass (as if this class were inheriting from the TCalibration class). A more realistic syntax should be found in the dedicated sections (from Section XI.3 to Section XI.6).

The calibration classes can, generally, be constructed with 4 different ways, linked to the way the model has been precised. To estimate how close the new set of parameter values (the configuration) is to the reference data, one needs to be able to run the model on the data's input variable. The input variables of the observation datasets are not the only input variable of the model used within the calibration method, as the parameters themselves have to be specified as inputs (as they also obviously affect the predictions). This section shows, in the fictive case of a not existing TCalClass class how to construct our calibration objects.

XI.2.3.1. Construction with a runner

This constructor is using the Relauncher architecture. This approach allows a simple way to change the evaluator (to pass from a C++ function to a python's one or a code) but also to use either a sequential approach (for a code) to a threaded one (to distribute locally the estimations). This approach is partly discussed in Chapter VIII.

The constructor in this case, should look like this

// Constructor with a runner
TCalClass(TDataServer *tds, TRun *runner, Int_t ns=1, Option_t *option="")

It takes up to four elements which are:

tds: a TDataServer object containing only an attribute for every parameter to be calibrated. This is the TDataServer object called tdsPar, defined in Section XI.2.1.
runner: a TRun-inheriting instance that contains all the model information and whose type is defining the way to distribute the estimation: it can either be a TSequentialRun instance or TThreadedRun for distributed computations.
ns: the number of samples to be produced. This field only applies to methods for which more than one configuration are expected which is not the case for local minimisation with a single point initialisation but also for linear Bayesian analysis (see Section XI.4). The default value is 1.
option: the option that can be applied to the method. The option common to all calibration classes (so those defined in the TCalibration class) are discussed in Section XI.2.3.4.

The key step in this constructor is the TRun-inheriting instance creation. As already stated, its type is giving the lead on the way to distribute the estimations. When one is constructing such an object, it is done by passing an evaluator, whose list is already largely discussed in Section VIII.3.

Taking back the formalism already introduced in Section XI.2.2.1, the model instance of a function Foo, a classical TCIntEval function, is created as done below, when this model takes the following inputs ref_var1, par1 and ref_var2 and it produce a single output to be compared with "ref_out1" (the comparison between this reference and the model prediction is done through the distance function, as already discussed Section XI.2.2.1 in for this example).

// Define the dataservers
TDataServer *tdsRef = new TDataServer("reference","myReferenceData");
// Load the data, both inputs (ref_var1 and ref_var2) and a single output (ref_out1).
tdsRef->fileDataRead("myInputData.dat");
...
TDataServer *tdsPar = new TDataServer("parameters","myParameters");
tdsPar->addAttribute( new TNormalDistribution("par1",0,1) ); // the parameter to calibrate
...

// Define the model if a function Foo(double *x, double *y)  is defined above
// for which x[0]=ref_var1, x[1]=par1 and x[2]=ref_var2 and y[0] is the model prediction
TCIntEval *model = new TCIntEval("Foo");
// Add inputs in the correct order
model->addInput(tdsRef->getAttribute("ref_var1"));
model->addInput(tdsPar->getAttribute("par1"));
model->addInput(tdsRef->getAttribute("ref_var2"));
// Define the output attribute
TAttribute *out = new TAttribute("out");
model->addOutput(out);
// Define a sequential runner to be used
TSequentialRun *runner = new TSequentialRun(model);    

...
// Create the instance of TCalClass:
int ns=1;
TCalClass *cal = new TCalClass(tdsPar, runner, ns, "");

XI.2.3.2. Construction with a `TCode`

This constructor is using the Launcher architecture. This approach is pretty different from the Relauncher one, as it is only focusing on the code case.

The constructor in this case, should look like this

// Constructor with a TCode
TCalClass(TDataServer *tds, TCode *code, Int_t ns=1, Option_t *option="")

It takes up to four elements which are:

tds: a TDataServer object containing only an attribute for every parameter to be calibrated. This is the TDataServer object called tdsPar, defined in Section XI.2.1.
code: a TCode instance containing the output file (or files) that list the output attributes while all input attributes have been assigned an input file by the usual methods (setFileKey, setFileFlag...).
ns: the number of samples to be produced. This field only applies to methods for which more than one configuration are expected which is not the case for local minimisation with a single point initialisation but also for linear Bayesian analysis (see Section XI.4). The default value is 1.
option: the option that can be applied to the method. The option common to all calibration classes (so those defined in the TCalibration class) are discussed in Section XI.2.3.4.

Unlike the runner constructor discussed above, this construction does not bring any information on the way the computation will be performed. The run method is called for every configuration with the following options as a default: noIntermediateSteps, that prevents the safety writing of the results into a file every five estimations and quiet that prevents the launcher to be too verbose. Two methods can be applied on a TDistanceFunction objects to change these options:

// Adding more options to the code launcher
void addCodeLauncherOpt(TString opt);
// Change the code launcher option 
void changeCodeLauncherOpt(TString opt);

Taking back the formalism already introduced in Section XI.2.2.1, the model instance of a code Foo, using a TCode instance, is shown below, when this model takes the following inputs ref_var1, par1 and ref_var2 and it produces a single output to be compared with "ref_out1" (the comparison between this reference and the model prediction is done through the distance function, as already discussed Section XI.2.2.1 in for this example).

// Define the dataservers
TDataServer *tdsRef = new TDataServer("reference","myReferenceData");
// Load the data, both inputs (ref_var1 and ref_var2) and a single output (ref_out1).
tdsRef->fileDataRead("myInputData.dat");
...
TDataServer *tdsPar = new TDataServer("parameters","myParameters");
tdsPar->addAttribute( new TNormalDistribution("par1",0,1) ); // the parameter to calibrate
...

TString sIn = TString("code_foo_input.in");
// Set the reference input file and the key for each input attributes
tdsRef->getAttribute("ref_var1")->setFileKey(sIn, "var1");
tdsRef->getAttribute("ref_var2")->setFileKey(sIn, "var2");
tdsPar->getAttribute("par1")->setFileKey(sIn, "par1");
// The output file of the code
TOutputFileRow *fout = new TOutputFileRow("_output_code_foo_.dat");
// The attribute in the output file
fout->addAttribute(new TAttribute("out"));
// Creation of the code
TCode *code = new TCode(tdsRef, "foo -s -k");
mycode->addOutputFile( fout );

...
// Create the instance of TCalClass:
int ns=1;
TCalClass *cal = new TCalClass(tdsPar, code, ns, "");

XI.2.3.3. Construction for a function with the Launcher architecture

This constructor is using the Launcher architecture and deals with a function (C++ one with the usual prototype).

The constructors in this case, should look like this

// Constructor with a function pointer using Launcher
TCalClass(TDataServer *tds, void (*fcn)(Double_t*,Double_t*), const char *varexpinput, const char *varexpoutput, int ns=1, Option_t *option="");
// Constructor with a function name using Launcher            
TCalClass(TDataServer *tds, const char *fcn, const char *varexpinput, const char *varexpoutput, int ns=1, Option_t *option="");

It takes up to six elements, four of which are compulsory:

tds: a TDataServer object containing only an attribute for every parameter to be calibrated. This is the TDataServer object called tdsPar, defined in Section XI.2.1.
fcn: the second argument is either the name of the function or a pointer to this function. A good knowledge of this function implies that the user must know in which order the input and output variables are provided.
varexinput: the list of input variables in the correct order, as an admixture of the reference attributes and the parameter attributes.
varexpoutput: the list of output variables.
ns: the number of samples to be produced. This field only applies to methods for which more than one configuration are expected which is not the case for local minimisation with a single point initialisation but also for linear Bayesian analysis (see Section XI.4). The default value is 1.
option: the option that can be applied to the method. The option common to all calibration classes (so those defined in the TCalibration class) are discussed in Section XI.2.3.4.

This constructor is the simplest one, as all information are provided on a single line, no option has to be defined and no file should be created. Taking back the formalism already introduced in Section XI.2.2.1, the model being considered is the function Foo, and the construction using the pointer prototype is shown below, when this model takes the following inputs ref_var1, par1 and ref_var2 and it produces a single output to be compared with "ref_out1" (the comparison between this reference and the model prediction is done through the distance function, as already discussed Section XI.2.2.1 in for this example).

// Define the dataservers
TDataServer *tdsRef = new TDataServer("reference","myReferenceData");
// Load the data, both inputs (ref_var1 and ref_var2) and a single output (ref_out1).
tdsRef->fileDataRead("myInputData.dat");
...
TDataServer *tdsPar = new TDataServer("parameters","myParameters");
tdsPar->addAttribute( new TNormalDistribution("par1",0,1) ); // the parameter to calibrate
...

// Create the instance of TCalClass:
int ns=1;
TCalClass *cal = new TCalClass(tdsPar, Foo, "ref_var1:par1:ref_var2", "out", ns, "");

XI.2.3.4. Running the estimation

Once the calibration-object is constructed and its distance function is also created, the aim is to perform the calibration, meaning that the best value (or values) of the parameters have to be estimated. This is done by calling the method

void estimateParameters(Option_t *option="");

This method is global and it mainly call another internal method, defined in every TCalibration-inheriting class, in which the real estimation is performed.

There are different options that can be applied to the estimateParameters method, among which:

"saveAllEval": this option allows to keep every single estimations in the internal dataserver that is later-on used to produce residue plots (see Section XI.2.3.7). WARNING: this can very likely become unbearable, as the number of estimation to keep might be gigantic.
"noAgreement": this options allows to get rid of the agreement attribute at the end of the estimation if one considers the information is pointless.

Also, some options, not discussed here because they're triggered by calling methods on the TDistanceFunction-inheriting instance, might be of use to understand and validate the way the calibration has been performed. For this, see Section XI.2.2.3.

There are few methods used to represent the results. The skeleton are defined within the TCalibration class (even though some might not applied to few specific method). This section introduces the general concept and every calibration method particularity will be discussed within the proper method section.

XI.2.3.5. Estimate custom residues

Once the estimation is performed, the a priori and a posteriori residuals are estimated, meaning that from both set of parameter values (the a priori and a posteriori values estimation will depend on the chosen algorithm so this is not specified here) one can ask to re-evaluate the residuals once another set of parameter values is provided. This can be done through

void estimateCustomResidues(string resName, int theta_nb, double *theta_val);

which takes three arguments:

resName: the name of the set to be kept as a tag;
theta_nb: the number of values provided in the array (must be coherent with _nPar obviously);
theta_val: the value of the parameters to be used as an array.

This construction should be called simply with a vector<double>numpy array for the sake of simplicity as shown below.

vector<double> mypar = {0., 2., 3.};
mycal->estimateCustomResidues("set1", mypar.size(), &mypar[0]);

The idea behind all this is to be able to re-estimate residuals when the a posteriori values of the parameter might have to be carefully estimated provided the sample available in after the estimation (for instance in the case of Markov-Chain to get rid of the warming-up estimations). Once done, the selection can be used in the drawResidues function discussed later-on in Section XI.2.3.7.

XI.2.3.6. Drawing the parameters

This method's purpose is to draw parameter's value. The prototype is the following

void drawParameters(TString sTitre, const char *variable = "*", const char *select = "1>0", Option_t * option = "");

It takes up to four arguments, three of which are optional:

sTitre

The title of the plot to be produced (an empty string can be put).

variable

This field should contain the parameter list to be drawn (with the usual format of parameter's name splitted by ":"). The default value is to draw all parameters (the "*" field).

select

A selection field to remove some kept configurations (for instance if you want to consider the burn-in period or lag procedure for the Metropolis-Hasting algorithm, see Section XI.6).

option

The optional field can be used to tune a bit the plots, options being separated by commas

"nonewcanvas": if this option is used the plot will be done in an existing canvas, if not, a new TCanvas will be created on the spot.
"vertical": if this option is used and more than one parameters have to be displayed, the canvas is splitted into as many windows as parameters in the variable list, the windows being stacked one above the others, using the full width. The default is "horizontal" so the plots are side-by-side.

XI.2.3.7. Drawing the residues

This method's purpose is to draw output variable's residue, meaning the difference between the model predictions and the reference output. Two kinds of residues are generally discussed: the a priori ones (from the initialisation values of the parameters) and the a posteriori ones (the results of the calibration procedure). The prototype is the following

void drawResidues(TString sTitre, const char *variable = "*", const char *select="1>0", Option_t * option = "");

It takes up to four arguments, three of which are optional:

sTitre

The title of the plot to be produced (an empty string can be put).

variable

This field should contain the output variable list to be drawn (with the usual format of parameter's name splitted by ":"). The default value is to draw all variables (the "*" field).

select

A selection field to remove some of the observations from the reference datasets.

option

The optional field can be used to tune a bit the plots, options being separated by commas

"nonewcanvas": if this option is used the plot will be done in an existing canvas, if not, a new TCanvas will be created on the spot.
"vertical": if this option is used and more than one parameters have to be displayed, the canvas is splitted into as many windows as parameters in the variable list, the windows being stacked one above the others, using the full width. The default is "horizontal" so the plots are side-by-side.
"apriori/aposteriori": these options state whether only the a priori residues (with "apriori") or only the a posteriori (with "aposteriori") field. If none of this two fields is used, both kind of residues should be drawn.
"custom=XXX": this option state whether one also wants to show the custom residues estimate through the esimateCustomResidues method already introduced in Section XI.2.3.5. With the example provided in the aforementionned section, the command can look like this, if one wants to compare a priori, a posteriori and the "set1" custom set:
```
mycal->drawResidues("Residual title", "*", "", "nonewcanvas,apriori,aposteriori,custom=sel1");
```

Summary: TCalibration and TDistanceFunction

In summary, a calibration analysis should always follow these key steps:

Define both the parameter (tdsPar) and reference (tdsRef) objects, as explained in Section XI.2.1.
Define the model architecture (either Relauncher or Launcher-based) and the evaluator kind (code, C++-function, python-function...). A peculiar attention is needed to specify the input and output attributes (the former should be an admixture of attributes from tdsPar and tdsRef, as explained in Section XI.2.1.
Define the TCalibration-inheriting object (meaning the underlying method chosen for this analysis) and construct it (see from Section XI.2.3.1 to Section XI.2.3.3).
Define the TDistanceFunction-inheriting object by calling the TCalibration's method setDistanceAndReference, see the recommended method in Section XI.2.2.1.
Set the method-dependent parameters (discussed in dedicated part, from Section XI.3 to Section XI.6).
Call the estimateParameters method with selected options (see Section XI.2.3.4).
Do the post-treatment thanks to method-dependent functions discussed in dedicated part, from Section XI.3 to Section XI.6) and drawing methods (see also both Section XI.2.3.6 and Section XI.2.3.7).

XI.2.4. Use-case for this chapter

In order to illustrate the ongoing methods in the future sections, a bit more closely than the already introduced dummy examples, a general use-case will be used. This use-case rely on the flowrate model introduced (along with a descriptive sketch) in Chapter IV and whose equation is recalled below:

Equation XI.1. Flowrate function

where the eight parameters are:

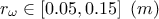: radius of borehole
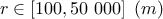: radius of influence
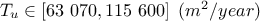: Transmitivity of the superior layer of water
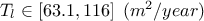: Transmitivity of the inferior layer of water
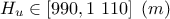: Potentiometric "head" of the superior layer of water
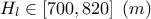: Potentiometric "head" of the inferior layer of water
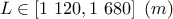: length of borehole
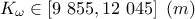: hydraulic conductivity of borehole

This example has been treated by several authors in the dedicated literature, for instance in [worley1987deterministic]. With respect to our concerns, the idea of the upcoming examples (in this chapter, along with those in the use-case macros section, see Section XIV.11) is to consider that one has an observation sample. For this function, we consider that from all the inputs, only two are have been varie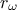d ( and 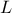) and only one is actually unknown: 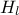. The rest of the variables are set to a frozen value: 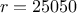, , 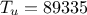, , 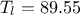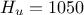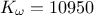. This can be written as the following function (using the usual C++ prototype)

void flowrateModel(double *x, double *y) {
  double rw = x[1], r = 25050;
  double tu = 89335, tl = 89.55;
  double hu = 1050, hl = x[0];
  double l = x[2], kw = 10950;

  double num = 2.0 * TMath::Pi() * tu * (hu - hl);
  double lnronrw = TMath::Log(r / rw);
  double den = lnronrw * (1.0 + (2.0 * l * tu) / (lnronrw * rw * rw * kw) + tu / tl);

  y[0] = num / den;
}

As discussed previously, this function shows that one might be aware of the way the inputs are organised. In this case, the parameter to be calibrated (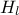) comes first while the varying inputs ( 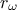and 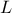) come later. The first lines of all examples should look like this

// Name of the input reference file
TString ExpData="Ex2DoE_n100_sd1.75.dat";

// define the reference
TDataServer *tdsRef = new TDataServer("tdsRef","doe_exp_Re_Pr");
tdsRef->fileDataRead(ExpData.Data());

// define the parameters
TDataServer *tdsPar = new TDataServer("tdsPar","pouet");
tdsPar->addAttribute(new TAttribute("hl",700.0,760.0)); // if stochastic laws are needed
// use tdsPar->addAttribute( new TUniformDistribution("hl", 700.0, 760.0) );

// Create the output attribute
TAttribute *out = new TAttribute("out");


Chapter XI. The Calibration module		XI.3. Using minimisation techniques

Documentation / User's manual in C++ :

XI.2. Calibration classes, distance functions, observations and model

XI.2.1. General introduction on data and model definition

Warning

XI.2.2. Defining data and distance functions

XI.2.2.1. Recommended distance function construction method

Warning

XI.2.2.2. Creating its own distance function

XI.2.2.3. Options usable for every distance function

XI.2.2.3.1. Define the variable weights

XI.2.2.3.2. Dump all the estimations

Warning

XI.2.2.3.3. Define the observations covariance matrix

XI.2.2.3.4. Specify a Launcher object or options

XI.2.2.3.5. Dump the distance details

XI.2.3. The calibration classes common methods

Warning

XI.2.3.1. Construction with a runner

XI.2.3.2. Construction with a TCode

XI.2.3.3. Construction for a function with the Launcher architecture

XI.2.3.4. Running the estimation

XI.2.3.5. Estimate custom residues

XI.2.3.6. Drawing the parameters

XI.2.3.7. Drawing the residues

XI.2.4. Use-case for this chapter

XI.2.3.2. Construction with a `TCode`