Documentation / User's manual in C++ :

XI.5. The Approximation Bayesian Computation techniques (ABC)

XI.5. The Approximation Bayesian Computation techniques (ABC)
	Chapter XI. The Calibration module

XI.5. The Approximation Bayesian Computation techniques (ABC)

This sections is discussing methods gathered below the ABC acronym, which stands for Approximation Bayesian Computation. The idea behind these methods is to perform Bayesian inference without having to explicitly evaluate the model likelihood function, which is why these methods are also referred to as likelihood-free algorithms [wilkinson2013approximate].

As a reminder of what's discussed in further details in [metho], the principle of the Bayesian approach is recap in the equation 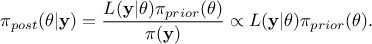where 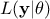represents the conditional probability of the observations knowing the values of 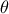, 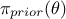is the a priori probability density of 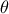(the prior) and 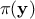is the marginal likelihood of the observations, which is constant (for more details see [metho]).

On the technical point of view, methods in this section will inherit from the TABC class (which itself inherits from the TCalibration one, in order to benefit from all the already introduced features). So far the only ABC method is the Rejection one, discussed in [metho] and whose implementation has been done through the TRejectionABC class discussed below.

The way to use our Rejection ABC class is summarised in few key steps here:

Get the reference data, the model and its parameters. The parameters to be calibrated must be TStochasticAttribute-inheriting instances. Choose the assessor type you'd like to use and construct the TRejectionABC object accordingly with the suitable distance function. Even though this mainly relies on common code, this part is introduced also in Section XI.5.1.
Provide algorithm properties, to define optional behaviour and precise the uncertainty hypotheses you want, through the methods discussed in Section XI.5.2.
Finally the estimation is performed and the results can be extracted or draw with the usual plots. The specificities are discussed in Section XI.5.3.

XI.5.1. Constructing the RejectionABC object

The constructors that can be used to get an instance of the TRejectionABC class are those detailed in Section XI.2.3. As a reminder the prototype available are these ones:

// Constructor with a runner
TRejectionABC(TDataServer *tds, TRun *runner, Int_t ns=1, Option_t *option="");
// Constructor with a TCode
TRejectionABC(TDataServer *tds, TCode *code, Int_t ns=1, Option_t *option="");
// Constructor with a function  using Launcher
TRejectionABC(TDataServer *tds, void (*fcn)(Double_t*,Double_t*), const char *varexpinput, const char *varexpoutput, int ns=1, Option_t *option="");;
TRejectionABC(TDataServer *tds, const char *fcn, const char *varexpinput, const char *varexpoutput, int ns=1, Option_t *option="");

The details about these constructor can be found in Section XI.2.3.1, Section XI.2.3.2 and Section XI.2.3.3 respectively for the TRun, TCode and TLauncherFunction-based constructor. In all cases, the number of samples 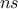has to set and represents the number of configurations kept in the final sample. An important point is discussed below about the algorithm properties, as to know how many computations will be done, as from our implementation, it actually depends on the percentile value chosen, see Section XI.5.2.1.

As for the option, there is a specific option which might be used to change the default value of the a posteriori behaviour. The final sample is a distribution of the parameters value and if one wants to investigate the impact of the a posteriori measurement, two possible choice can be made to get a single-point estimate that would best describes the distribution:

use the mean of the distribution: the default option chosen
use the mode of the distribution: the user needs to add "mode" in the option field of the TRejectionABC constructor.

The default solution is straightforward, while the second needs an internal smoothing of the distribution in order to get the best estimate of the mode.

The final step here it to construct the TDistanceFunction which is the compulsory step which should always come right after the constructor, but a word of caution about this step:

Warning

In the case where you are comparing your reference datasets to a deterministic model (meaning no intrinsic stochastic behaviour is embedded in the code or function) then you might want to specify your uncertainty hypotheses to the method, as discussed below in Section XI.5.2.2.

XI.5.2. Define the TRejectionABC algorithm properties

Once the TRejectionABC instance is created along with its TDistanceFunction, there are few methods that can be of use in order to tune the algorithm parameters. All these methods are optional in the sens that there are default value, each are detailed in the following sub-sections.

XI.5.2.1. Define the percentile

The first method discussed here is rather simple: the idea behind the rejection is to kept the best configuration tested and this can be done either by looking at the distance results themselves with respect to a threshold value (called 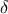in [metho]) or looking at a certain fraction of configurations, defined through a percentile 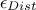. The latter is the one implemented in the TRejectionABC method so fat, the default being 1%, which can be written

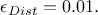
In order to change this, the user might want to call the method

void setPercentile(double eps);

in which the only argument is the value of the percentile that should be kept.

An important consequence of this is that the number of configurations that will be tested is computed as follow

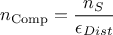
where 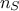is the number of configurations that should be kept at the end.

XI.5.2.2. Introducing noise for deterministic function

As already explained previously, in the case where you are comparing your reference datasets to a deterministic model (meaning no intrinsic stochastic behaviour is embedded in the code or function) then you might want to specify your uncertainty hypotheses to the method. This can be done, by calling the

void setGaussianNoise(const char *stdname);

The idea here to inject random noise (assumed Gaussian and centred on 0) to the model prediction using internal variable in the reference datasets to set the value of the standard deviation. The only argument is a list of variables that should have the usual shape "stdvaria1:stdvaria2" and whose elements represent variable within the reference TDataServer whose values are the standard deviation for every single observation points (which can represents experimental uncertainty for instance). This solutions allows three things:

define a common uncertainty (a general one throughout the observation of the reference datasets) by simply adding an attribute with a TAttributeFormula where the formula would be constant.
use experimental uncertainties are likely to be be provided along the reference values
Store all hypotheses in the reference TDataServer object. For this reason we strongly recommend to save both the parameter and reference datasets at the end of a calibration procedure.

Warning

A word of cautious about the string to be passed: the number of variable in the list stdname should match the number of output of your code that you are using to calibrate your parameters. Even in the peculiar case where you'll be doing calibration with two outputs, one being free of any kind of uncertainty, then one should add a zero attribute to provide for this peculiar output if the other one needs uncertainty model.

XI.5.3. Look at the results

Finally once the computation is done there are two different methods (apart from looking at the final datasets): the two drawing methods drawParameters and drawResidues already introduced respectively in Section XI.2.3.6 and Section XI.2.3.7. There are no specific options or visualisation methods to discuss further.


XI.4. Analytical linear Bayesian estimation		XI.6. The Markov-chain approach