Documentation / User's manual in C++ :

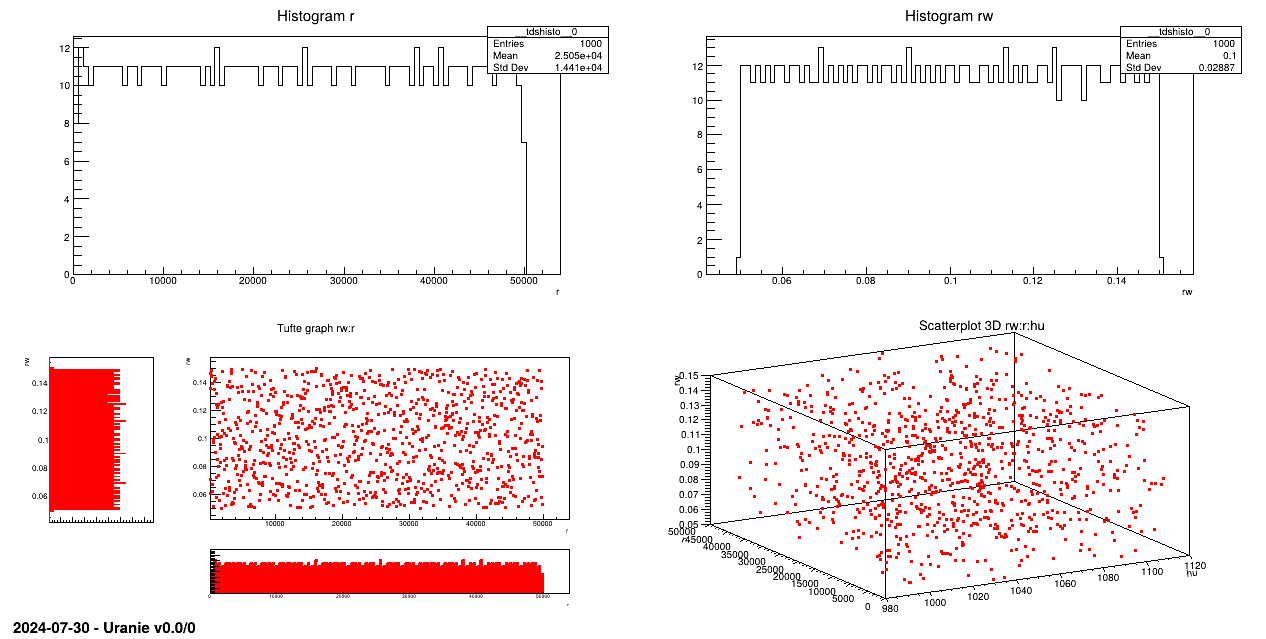
The objective of this macro is to generate a design-of-experiments, of length 100 using the LHS method, with eight random attributes (, , , , 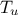, , 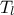, 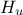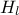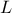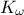) which obey uniform laws on specific intervals.

{
  Int_t nS = 1000;
  // Define the DataServer
  TDataServer *tds = new TDataServer("tdsFlowrate", "Design of experiments for Flowrate");

  // Add the study attributes 
  tds->addAttribute( new TUniformDistribution("rw", 0.05, 0.15));
  tds->addAttribute( new TUniformDistribution("r", 100.0, 50000.0));
  tds->addAttribute( new TUniformDistribution("tu", 63070.0, 115600.0));
  tds->addAttribute( new TUniformDistribution("tl", 63.1, 116.0));
  tds->addAttribute( new TUniformDistribution("hu", 990.0, 1110.0));
  tds->addAttribute( new TUniformDistribution("hl", 700.0, 820.0));
  tds->addAttribute( new TUniformDistribution("l", 1120.0, 1680.0));
  tds->addAttribute( new TUniformDistribution("kw", 9855.0, 12045.0));

    
  // test Generateur de plan d'experience
  TSampling * sampling = new TSampling(tds, "lhs", nS);   
  sampling->generateSample();
  
  tds->exportData("_flowrate_sampler_.dat");

    
  // Visualisation
  TCanvas  *Canvas = new TCanvas("Canvas", "Graph for the Macro samplingFlowrate",5,64,1270,667);
  gStyle->SetPalette(1);
  TPad *pad = new TPad("pad","pad",0, 0.03, 1, 1); pad->Draw();
  
  pad->Divide(2, 2);
  pad->cd(1); tds->draw("r");
  pad->cd(2); tds->draw("rw");
  pad->cd(3); tds->drawTufte("rw:r");
  pad->cd(4); tds->draw("rw:r:hu");

      
}

An uniform law is set for each attribute and then, linked to a the TDataServer:

tds->addAttribute( new TUniformDistribution("rw", 0.05, 0.15));
tds->addAttribute( new TUniformDistribution("r", 100.0, 50000.0));
tds->addAttribute( new TUniformDistribution("tu", 63070.0, 115600.0));
tds->addAttribute( new TUniformDistribution("tl", 63.1, 116.0));
tds->addAttribute( new TUniformDistribution("hu", 990.0, 1110.0));
tds->addAttribute( new TUniformDistribution("hl", 700.0, 820.0));
tds->addAttribute( new TUniformDistribution("l", 1120.0, 1680.0));
tds->addAttribute( new TUniformDistribution("kw", 9855.0, 12045.0));

The sampling is generated with the LHS method:

TSampling * sampling = new TSampling(tds, "lhs", nS);
sampling->generateSample();

Data are exported in an ASCII file:

tds->exportData("_flowrate_sampler_.dat");

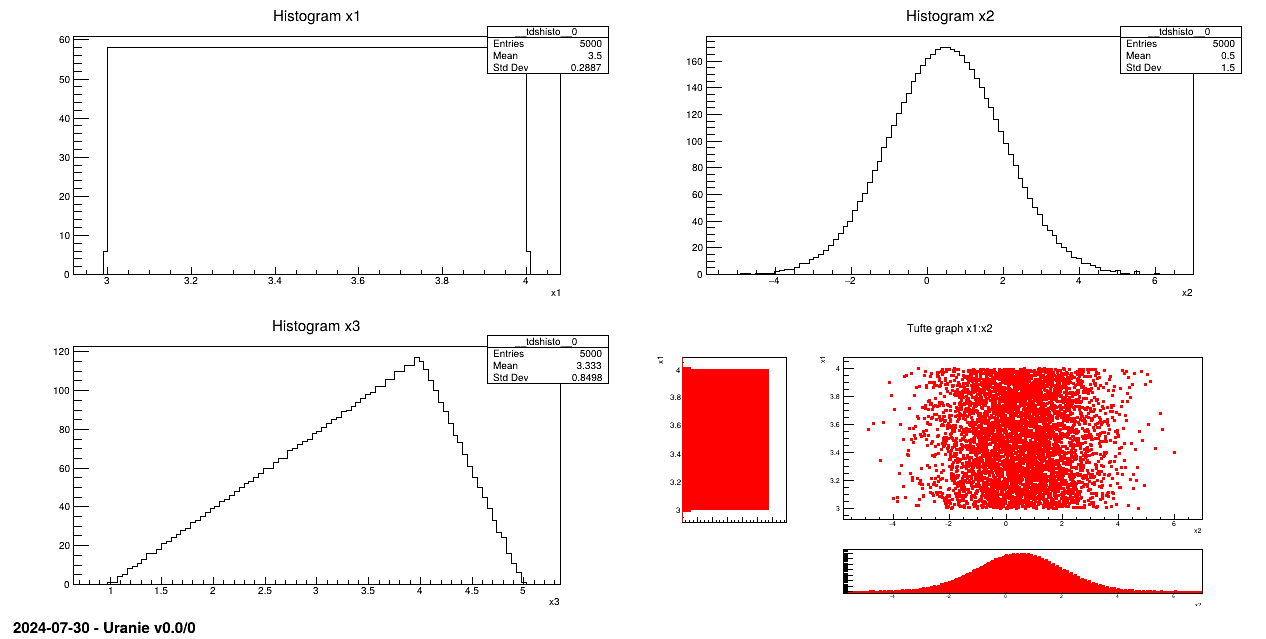
Generate a design-of-experiments of 5000 patterns, using the LHS method, with three random attributes:

 {
  // Create a TDataServer
  TDataServer * tds = new TDataServer();
  // Fill the DataServer with the three attributes of the study
  tds->addAttribute(new TUniformDistribution("x1", 3., 4.));
  tds->addAttribute(new TNormalDistribution("x2", 0.5, 1.5));
  tds->addAttribute(new TTriangularDistribution("x3", 1., 5., 4.));
    
  // Generate the sampling from the TDataServer
  TSampling *sampling = new TSampling(tds, "lhs", 5000);   
  sampling->generateSample();
    
  tds->StartViewer();
  
  // Graph
  TCanvas  *Canvas = new TCanvas("c1", "Graph for the Macro sampling",5,64,1270,667);
  TPad *pad = new TPad("pad","pad",0, 0.03, 1, 1); pad->Draw();
  pad->Divide(2,2);

  pad->cd(1); tds->Draw("x1");
  pad->cd(2); tds->Draw("x2");
  pad->cd(3); tds->Draw("x3");
  pad->cd(4); tds->drawTufte("x1:x2");
        
}

Laws are set for each attribute and linked to a TDataServer:

tds->addAttribute(new TUniformDistribution("x1", 3., 4.));
tds->addAttribute(new TNormalDistribution("x2", 0.5, 1.5));
tds->addAttribute(new TTriangularDistribution("x3", 1., 5., 4.));

The sampling is generated with the LHS method!

TSampling *sampling = new TSampling(tds, "lhs", 5000);
sampling->generateSample();

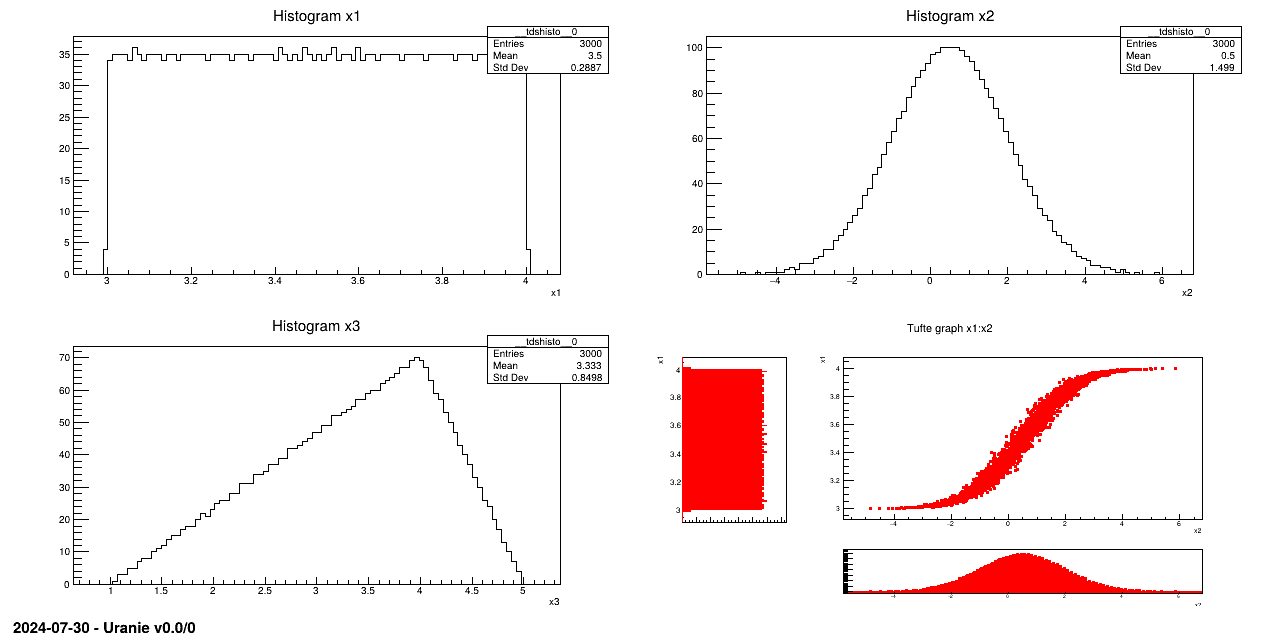
Generate a design-of-experiments, of 3000 patterns using the LHS method, with 3 random attributes and taking into account a correlation between the first two attributes. This correlation, equals to 0.99, is computed using the rank values (the Spearmann definition, c.f. Section III.3 and in [Metho] for more details).

{
  // Create a TDataServer
  TDataServer * tds = new TDataServer();
  // Fill the DataServer with the three attributes of the study
  tds->addAttribute(new TUniformDistribution("x1", 3., 4.));
  tds->addAttribute(new TNormalDistribution("x2", 0.5, 1.5));
  tds->addAttribute(new TTriangularDistribution("x3", 1., 5., 4.));
    
  // Generate the sampling from the TDataServer
  TSampling *sampling = new TSampling(tds, "lhs", 3000);
  sampling->setUserCorrelation(0, 1, 0.99);      
  sampling->generateSample();
    
  tds->exportData("toto.dat","x1:x3");
  tds->exportDataHeader("toto.h","x1:x2");
  
  // Graph
  TCanvas  *Canvas = new TCanvas("c1", "Graph for the Macro samplingCorrelation",5,64,1270,667);
  TPad *pad = new TPad("pad","pad",0, 0.03, 1, 1); pad->Draw();  
  pad->Divide(2,2);

  pad->cd(1); tds->Draw("x1");
  pad->cd(2); tds->Draw("x2");
  pad->cd(3); tds->Draw("x3");
  pad->cd(4); tds->drawTufte("x1:x2");
        
}

Laws are set for each attribute and linked to a TDataServer:

tds->addAttribute(new TUniformDistribution("x1", 3., 4.));
tds->addAttribute(new TNormalDistribution("x2", 0.5, 1.5));
tds->addAttribute(new TTriangularDistribution("x3", 1., 5., 4.));

The sampling is generated with the LHS method and a correlation is set between the two first attributes:

TSampling *sampling = new TSampling(tds, "lhs", 3000);
sampling->setUserCorrelation(0, 1, 0.99);
sampling->generateSample();

Data are partially exported in an ASCII file and a header file:

tds->exportData("toto.dat","x1:x3");
tds->exportDataHeader("toto.h","x1:x2");

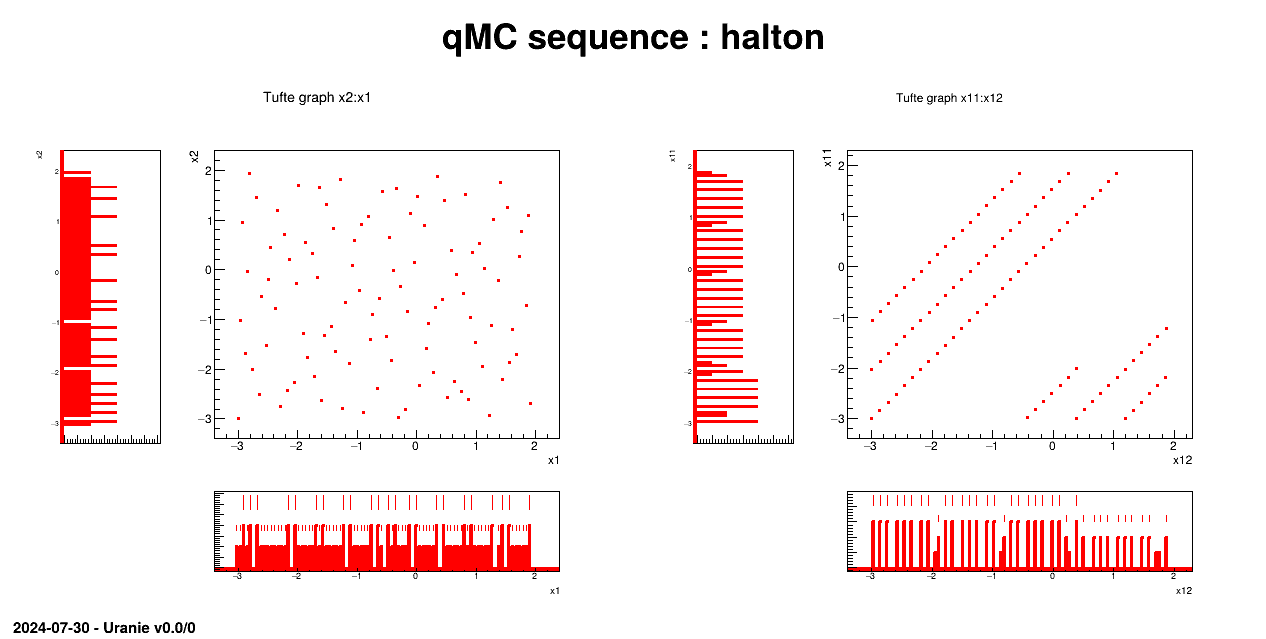
Generate a design-of-experiments of 100 patterns using quasi Monte-Carlo methods ("Halton" or "Sobol") with 12 random attributes, following an uniform law on [3.,2.]. All these information are introduced by variables which will be used by the rest of the macro.

{
  // Parameters
  Int_t nSampler = 100;
  TString sQMC ="halton";     // halton / sobol
  Int_t nVar = 12;
  
  // Create a TDataServer
  TDataServer * tds = new TDataServer();
  
  // Fill the DataServer with the nVar attributes of the study
  for (Int_t ivar=0; ivar<nVar; ivar++)
    tds->addAttribute( new TUniformDistribution(Form("x%d", ivar+1), -3.0, 2.0));
    
  // Generate the quasi Monte-Carlo sequence from the TDataServer
  TQMC * qmc = new TQMC(tds, sQMC, nSampler);
  qmc->generateSample();
    
  // Visualisation
  TCanvas  *Canvas = new TCanvas("c1", "Graph for the Macro qmc",5,64,1270,667);
  Canvas->Range(0,0,25,18);

  TPaveLabel *pl = new TPaveLabel(1,16.3,24,17.5, Form("qMC sequence : %s", sQMC.Data()),"br");
  pl->SetBorderSize(0);
  pl->Draw();

  pad1 = new TPad("pad1", "Determ", 0.02,0.05,0.48,0.88);
  pad2 = new TPad("pad2","Stoch",0.52,0.05,0.98,0.88);
  pad1->Draw();
  pad2->Draw();
  
  pad1->cd(); tds->drawTufte("x2:x1");
  pad2->cd(); tds->drawTufte("x11:x12");
         
}

Laws are set for each attribute and linked to a TDataServer:

for (Int_t ivar=0; ivar<nVar; ivar++)
tds->addAttribute( new TUniformDistribution(Form("x%d", ivar+1), -3.0, 2.0));
	  

The sampling is generated with the QMC method and a correlation is set between the two first attributes:

TString sQMC ="halton";
TQMC * qmc = new TQMC(tds, sQMC, nSampler);
qmc->generateSample();

The rest of the code is used to produce a plot.

The objective is to perform three basic samplings, the first with 10000 variables on 10 patterns using a SRS method, the second with 10000 variables on 10 patterns with a LHS method and the third with 10000 variables on 5000 patterns with a SRS method. Each sampling is related to a specific function, and these three functions are run in a fourth one.

void test_big_sampling(Bool_t bsave = kFALSE)
{
    TDataServer *tds = new TDataServer();
    
    cout << "    - Creating attributes..." << endl;
    for(Int_t i = 0; i < 4000; i++)
        tds->addAttribute(new TUniformDistribution(Form("x_%d",i), 0.0, 1.0));
    
    TBasicSampling *s = new TBasicSampling(tds, "srs", 5000);
    
    cout << "    - Starting sampling..." << endl;  
    s->generateSample();

    if ( bsave ) {
      // WARNING: The generated file is quite big (~300 Mo)    
      cout << "    - Saving data..." << endl; 
      tds->exportData("_sampling_basic_sampling_big_sampling_.dat");
    } else {
      cout << "    - No saving data (bsave = kFALSE); and the generated file is quite big (~300 Mo)." << endl; 
    }
}

void test_small_srs_sampling(Bool_t bsave = kFALSE)
{
    TDataServer *tds = new TDataServer();
    
    cout << "    - Creating attributes..." << endl;
    for(Int_t i = 0; i < 10000; i++)
        tds->addAttribute(new TUniformDistribution(Form("x_%d",i), 0.0, 1.0));
    
    TBasicSampling *s = new TBasicSampling(tds, "srs", 10);
    
    cout << "    - Starting sampling..." << endl;  
    s->generateSample();
    
    if ( bsave ) {
      cout << "    - Saving data..." << endl; 
      tds->exportData("_sampling_basic_sampling_small_srs_sampling_.dat");
    } else
      cout << "    - No saving data (bsave = kFALSE)." << endl; 

}

void test_small_lhs_sampling(Bool_t bsave = kFALSE)
{
    TDataServer *tds = new TDataServer();
    
    cout << "    - Creating attributes..." << endl;
    for(Int_t i = 0; i < 10000; i++)
        tds->addAttribute(new TUniformDistribution(Form("x_%d",i), 0.0, 1.0));
    
    TBasicSampling *s = new TBasicSampling(tds, "lhs", 10);
    
    cout << "    - Starting sampling..." << endl;  
    s->generateSample();
    
    if ( bsave ) {
      cout << "    - Saving data..." << endl; 
      tds->exportData("_sampling_basic_sampling_small_lhs_sampling_.dat");
    } else
      cout << "    - No saving data (bsave = kFALSE)." << endl; 

}

void samplingBasicSampling()
{
  cout << endl << "***************************************************" << endl;
  cout << " ** Test small SRS sampling (10000 attributes, 10 data)" << endl;
  test_small_srs_sampling(kTRUE);
  cout << "***************************************************" << endl;
  gROOT->ls();
 
    
 
  cout << endl << "***************************************************" << endl;
  cout << " ** Test small LHS sampling (10000 attributes, 10 data)" << endl;
  test_small_lhs_sampling(kTRUE);
  cout << "***************************************************" << endl;
  gROOT->ls();
 
    
   
  cout << endl << "***************************************************" << endl;
  cout << " ** Test big sampling (4000 attributes, 5000 data)" << endl;
  test_big_sampling();
  cout << "***************************************************" << endl;
  gROOT->ls();
 
    
}

This part shows the complete code used to produce the console display in Section III.6.3.3.

{
   // step 1
   TDataServer *tds = new TDataServer("tdsoat","Data server for simple OAT design");
   tds->addAttribute(new TAttribute("x1"));
   tds->addAttribute(new TAttribute("x2"));
        
   // step 2
   tds->getAttribute("x1")->setDefaultValue(0.0);
   tds->getAttribute("x2")->setDefaultValue(10.0);
        
   // step 3
   TOATDesign *oatSampler = new TOATDesign(tds, "regular", 4);
        
   // step 4
   Bool_t use_percentage = kTRUE;
   oatSampler->setRange("x1", 2.0);
   oatSampler->setRange("x2", 40.0, use_percentage);
        
   // step 5
   oatSampler->generateSample();
    
   // display
   tds->scan();  
  }

This part shows the complete code used to produce the console display in Section III.6.3.4.

{
   // step 1
   TDataServer *tds = new TDataServer("tdsoat","Data server for simple OAT design");
   tds->addAttribute(new TUniformDistribution("x1", -5.0, 5.0));
   tds->addAttribute(new TNormalDistribution("x2", 11.0, 1.0));   
        
   // step 2
   tds->getAttribute("x1")->setDefaultValue(0.0);
   tds->getAttribute("x2")->setDefaultValue(10.0);
        
   // step 3
   TOATDesign *oatSampler = new TOATDesign(tds, "lhs", 1000);
        
   // step 4
   Bool_t use_percentage = kTRUE;
   oatSampler->setRange("x1", 2.0);
   oatSampler->setRange("x2", 40.0, use_percentage);
        
   // step 5
   oatSampler->generateSample();
    
   TCanvas c("can","can",10,32,1200,600);
   TPad *apad = new TPad("apad","apad",0, 0.03, 1, 1);
   apad->Draw();   
   apad->Divide(2,1);
   apad->cd(1);
   tds->draw("x1","__modified_att__ == 1");
   apad->cd(2);
   tds->draw("x2","__modified_att__ == 2"); 
  }

This part shows the complete code used to produce the console display in Section III.6.3.5.

{
   // step 1
   TDataServer *tds = new TDataServer("tdsoat","Data server for simple OAT design");
   tds->fileDataRead("myNominalValues.dat");      
        
   // step 3
   TOATDesign *oatSampler = new TOATDesign(tds);
        
   // step 4
   Bool_t use_percentage = kTRUE;
   oatSampler->setRange("x1", 2.0);
   oatSampler->setRange("x2", 40.0, use_percentage);
        
   // step 5
   oatSampler->generateSample();
    
   // display
   tds->scan();  
  }

This part shows the complete code used to produce the console display in Section III.6.3.6.

{
   // step 1
   TDataServer *tds = new TDataServer("tds","Data server for simple OAT design");
   tds->fileDataRead("myNominalValues.dat");      
        
   // step 3
   TOATDesign *oatSampler = new TOATDesign(tds);
        
   // step 4
   Bool_t use_percentage = kTRUE;
   oatSampler->setRange("x1", "rx1");
   oatSampler->setRange("x2", 40.0, use_percentage);
        
   // step 5
   oatSampler->generateSample();
    
   // display
   tds->scan();  
  }

This macro shows the usage of the TSpaceFilling class and the resulting design-of-experiments in three simple dataserver cases:

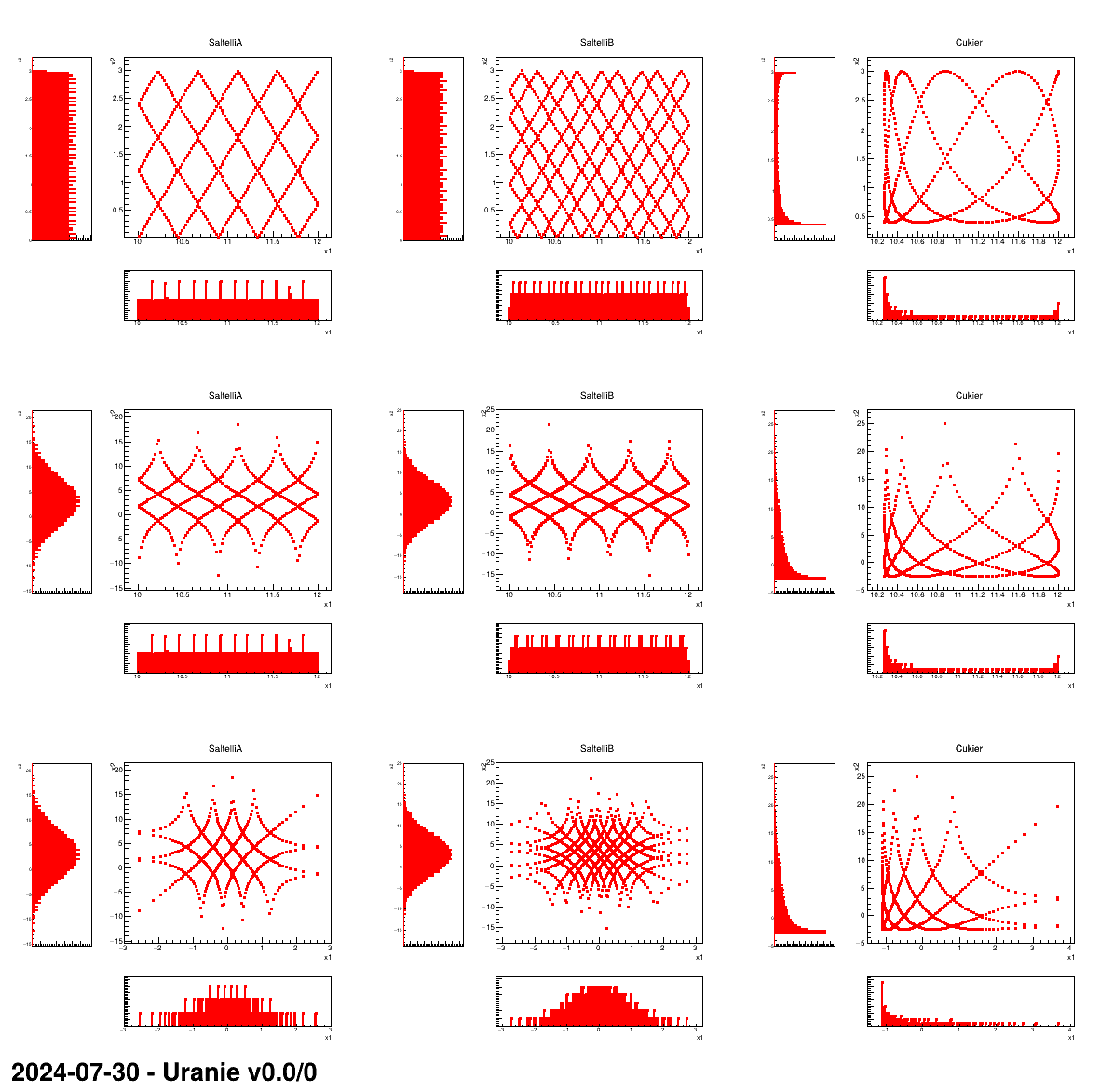
For each of these configurations (represented in the following plot by a line), the three available algorithms are also tested. They are called:

This kind of design-of-experiments is not intented to be used regurlarly, it is requested only by few mechanisms like the FAST and RBD methods which rely on fourier transformations. This macro and, above all, the following plot, is made mainly for illustration purpose.

 
void GenerateAndDrawIt(TPad* pad, TDataServer *tds, TSpaceFilling *tsp, int nb, const char *title)
{
    pad->cd(nb+1);
    tds->deleteTuple();
    tsp->generateSample();
    tds->drawTufte("x2:x1");
    ((TPaveLabel*)(pad->GetPad(nb+1)->GetPrimitive("TPave")))->SetLabel("");
    ((TH1F*)gPad->GetPrimitive("htemp"))->SetTitle(title);
    gPad->Modified();
}

void samplingSpaceFilling()
{
    //Attributes
    TUniformDistribution *att1 =  new TUniformDistribution("x1",10,12);
    TUniformDistribution *att2 =  new TUniformDistribution("x2",0,3);
    TNormalDistribution *nor1 =  new TNormalDistribution("x1",0,1);
    TNormalDistribution *nor2 =  new TNormalDistribution("x2",3,5);

    // Pointer to DataServer and Samplers
    TDataServer *tds[3];
    TSpaceFilling *tsp[9];
    string algoname[3]={"SaltelliA","SaltelliB","Cukier"};
    
    // Canvas to produce the 3x3 plot
    TCanvas *Can = new TCanvas("Can","Can",10,32,1200,1200); 
    TPad *pad = new TPad("pad","pad",0, 0.03, 1, 1); pad->Draw();
    pad->Divide(3,3);
    int counter=0;

    for(unsigned int itds=0; itds<3; itds++)
    {
	// Create a DataServer to store new configuration (UnivsUni, GausvsUni, Gaus vs Gaus)
	tds[itds] = new TDataServer("test","test");
	switch(itds)
	{
	case 0: tds[itds]->addAttribute(att1);  tds[itds]->addAttribute(att2); break;	    
	case 1: tds[itds]->addAttribute(att1);  tds[itds]->addAttribute(nor2); break;
	case 2: tds[itds]->addAttribute(nor1);  tds[itds]->addAttribute(nor2); break;
	}

	// Looping over the 3 spacefilling algo available
	for(unsigned int ialg=0; ialg<3; ialg++)
	{
	    // Instantiate the sampler
	    switch(ialg)
	    {
	    case 0: tsp[counter] = new TSpaceFilling(tds[itds], "srs", 1000, TSpaceFilling::kSaltelliA); break;
	    case 1: tsp[counter] = new TSpaceFilling(tds[itds], "srs", 1000, TSpaceFilling::kSaltelliB); break;
	    case 2: tsp[counter] = new TSpaceFilling(tds[itds], "srs", 1000, TSpaceFilling::kCukier);  break;
	    }
	    //Draw with correct legend
	    GenerateAndDrawIt(pad, tds[itds], tsp[counter], counter, algoname[ialg].c_str());
            counter++;
	}
    }}

This macro shows the usage of the TMaxiMinLHS class in the case where it is used with an already provided LHS grid. The class itself can generate a LHS grid from scratch (on which the simulated annealing algorithm will be applied to get a maximin grid) but the idea for this macro is to do this procedure in two steps to be able to compare the original LHS grid and the results of the optimisation. The orginal design-of-experiments is done with two uniformly-distributed variables.

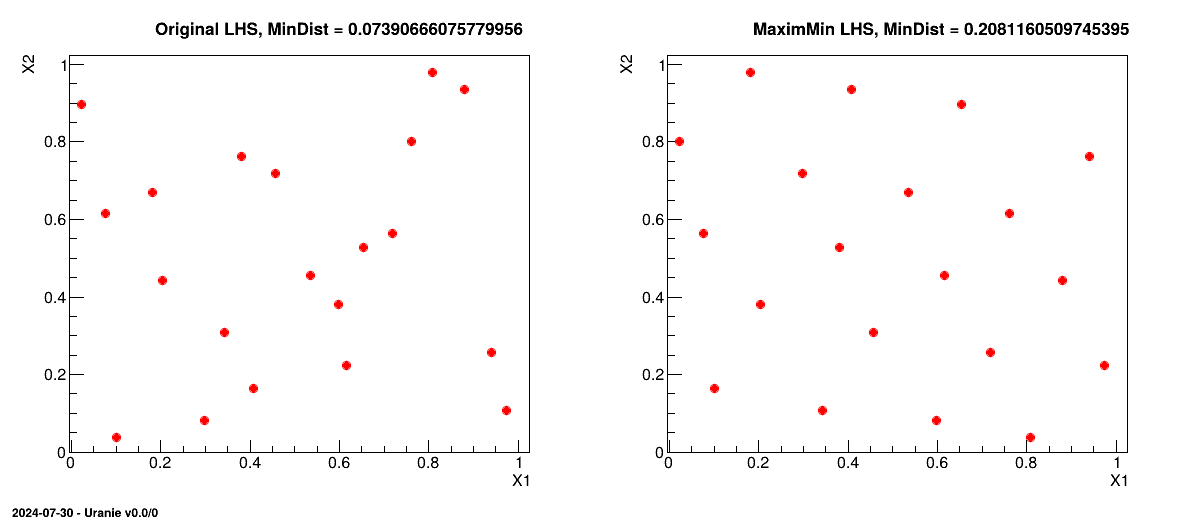
The resulting design-of-experiments presented is presented side-by-side with the original one and the mindist criterion calculated is displayed on top of both grid, for illustration purpose.

void niceplot(TDataServer *tds, TLatex *lat, string Title)
{

    tds->getTuple()->SetMarkerStyle(20); tds->getTuple()->SetMarkerSize(1);
    tds->Draw("X2:X1");
    stringstream sstr; sstr.str("");
    sstr<<Title<<", MinDist="<<TMaxiMinLHS::getMinDist(tds->getMatrix());
    ((TH2F*)gPad->GetPrimitive("__tdshisto__0"))->SetTitle( "" );
    ((TH2F*)gPad->GetPrimitive("__tdshisto__0"))->GetXaxis()->SetRangeUser(0.,1.);
    ((TH2F*)gPad->GetPrimitive("__tdshisto__0"))->GetYaxis()->SetRangeUser(0.,1.);
    lat->DrawLatex(0.25,0.94,sstr.str().c_str());

}

void samplingMaxiMinLHSFromLHSGrid()
{

    // Canvas to produce the 2x1 plot to compare LHS designs
    TCanvas *Can = new TCanvas("Can","Can",10,32,1200,550); 
    TPad *pad = new TPad("pad","pad",0, 0.03, 1, 1);
    pad->Draw();
    pad->Divide(2,1);
    
    int size = 20; // Size of the samples to be produced
    TLatex *lat = new TLatex(); lat->SetNDC(); lat->SetTextSize(0.038); // To write titles

    // Create dataserver and define the attributes
    TDataServer *tds = new TDataServer("tds","pouet");
    tds->addAttribute( new TUniformDistribution("X1",0,1) ); tds->getAttribute("X1")->delShare(); // Define attribute and state to tds that it owns it
    tds->addAttribute( new TUniformDistribution("X2",0,1) ); tds->getAttribute("X2")->delShare(); // Define attribute and state to tds that it owns it

    // Generate the original LHS grid
    TSampling *sampl = new TSampling(tds,"lhs",size);  
    sampl->generateSample();

    // Display it
    pad->cd(1);
    niceplot(tds, lat, "Original LHS");

    // Transform the grid in a maximin LHD
    // Set initial temperature to 0.1, c factor to 0.99 and loop limitations to 300 following official recommandation in methodology manual
    TMaxiMinLHS *maxim = new TMaxiMinLHS(tds, size, 0.1, 0.99, 300, 300);  
    maxim->generateSample();

    // Display it
    pad->cd(2);
    niceplot(tds, lat, "MaximMin LHS");

    
  }

The macro very much looks like any other design-of-experiments generating macro above: the dataserver is created and the problem is defined along with the input variables. A LHS grid is generated through the use of TSampling and display in the first part of the canvas, calling a generic function niceplot defined on top of this macro. The new part comes with the following lines:

// Transform the grid in a maximin LHD
// Set initial temperature to 0.1, c factor to 0.99 and loop limitations to 300 following official recommandation in methodology manual
TMaxiMinLHS *maxim = new TMaxiMinLHS(tds, size, 0.1, 0.99, 300, 300);  
maxim->generateSample();            

The construction line of a TMaxiMinLHS is a bit different from the usual TSampling object: on top of a pointer to the dataserver, it requires the size of the grid to be generated and the main characteristic of the simulated annealing method to be used for the optimisation of the mindist criteria. A more complete discussion is done on this subject in [metho]

This macro shows the usage of the TConstrLHS class when one wants to create a constrained LHS with three linear constraints. In order to illustate the concept, it is applied on three input variables drawn from uniform distribution with well-thought boundaries (as the concept of the LHS is to have nicely distributed marginals).

#include "ConstrFunctions.C"

void nicegrid(TDataServer *tds, TCanvas *Can)
{
    int ns=tds->getNPatterns(), nx=tds->getNAttributes();
    tds->drawPairs();
    TH1F *h[nx];
    TAttribute *att=NULL;
    gStyle->SetOptStat(0);
    for(int iatt=0; iatt<nx; iatt++)
    {
        Can->GetPad(iatt*(nx+1)+1)->cd();
        att=tds->getAttribute(iatt);
        h[iatt] = new TH1F(Form("%s_histo",att->GetName()), Form("%s_histo;x_%i",att->GetName(), iatt), ns, att->getLowerBound(), att->getUpperBound());
        tds->Draw(Form("%s>>%s_histo", att->GetName(), att->GetName()),"","goff");
        h[iatt]->Draw();
    }
}

int samplingConstrLHSLinear()
{
    // Canvas to produce the 2x1 plot to compare LHS designs
    TCanvas *Can = new TCanvas("Can","Can", 10, 32, 1000, 1000);
    
    int ns = 250, nx = 3; // Size of the samples to be produced
    // Create dataserver and define the attributes
    TDataServer *tds = new TDataServer("tds","pouet");
    for(int iatt=0; iatt<nx; iatt++)
    {        
        tds->addAttribute( new TUniformDistribution(Form("x_%i",iatt),0,iatt+1) );
        tds->getAttribute(Form("x_%i",iatt))->delShare(); 
    }
    
    // Generate the constr lhs
    TConstrLHS *constrlhs = new TConstrLHS(tds, ns);
    vector<int> inputs = {1,0,2,1};
    constrlhs->addConstraint(Linear, 2, inputs.size(), &inputs[0]);
    constrlhs->generateSample();

    // Do the plot 
    nicegrid(tds, Can);
  
    return 0;
}

The very beginning of these macros is the nicegrid method which is here only to show the nice marginal distributions and the scatter plots. One can clearly skip this part to focus on the rest in the main function.

The macro very much looks like any other design-of-experiments generating macro above: the dataserver is created along with the canvas object and the problem is defined along with the input variables and the number of locations to be produced. Once done, then the TConstrLHS instance is created with the four following lines:

// Generate the constr lhs
TConstrLHS *constrlhs = new TConstrLHS(tds, ns);
vector<int> inputs = {1,0,2,1};
constrlhs->addConstraint(Linear, 2, inputs.size(), &inputs[0]);
constrlhs->generateSample();          
          

The constructor is pretty obvious, as it takes only the dataserver object and the number of locations. Once created the main method to be called is the addConstraint function which has been largely discussed in Section III.2.4. The first argument of this method is the pointer to the C++ function which has been included in our macro through the very first line:

#include "ConstrFunctions.C"

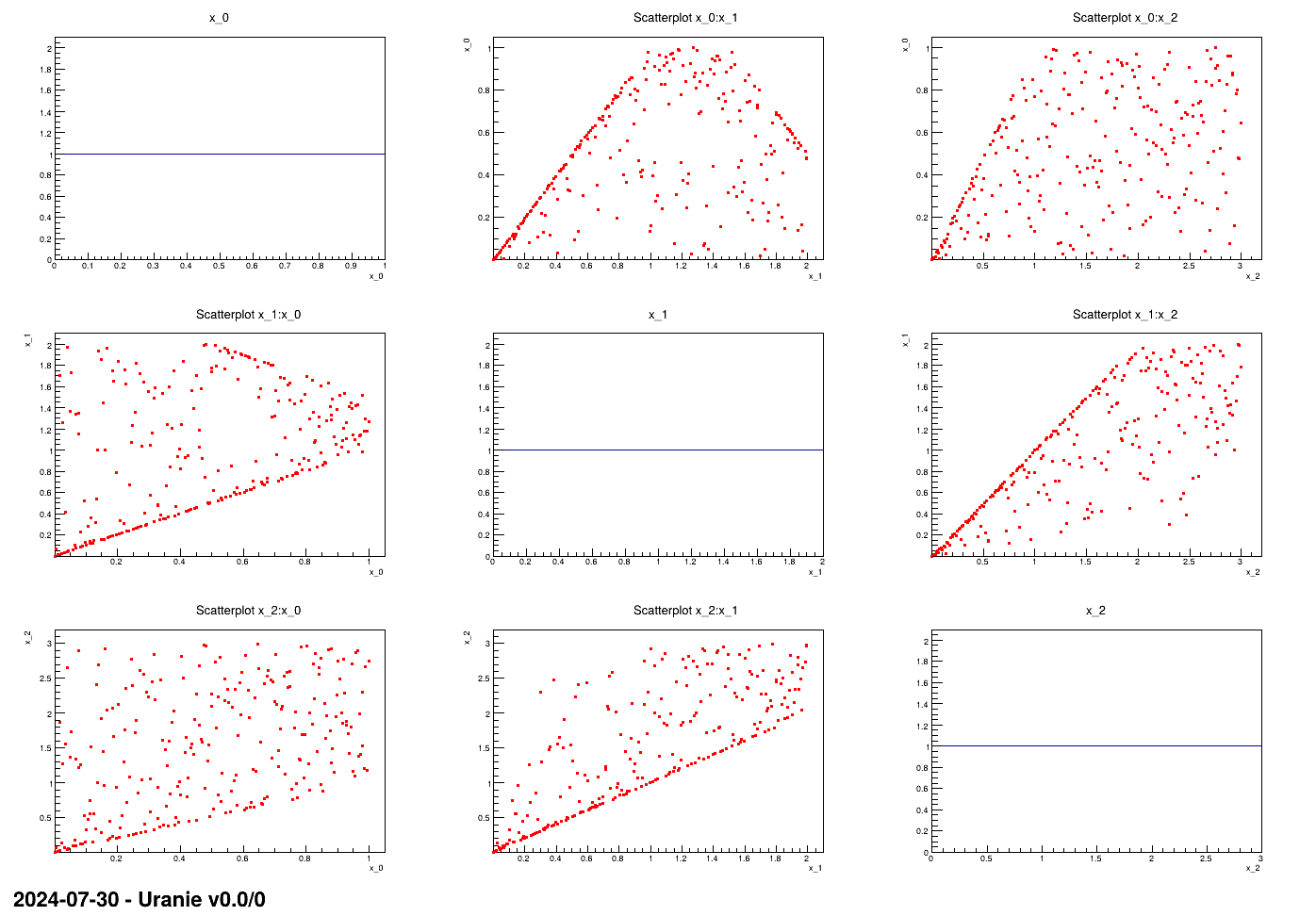
which contains the Linear function. The rest of the argument are the number of constraints, the size of the list of parameters and its content. Finally the nicegrid method is called to produce the nice plot shown in Figure XIV.14

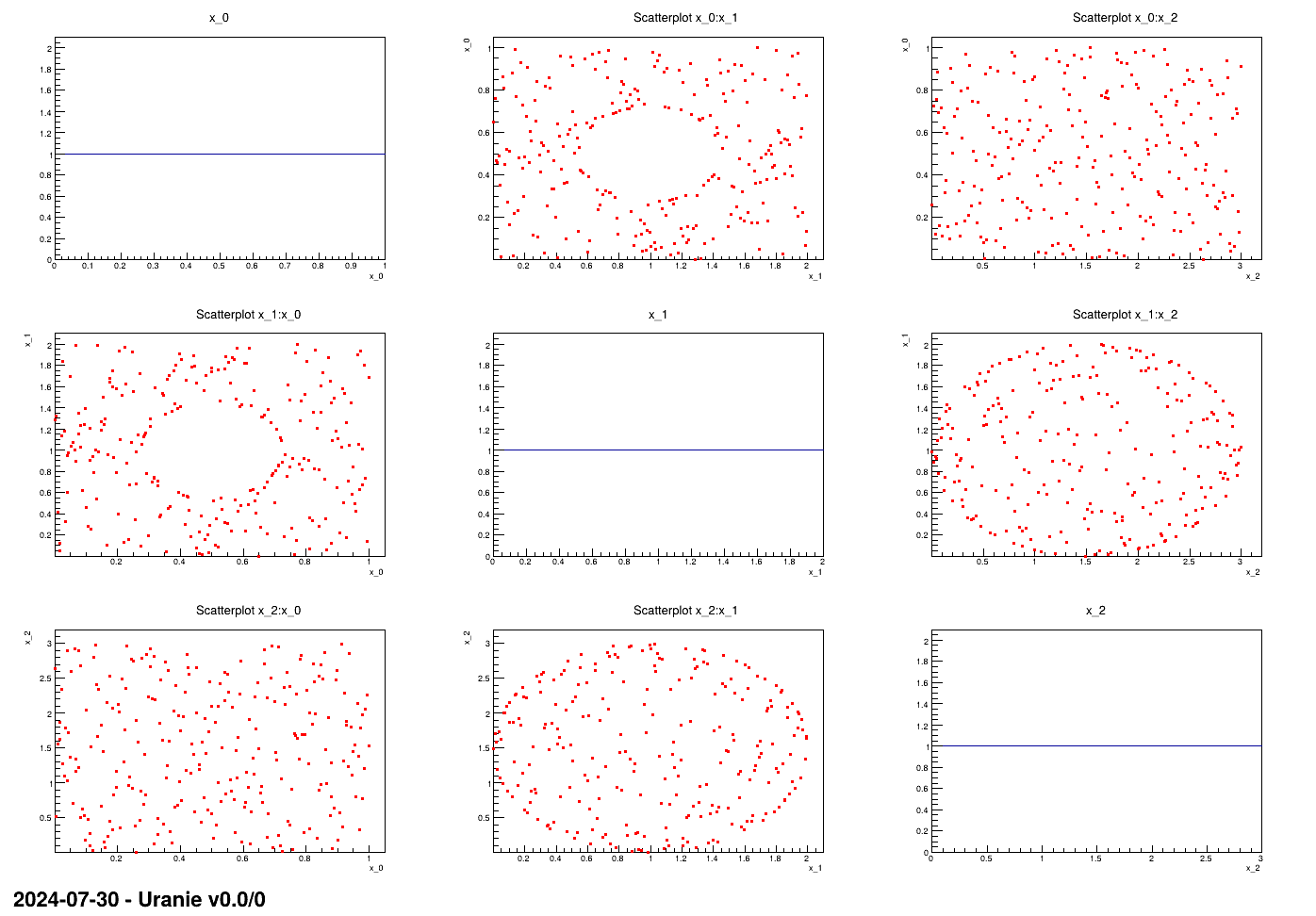
This macro shows the usage of the TConstrLHS class when one wants to create a constrained LHS with non-linear constraints. In order to illustate the concept, it is applied on three input variables drawn from uniform distribution with well-thought boundaries (as the concept of the LHS is to have nicely distributed marginals). The constraints are excluding the inner part of an ellipse for one of the input plane and the outter part of another ellipse for another input plane.

#include "ConstrFunctions.C"

void nicegrid(TDataServer *tds, TCanvas *Can)
{
    int ns=tds->getNPatterns(), nx=tds->getNAttributes();
    tds->drawPairs();
    TH1F *h[nx];
    TAttribute *att=NULL;
    gStyle->SetOptStat(0);
    for(int iatt=0; iatt<nx; iatt++)
    {
        Can->GetPad(iatt*(nx+1)+1)->cd();
        att=tds->getAttribute(iatt);
        h[iatt] = new TH1F(Form("%s_histo",att->GetName()), Form("%s_histo;x_%i",att->GetName(), iatt), ns, att->getLowerBound(), att->getUpperBound());
        tds->Draw(Form("%s>>%s_histo", att->GetName(), att->GetName()),"","goff");
        h[iatt]->Draw();
    }
}

int samplingConstrLHSEllipses()
{
    // Canvas to produce the 2x1 plot to compare LHS designs
    TCanvas *Can = new TCanvas("Can","Can", 10, 32, 1000, 1000);
    
    int ns = 250, nx = 3; // Size of the samples to be produced
    // Create dataserver and define the attributes
    TDataServer *tds = new TDataServer("tds","pouet");
    for(int iatt=0; iatt<nx; iatt++)
    {        
        tds->addAttribute( new TUniformDistribution(Form("x_%i",iatt),0,iatt+1) );
        tds->getAttribute(Form("x_%i",iatt))->delShare(); 
    }
    
    // Generate the constr lhs
    TConstrLHS *constrlhs = new TConstrLHS(tds, ns);
    vector<int> inputs = {1,0,1,2};
    constrlhs->addConstraint(CircularRules, 2, inputs.size(), &inputs[0]);
    constrlhs->generateSample();

    // Do the plot 
    nicegrid(tds, Can);
  
    return 0;
}

The very beginning of these macros is the nicegrid method which is here only to show the nice marginal distributions and the scatter plots. One can clearly skip this part to focus on the rest in the main function.

The macro very much looks like any other design-of-experiments generating macro above: the dataserver is created along with the canvas object and the problem is defined along with the input variables and the number of locations to be produced. Once done, then the TConstrLHS instance is created with the four following lines:

// Generate the constr lhs
TConstrLHS *constrlhs = new TConstrLHS(tds, ns);
vector<int> inputs = {1,0,1,2};
constrlhs->addConstraint(CircularRules, 2, inputs.size(), &inputs[0]);
constrlhs->generateSample();          
          

The constructor is pretty obvious, as it takes only the dataserver object and the number of locations. Once created the main method to be called is the addConstraint function which has been largely discussed in Section III.2.4. The first argument of this method is the pointer to the C++ function which has been included in our macro through the very first line:

#include "ConstrFunctions.C"

which contains the CircularRules function. The rest of the argument are the number of constraints, the size of the list of parameters and its content. Finally the nicegrid method is called to produce the nice plot shown in Figure XIV.15

This macro shows the usage of the SVD decomposition for the specific case where the target correlation matrix is singular. The idea is to provide a tool that will allow the user to compare quickly both the TSampling and TBasicSampling implementation, with a singular correlation matrix, or not. In order to do that, a toy random correlation matrix generator is provided.

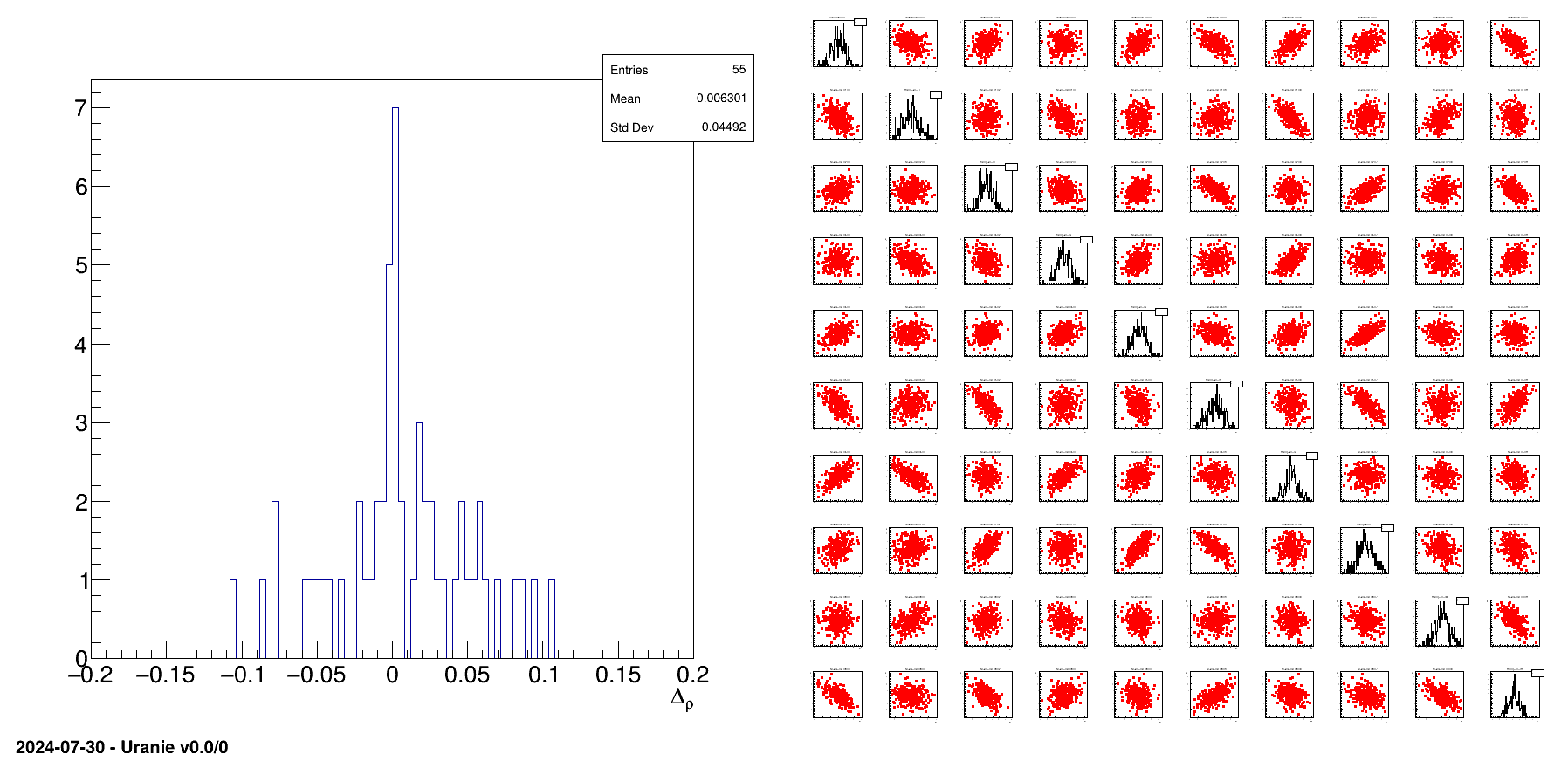
The resulting design-of-experiments is presented side-by-side with the residual of the obtained correlation matrix.

{
    // What classes to be used (true==TSampling, false==TBasicSampling)
    bool ImanConover=false; 
    TString SamplingType="srs";
    TString SamplerOption="svd"; // Remove svd to use Cholesky

    // Generating randomly a singular correlation matrix
    // dimension of the  problem in total.
    int n = 10; 
    // number of dimension self explained.
    // SHOULD BE SMALLER (singular) OR EQUAL TO (full-rank) n.
    int p = 6; 
    // number of location in the doe
    int m=300;

    // =========================================================================
    //          Internal recipe to get this correlation matrix
    // =========================================================================
    TMatrixD A(n,p);
    TRandom3 *Rand = new TRandom3(); 
    for(int i=0;i<n;i++){
        for(int j=0;j<p;j++){
            A(i,j) = Rand->Gaus(0.,1.);
        }
    }

    TMatrixD Gamma(A,TMatrixD::kMultTranspose,A);
    Gamma*=1./n;

    TMatrixD Sig(n,n);
    for(int i=0;i<n;i++) Sig(i,i)=1./sqrt( Gamma(i,i) );

    TMatrixD Corr(Sig,TMatrixD::kMult, Gamma);
    Corr*=Sig;
    // =========================================================================
    //                    Corr is our correlation matrix.
    // =========================================================================

    // Creating the TDS
    TDataServer *tds = new TDataServer("pouet","pouet");

    // Adding attributes
    for(int i=0;i<n;i++) tds->addAttribute( new TNormalDistribution(Form("n%d",i),0.,1.) );
    
    // Create the sampler and generate the doe
    if(ImanConover){
        TSampling *sam = new TSampling(tds,SamplingType.Data(),m); 
        sam->setCorrelationMatrix(Corr);
        sam->generateSample(SamplerOption.Data());
    }else{
        TBasicSampling *sam = new TBasicSampling(tds,SamplingType.Data(),m); 
        sam->setCorrelationMatrix(Corr);
        sam->generateCorrSample(SamplerOption.Data());
    }

    // Compute the empirical correlation matrix
    TMatrixD ResultCorr=tds->computeCorrelationMatrix();
    // Change it into a residual matrix
    ResultCorr-=Corr;

    gStyle->SetOptStat(1110);
    // Plot the results
    TCanvas *c=new TCanvas("c","c",1800,900);
    TPad *apad=new TPad("apad","apad",0, 0.03, 1, 1); apad->Draw(); apad->cd();
    apad->Divide(2,1);
    apad->cd(1);
    // Residual distribution
    TH1F *h=new TH1F("h",";#Delta_{#rho}",100,-0.2,0.2);
    for(int i=0;i<n;i++)
    {
        for(int j=i;j<n;j++) h->Fill(ResultCorr(i,j));
    }
    h->Draw();

    // all variables
    apad->cd(2);
    tds->drawPairs();
     
}

This macro starts by a bunch of variables provided to offer many possible configuration, among which:

This is the main part of this macro

 // What classes to be used (true==TSampling, false==TBasicSampling)
bool ImanConover=false; 
TString SamplingType="srs";
TString SamplerOption="svd"; // Remove svd to use Cholesky

// Generating randomly a singular correlation matrix
// dimension of the  problem in total.
int n = 10; 
// number of dimension self explained.
// SHOULD BE SMALLER (singular) OR EQUAL TO (full-rank) n.
int p = 6; 
// number of location in the doe
int m=300;

Once this is settled, the correlation matrix is created and the dataserver is created and n centered-reduced normal attributes are added. The chosen design-of-experiments is generated with the chosen options:

// Create the sampler and generate the doe
if(ImanConover){
TSampling *sam = new TSampling(tds,SamplingType.Data(),m);
sam->setCorrelationMatrix(Corr);
sam->generateSample(SamplerOption.Data());
}else{
TBasicSampling *sam = new TBasicSampling(tds,SamplingType.Data(),m);
sam->setCorrelationMatrix(Corr);
sam->generateCorrSample(SamplerOption.Data());
}

Finally the obtained design-of-experiments is shown along with the residual of all the correlation coefficients (difference between the target values and the obtained ones). This is shown in Figure XIV.16 and can be used to compare the performance of the samplers.