Documentation
/ User's manual in Python
: 
| II.6. Combining these aspects: performing PCA | ||
|---|---|---|
 | Chapter II. The DataServer module |  |
This part is introducing an example of analysis that combines all the aspects discussed up to now: handling data, perform a statistical treatment and visualise the results. This analysis is called PCA for Principal Component Analysis and is often used to
gather event in a sample that seem to have a common behaviour;
reduce the dimension of the problem under study.
There is a very large number of articles, even books, discussing the theoretical aspects of principal component analysis (for instance one can have a look at [jolliffe2011principal]) a small theoretical introduction can in any case be found in [metho].
Let's use a relatively simple example to illustrate the principle and the way we can achieve a reduction of
dimension while keeping the inertia as large as possible. One can have a look at a sample of marks from different
pupils, in various kinds of subject, all gathered in the Notes.dat whose content is shown
below.
#TITLE: Marks of my pupils
#COLUMN_NAMES: Pupil | Maths | Physics | French | Latin | Music
#COLUMN_TYPES: S|D|D|D|D|D
Jean 6 6 5 5.5 8
Aline 8 8 8 8 9
Annie 6 7 11 9.5 11
Monique 14.5 14.5 15.5 15 8
Didier 14 14 12 12 10
Andre 11 10 5.5 7 13
Pierre 5.5 7 14 11.5 10
Brigitte 13 12.5 8.5 9.5 12
Evelyne 9 9.5 12.5 12 18
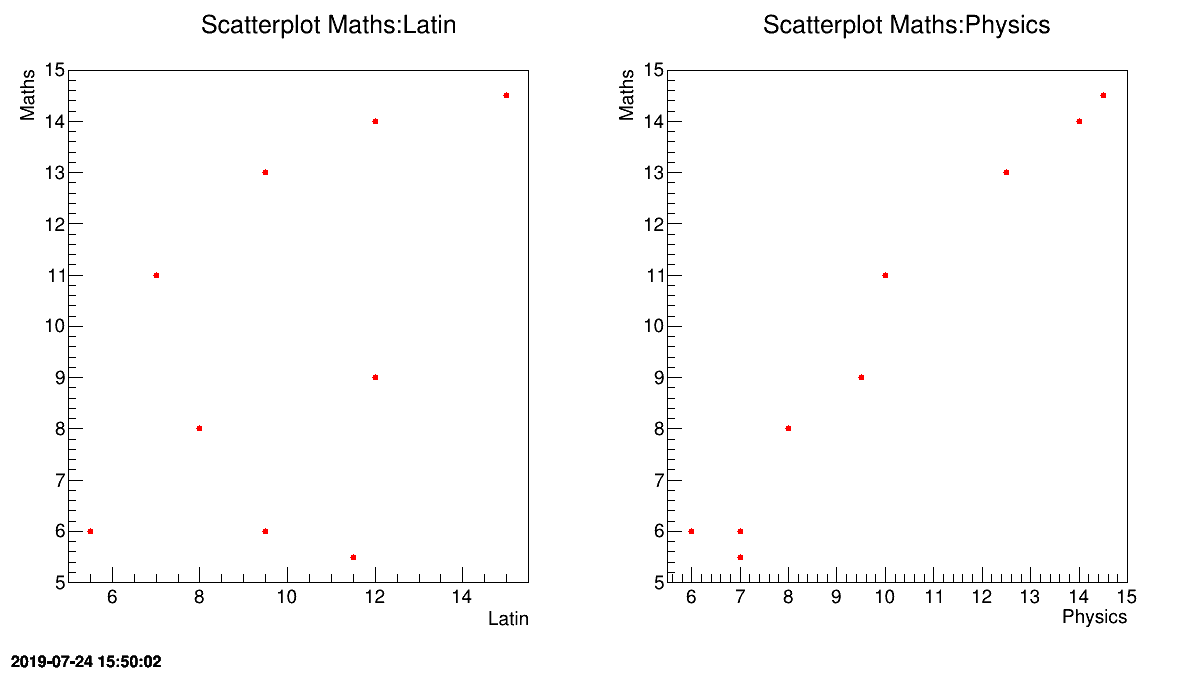
One can have a look at some of these variables against one another to have a sense of what's about to be done. In Figure II.54, the maths marks of the pupils are displayed against latin on the left and physics on the right. Whereas no specific trend is shown on the left part, an obvious correlation can be seen from the right figure meaning one can try extrapolate the maths marks from the value of the physics one.
The way to perform this analysis is rather simple through Uranie: simply provide the dataserver that
contains data to an TPCA object, only precising the name of the variables to be
investigated. This is exactly what's done below:
# Read the database
tdsPCA = DataServer.TDataServer("tdsPCA", "my TDS")
tdsPCA.fileDataRead("Notes.dat")
# Create the PCA object precising the variables of interest
tpca = DataServer.TPCA(tdsPCA, "Maths:Physics:French:Latin:Music")
tpca.compute()Once done, the process described in the [metho] is finished and then interpretation starts.
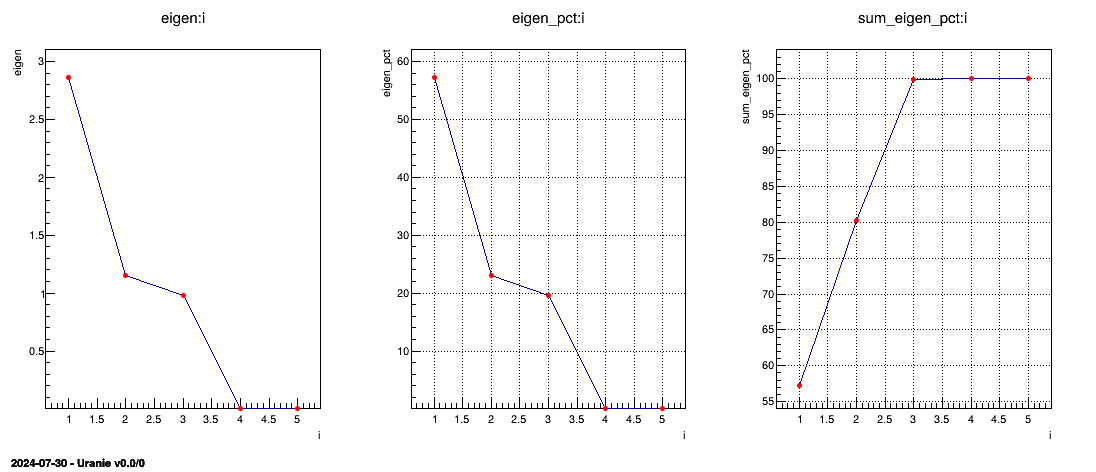
The first result that one should consider is the non-zero eigenvalues (so the variance of the corresponding
principal components). These values are stored in a specific ntuple, that can be retrieve by calling the method
getResultNtupleD(). This ntuple contains three kind of information: the eigenvalues itself
("eigen"), these values as contributions in percent of the sum of eigenvalues
("eigen_pct") and the sum of these contributions ("sum_eigen_pct").
All these values can be accessed through the usual Scan method (see Section XIV.3.17 to see the results).
The following lines are showing how to represent the eigenvalues as plots and the results are gathered in Figure II.55. From this figure, one can easily conclude that only the three first principal components are useful (as it reached an inertia of a bit more than 99% of the original one). This is the solution chosen for the rest of the graphical representations below and this is the first nice results from this step: it is possible to reduce the dimension of our problem from the 5 different subjects to the three principal component that needs to be explicated.
# Draw the eigen values in different normalisation
c = ROOT.TCanvas("cEigenValues", "Eigen Values Plot",1100,500)
apad3 = ROOT.TPad("apad3","apad3",0, 0.03, 1, 1)
apad3.Draw()
apad3.cd()
apad3.Divide(3,1)
ntd = tpca.getResultNtupleD()
apad3.cd(1)
ntd.Draw("eigen:i","","lp")
apad3.cd(2)
ntd.Draw("eigen_pct:i","","lp")
ROOT.gPad.SetGrid()
apad3.cd(3)
ntd.Draw("sum_eigen_pct:i","","lp")
ROOT.gPad.SetGrid()
c.SaveAs("PCA_notes_musique_Eigen.png")
Figure II.55. Representation of the eigenvalues (left) their overall contributions in percent (middle) and the sum of the contributions (right) from the PCA analysis.
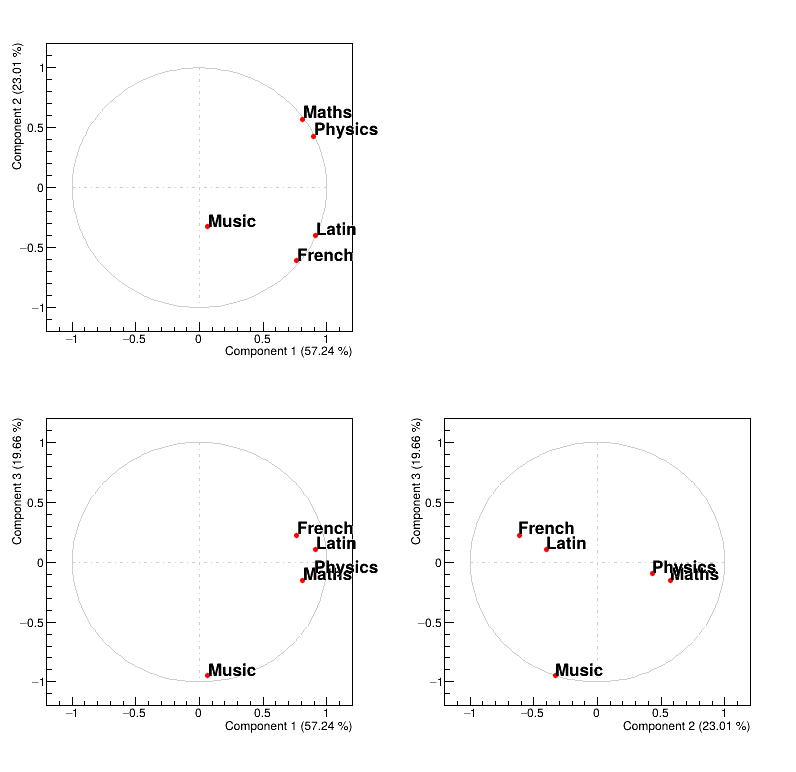
As stated previously, one can have a look at the variables in their usual representation (that can be seen in
Figure II.56) that is called the correlation circle. This plot is obtained by
calling the drawLoading method that takes two arguments: the first one being the number
of the PC used as x-axis while the second one is the number of the PC used as y-axis. The code to get Figure II.56 is shown below:
# Draw all variable weight in PC definition
cLoading = ROOT.TCanvas("cLoading", "Loading Plot",800,800)
apad2 = ROOT.TPad("apad2","apad2",0, 0.03, 1, 1)
apad2.Draw()
apad2.cd()
apad2.Divide(2,2)
apad2.cd(1)
tpca.drawLoading(1,2)
apad2.cd(3)
tpca.drawLoading(1,3)
apad2.cd(4)
tpca.drawLoading(2,3)Figure II.56 represents the correlation between the original variable and the principal component under study. Two kinds of principal component are resulting from PCA:
the size one where all variables are on the same size of the principal component. In our case, the first PC in Figure II.56 represents the variability of marks.
the shape one where variables are balanced from positive to negative value of the principal component. In our case, the second PC in Figure II.56 represents the difference observed between scientific variables, such as maths and physics, from literary ones, such as french and latin.
Finally to complete the picture, the third PC is a shape one that represents the fact that music seems to have a very specific behaviour, different from all the other studies.
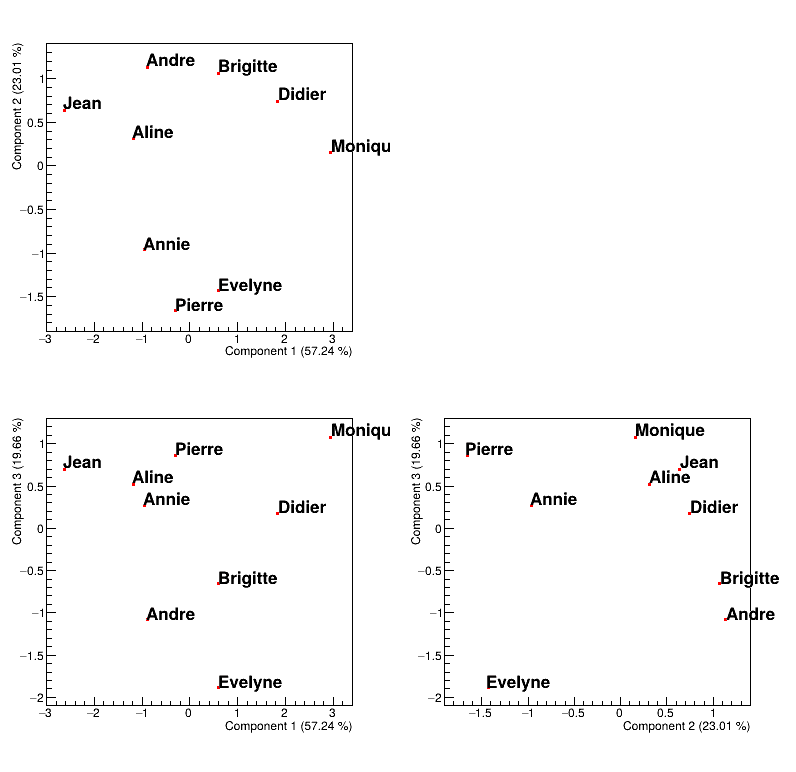
Finally, one can also have a look at the points distribution in the new PC space (that can be seen in Figure II.57). This plot is obtained by calling the method drawPCA that
takes two compulsory arguments: the first one being the number of the PC used as x-axis while the second one is
the number of the PC used as y-axis. An extra argument can be provided that is used to specify a branch in the
database that contains the name of the points (the name of the pupils) which allows to get a nice final plot. The
code to get Figure II.57 is shown below:
# Draw all point in PCA planes
cPCA = ROOT.TCanvas("cpca", "PCA",800,800)
apad1 = ROOT.TPad("apad1","apad1",0, 0.03, 1, 1)
apad1.Draw()
apad1.cd()
apad1.Divide(2,2)
apad1.cd(1)
tpca.drawPCA(1,2,"Pupil")
apad1.cd(3)
tpca.drawPCA(1,3,"Pupil")
apad1.cd(4)
tpca.drawPCA(2,3,"Pupil")Figure II.57 shows where to find our pupils with respect to our new basis and the interpretation of the correlation plot of the variable holds as well:
looking at PC1, it seems to be defined by two extremes, Jean and Monique, the former being bad at every subjects while the latter is good at (almost) all subjects.
looking at PC2, it also seems to be defined by two extremes, Pierre and Andre, the former having way better marks at literary subjects than at scientific ones while its the other way around for the latter.
looking at PC3, it seems to oppose Evelyn to all the other pupils, and this correspond to fact that every pupils is bad at music, but Evelyn.
All these interpretations remain graphical and give an easy way to summarise the impact of the PCA analysis. Disregarding the sources considered (the variables or the points), one can have quantitative interpretation coefficients that detail more the "feeling" described above:
the quality of the representation: it shows how well the source (either the subject or the pupil in our case) is represented by a given PC. Summing these values over the PC should lead to 1 for every sources.
the contribution to axis: it shows how much the source (either the subject or the pupil in our case) contribute to the definition of the given PC. Summing these values over the source (for the given PC) should lead to 1 for every PC.
Example of how to get these numbers can be found in the use-case macros, see Section XIV.3.17.
| |  | |
| II.5. Visualisation dedicated to uncertainties |  | Chapter III. The Sampler module |