Documentation
/ Manuel utilisateur en Python
: 
| V.6. The kriging method | ||
|---|---|---|
 | Chapter V. The Modeler module |  |
Warning
This surrogate model, as implemented in Uranie, requires the NLopt prerequisite (as discussed in Section I.1.2.2).
First developed for geostatistic needs, the kriging method, named after D. Krige and also called Gaussian Process method (denoted GP hereafter) is another way to construct a surrogate model. It recently became popular thanks to a series of interesting features:
it provides a prediction along with its uncertainty, which can then be used to plan the simulations and therefore improve the predictions of the surrogate model
it relies on relatively simple mathematical principle
some of its hyper-parameters can be estimated in a Bayesian fashion to take into account a priori knowledge.
Kriging is a family of interpolation methods developed in the 1970s for the mining industry [Matheron70]. It uses information about the "spatial" correlation between observations to make predictions with a confidence interval at new locations. In order to produce the prediction model, the main task is to produce a spatial correlation model. This is done by choosing a correlation function and search for its optimal set of parameters, based on a specific criterion.
The gpLib library [gpLib] provides tools to achieve this task. Based on the gaussian process properties of the kriging [bacho2013], the library proposes various optimisation criteria and parameter calculation methods to find the parameters of the correlation function and build the prediction model.
The present chapter describes the integration of the gpLib inside Uranie, and how to create a new kriging model and use it. We first give a quick reminder of what kriging is. Next, we describe how to create a new prediction model using Uranie. Then, we explain how to use this model to predict new observations. Finally, we present some advanced usages of the Uranie/gpLib interface.
The aim of developing a meta-model is to emulate a code or a function which takes a certain number of inputs (that one
can write like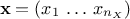 
) and gives a scalar 
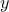as a result. If one has a set of 
measurements, meaning that the relation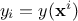 
is perfectly known for 
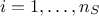, the gaussian process model can be used
to re-estimate the observations and provide an expected value for new measurements.
The kriging procedure in Uranie can be schematised in five steps, depicted in Figure V.4 and an example can be found in Section XIV.7.14. As for the
polynomial chaos expansion discussed in Section V.3, the classes are mainly interfaces,
here to the classes extracted from the gpLib library. Here is a brief description of
the steps:
get a training site. Either produced by a design-of-experiments from a model definition, or taken from anywhere else, it is mandatory to get this basis (the larger, the better).
define the kriging options. This is heavily discussed in Section V.6.2, all the options discussed in the aforementioned section will be inputs of the
TGPBuilderclass that will be build the kriging model.set the parameter's values. It can be set by hands, but it is highly recommended to proceed through an optimisation, to get the best possible parameters.
build the kriging method. This is done with a specific method of
TGPBuilderwhich returns aTKrigingobject. This object is the one that would be saved (if requested) and used to perform the next step.test the obtained kriging model. This is done by running the kriging model over a new basis (the test one) using a
TLauncher2object (which is the equivalent of aTLauncherbut from the URANIE::Relauncher module). This module will be discussed later on in Chapter VIII. With this approach, a one-by-one estimation of the prediction is performed. To get the complete prediction with the new location covariance matrix (see [metho] for this theory behind this discussion) a different method has been introduced, see Section V.6.3.2.
The Uranie wrapper to the gpLib is based on 4 main classes:
TGPBuilder: allow to search for the optimal parameters of the correlation function and to build the kriging model;TCorrelationFunction: parent class of the correlation functions used to model the spatial correlation of the observations;TGPCostFunction: parent class of the criteria used to find the optimal parameters of the correlation function;TKriging: used to predict new values (with confidence interval).
Most of the time, users will only need to use the TGPBuilder
and TKriging classes.
The example code below creates a prediction model of the type "simple kriging" (it can be found in Section XIV.7.9).
"""
Example of Gaussian Process building
"""
from rootlogon import DataServer, Modeler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern3/2") # name of the correlation function
# Search for the optimal hyper-parameters
gpb.findOptimalParameters("ML", # optimisation criterion
100, # screening design size
"neldermead", # optimisation algorithm
500) # max. number of optim iterations
# Construct the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
In this script, after loading the observation data into a dataserver, we create a
TGPBuilder object. To do so, one should provide the observations, the name of the attributes
corresponding to the inputs, the name of the attribute corresponding to the output, and the name of the correlation
function (here, it is a Matern 3/2 correlation function. The training
(utf_4D_train.dat) and testing (utf_4D_test.dat) database can both be found
in the document folder of the Uranie installation (${URANIESYS}/share/uranie/docUMENTS). Please
refer to Table V.6 or [metho] for the list of available
correlation functions).
The next step is to find the optimal parameters of the correlation function. To achieve this, we can use the
TGPBuilder::findOptimalParameters function. It is a "helper function" where all the tedious work
is done automatically. The drawback is that the user cannot modify some properties (parameters range, optimisation
precision, etc.), or use some interesting features of Uranie (non-random sampling, evolutionary optimisation
algorithms, distributed computing, etc.). Section V.6.4 gives some
examples of how to search for optimal parameters without using the function
findOptimalParameters.
The search for the optimal parameters requires the user to choose:
- an optimisation criterion (in the example: the Maximum likelihood);
- the size of the screening design-of-experiments;
- an optimisation algorithm;
- a maximum number of optimisation runs.
The search for optimal parameters will start by the search of a "good" starting point for the optimisation. This is done by evaluating the criterion on a LHS design-of-experiments of the input space. This "screening" procedure is optional and can be skipped by setting the design size to 0.
The optimisation procedure will start either at the "best" location found by the screening, or at a default location. The chosen optimisation algorithm is then used to search for an optimal solution. Depending on various conditions, convergence can be difficult to achieve. The number of optimisation runs is thus limited to 1000 by default, but can be increased or decreased by the user. The list of available optimisation criteria is available in Table V.4. The list of optimisation algorithms is available in Table V.5. You can also refer to the developer documentation.
When the search is finished, and if everything went well, we can create a kriging model using the function
TGPBuilder::buildGP. This function returns the pointer to a TKriging
object which can be used for the prediction of new points. The function TKriging::printLog
shows some of the properties of the model, like the parameters of the correlation function and the leave one out
performances (RMSE and Q2):
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
1.6181e+00 (1.6172e+00 )
1.4372e+00 (1.4370e+00 )
1.5026e+00 (1.5009e+00 )
6.7884e+00 (6.7944e+00 )
Variance of the gaussian process: 70.8755
RMSE (by Leave One Out): 0.499108
Q2: 0.849843
*******************************
Warning
Internally, the inputs are automatically normalised to the interval [0, 1]. As a consequence, the "normalised" correlation lengths correspond to distances in the normalised space, and the "not normalised" lengths correspond to distances in the original space.
Sometimes, the optimisation fails due to an ill-conditioned covariance matrix. The corresponding cost is set to an absurd value and this is signalled, at the end, by a warning message of the form (when XX estimations fail out of the total number TOT):
<WARNING> TGPBuilder::Screening procedure. The Cholesky decomposition has failed XX out of TOT times </WARNING>
It can then be useful to apply a regularisation parameter (mathematically similar to the "nugget effect" of geostatistics).
To apply the regularisation, we simply have to write:
gpb.setRegularisation(1e-6)
before calling findOptimalParameters. Typical values for the regularisation parameter lie
between 1e-12 and 1e-6.
Defining a deterministic trend is done at the construction of the TGPBuilder object. It can be
generated automatically by using a keyword ("const" or "linear")
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern3/2", # name of the correlation function
"linear") # trend defined by a keywordor manually by writing a formula where the terms are separated by colon character (":")
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern3/2", # name of the correlation function
"1:x1:x2+x4^2") # custom trend
When using the "const" keyword, the trend is a constant value. When using "linear", the trend is a linear combination of all the normalised input variables (plus a constant).
When using a formula, each sub-element must be either a constant or a combination of one or more inputs. It must also respect ROOT's formula syntax (cf. TFormula description for details).
Warning
Custom trend applies on "original space" variables, while automatic trend applies on "normalised space" variables.
This shows the impact of all deterministic trend cases implementation:
"": no trend given.
"const": There is an extra parameter
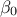to determine, as 
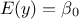."linear": There are
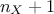extra parameters to be determined, as 
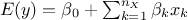. "a:b:c": This is customised trend. The given string is split according to ":". There will be as many new parameters as there are entries and "a", "b", and "c" can be functions of various input variables. For instance with a line like
,
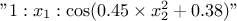the trend would be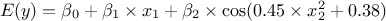 
If we have an a priori knowledge on the mean and variance of the trend parameters, we can use it to perform a bayesian study, as in the example below (which can be found in Section XIV.7.11):
"""
Example of Gaussian Process building with a priori knowledge
"""
import numpy as np
from rootlogon import DataServer, Modeler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern3/2", # name of the correlation function
"linear") # trend defined by a keyword
# Bayesian study
meanPrior = np.array([0.0, 0.0, -1.0, 0.0, -0.1])
covPrior = np.array([1e-4, 0.0, 0.0, 0.0, 0.0,
0.0, 1e-4, 0.0, 0.0, 0.0,
0.0, 0.0, 1e-4, 0.0, 0.0,
0.0, 0.0, 0.0, 1e-4, 0.0,
0.0, 0.0, 0.0, 0.0, 1e-4])
gpb.setPriorData(meanPrior, covPrior)
# Search for the optimal hyper-parameters
gpb.findOptimalParameters("ReML", # optimisation criterion
100, # screening design size
"neldermead", # optimisation algorithm
500) # max. number of optim iterations
# Construct the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
Warning
Please note that we change the optimisation criterion from "ML" (Maximum likelihood) to "ReML" (Restricted Maximum likelihood) as the former cannot handle bayesian studies.
The information displayed by the TKriging::printLog function shows the values of the 5
trend parameters calculated by the bayesian study. The a priori variance of the parameters being
very small, we can see that the trend parameters are very close to their a priori means.
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend: linear
Trend parameters (5): [3.06586494e-05; 1.64887174e-05; -9.99986787e-01; 1.51959859e-05; -9.99877606e-02 ]
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
2.1450e+00 (2.1438e+00 )
1.9092e+00 (1.9090e+00 )
2.0062e+00 (2.0040e+00 )
8.4315e+00 (8.4390e+00 )
Variance of the gaussian process: 155.533
RMSE (by Leave One Out): 0.495448
Q2: 0.852037
*******************************
Tip
If you want to deactivate the bayesian mode after setting the prior data, call
gpb->setUsePrior(kFALSE) before searching for the optimal parameters. You can reactivate the
bayesian mode later by calling gpb->setUsePrior(kTRUE).
If we want to take a measurement error into account when looking for the optimal hyper-parameters, we can do so by calling the function:
gpb.setHasMeasurementError(True)The measurement error is supposed to follow a normal law of mean 0. If the variance vMes is unknown, a new parameter alpha = vMes/vGP (where vGP is the variance of the gaussian process) will be added to the list of hyper-parameters to optimise.
If we know the variance of the measurement error to be a constant, it must be set using the function
vMes = 0.0025
gpb.setMeasurementErrorVariance(vMes)We may even know the covariance matrix of a complex measurement error. In such case, it must be set using the function
import numpy as np
covMes = np.array([25*1e-4, 0.0, 0.0, 0.0, 0.0,
0.0, 25*1e-4, 0.0, 0.0, 0.0,
0.0, 0.0, 25*1e-4, 0.0, 0.0,
0.0, 0.0, 0.0, 25*1e-4, 0.0,
0.0, 0.0, 0.0, 0.0, 25*1e-4])
gpb.setMeasurementErrorCovMatrix(covMes)In both cases, the variance of the gaussian process, which is otherwise determined analytically from the other hyper-parameters, becomes one of the hyper-parameters to optimise.
The optimisation phase of the search for optimal parameters depends on the choice of a criterion and an optimisation algorithm. In the tables below, we present a quick description of the available options.
Table V.4. Optimisation criteria
| Criteria | keyword | no trend | trend | bayesian | description |
|---|---|---|---|---|---|
| Maximum likelihood | ML | yes | yes | no | Look for the hyper-parameters which maximise the density of the gaussian vector of the observation outputs. It cannot be used for bayesian studies. |
| Restricted Maximum likelihood | ReML | no | yes | yes | Same as ML, but adapted to allow bayesian studies. It cannot be used without a trend. |
| Leave One Out | Loo | yes | yes | yes | Thanks to the linear nature of the kriging model, the Leave One Out error has an analytic formulation. It can be used as a quality criterion. |
Table V.5. Optimisation algorithm
| Algorithm | keyword | Use gradient | description |
|---|---|---|---|
| Nelder-Mead Simplex | NelderMead | no | This is an implementation of the "simplex" algorithm, simple and quite efficient in most cases. However, it does not always converge to a local minimum |
| Subplex | Subplexe[a] | no | Another version of the simplex supposed to be more robust and efficient than Nelder-Mead |
| Constrained Optimisation By Linear Approximations | Cobyla | no | Construct successive linear approximations of the cost function (using a simplex) and optimise them. |
| Bound Optimisation BY Quadratic Approximation | Bobyqa | no | Construct quadratic approximations of the cost function and optimise them. May perform poorly on cost function that are not twice-differentiable ! |
| Principal Axis | Praxis | no | Use the "principal axis" method to converge to a solution without estimating a gradient. May be slow to converge. |
| Low-storage BFGS | BFGS | yes | An improved implementation of the BFGS algorithm which reduces memory consumption and convergence time. |
| Preconditioned truncated Newton | Newton | yes | An implementation of the Newton algorithm which reduces memory consumption and convergence time. |
| Method of Moving Asymptotic | MMA | yes | Construct local approximation of the cost function based on the gradient, the constraints and a quadratic "penalty" term. The approximation obtained is "easy" to optimise. This algorithm is guaranteed to converge to a local minimum whatever the starting point. |
| Sequential Least-Squares Quadratic Programming | SLSQP | yes | The algorithm optimises successive second-order approximations of the cost function (via BFGS updates), with first-order (linear) approximations of the constraints. As it uses "true" BFGS, this algorithm becomes slow for large numbers of parameters |
| Shifted limited-memory variable-metric | VariableMetric | yes | This algorithm is adapted to large scale optimisation problems. |
[a] the additional "e" is to respect the original author's wish that only his implementation of the algorithm be named "Subplex". | |||
For more details about the algorithms, please consult the NLopt website ( http://ab-initio.mit.edu/wiki/index.php/NLopt_Algorithms).
In the examples presented so far, the initial point of the optimisation procedure was either a default location or determined via a random sampling of the input space. If a specific location is needed, it can be set as shown below (which can be found in Section XIV.7.10):
"""
Example of Gaussian Process building with initial point set
"""
import numpy as np
from rootlogon import DataServer, Modeler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, "x1:x2:x3:x4", "y", "matern3/2")
# Set the correlation function parameters
params = np.array([1.0, 0.25, 0.01, 0.3])
gpb.getCorrFunction().setParameters(params)
# Find the optimal parameters
gpb.findOptimalParameters("ML", # optimisation criterion
0, # screening size MUST be equal to 0
"neldermead", # optimisation algorithm
500, # max. number of optim iterations
False) # Don't reset parameters of GP builder
# Create the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
In this case, only the initial correlation lengths need to be set, so we simply retrieve the pointer to the
correlation function object and use the setParameters function. Then, we call
findoptimalParameters with two particularities:
the screening size must be set to 0, otherwise the initial point will be defined as the best location of a random sampling;
the last parameter of the function, called "reset", must be set to
kFALSE. This insures that the current values of the hyper-parameters are not reset to their default values.
Warning
When setting the correlation lengths manually, remember that the values you provide are considered normalised.
The resulting model is printed as follow:
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
1.6182e+00 (1.6173e+00 )
1.4373e+00 (1.4371e+00 )
1.5027e+00 (1.5011e+00 )
6.7895e+00 (6.7955e+00 )
Variance of the gaussian process: 70.8914
RMSE (by Leave One Out): 0.49911
Q2: 0.849842
*******************************
One situation where it might be interesting to continue an optimisation procedure from the last optimal solution found is when the observation dataset is updated "on the fly". A typical use-case is the iterative construction of a design-of-experiments.
If the contents of the dataserver of the observations are modified, we must update the internal matrices of the
TGPBuilder, but without modifying the hyper-parameters we have found so far. The function
TGPBuilder::updateObservations does exactly that:
"""
Example of GP model update with new data
"""
import numpy as np
from rootlogon import DataServer, Modeler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, "x1:x2:x3:x4", "y", "matern3/2")
# Search for the optimal hyper-parameters
gpb.findOptimalParameters("ML", 100, "neldermead", 500)
# Create a new observation
newObs = np.array([tdsObs.getNPatterns()+1, 7.547605e-01, 8.763968e-01,
1.255390e-01, 6.370434e-01, 1.189220e+00])
tdsObs.getTuple().Fill(newObs)
# Update the GP Builder
gpb.updateObservations()
# Search for optimal hyper-parameters, starting from their current values
gpb.findOptimalParameters("ML", 0, "bobyqa", 500, False)
# Create the model
krig = gpb.buildGP()
# Display model information
krig.printLog()
The resulting model is printed as follow:
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
1.6272e+00 (1.6263e+00 )
1.4443e+00 (1.4441e+00 )
1.5095e+00 (1.5078e+00 )
6.8387e+00 (6.8447e+00 )
Variance of the gaussian process: 71.8595
RMSE (by Leave One Out): 0.498229
Q2: 0.85008
*******************************
In the following example, we use a newly constructed kriging model to estimate the output of a new dataset (the code can be found in Section XIV.7.12):
"""
Example of Gaussian Process building with estimation on another dataset
"""
from rootlogon import DataServer, Modeler, Relauncher
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern3/2") # name of the correlation function
# Search for the optimal hyper-parameters
gpb.findOptimalParameters("ML", # optimisation criterion
100, # screening design size
"neldermead", # optimisation algorithm
500) # max. number of optim iterations
# Construct the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
# Load the data to estimate
tdsEstim = DataServer.TDataServer("tdsEstim", "estimations")
tdsEstim.fileDataRead("utf_4D_test.dat")
# Construction of the launcher
lanceur = Relauncher.TLauncher2(tdsEstim, # data to estimate
krig, # model used
"x1:x2:x3:x4", # list of the input variables
"yEstim:vEstim") # name of model's outputs
# Launch the estimations
lanceur.solverLoop()
# Display some results
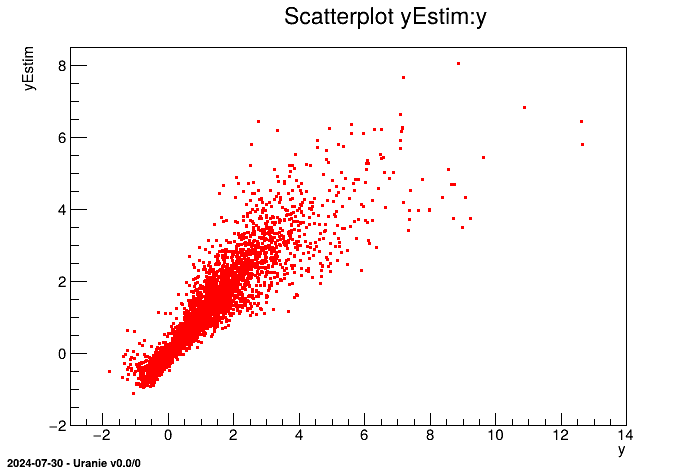
tdsEstim.draw("yEstim:y")
The part where the kriging model is constructed is identical to Section V.6.2.2.
After printing the model information, the new data are loaded into a dataserver. The TKriging
class is a children of TSimpleEval and can thus be used by a TMaster
(cf. Chapter VIII). Here, we create a TLauncher2 object. It
receives the data to estimate, the model to apply, the names of the input variables, and the names of the output
variable. The latter is added to the dataserver and receive the responses of the model when the function
solverLoop is called.
Warning
Using the prototype shown above (and recall here) to constructTLauncher2 instance is
perfectly fine as long as one does not want to use constant or temporary attributes. If you don't know what's
discussed here, we strongly invite you to have a look here Section VIII.5.1.
TLauncher2(tds, fun, in, out)TDataServer) but there is
no way to state that one input attribute is constant to set its value later-on just before the
solverLoop call. In order to do that, one should stick to the "classical" Relauncher architecture:
add input attributes to the evaluator using the
addInputand / orsetInputsmethods;add output attributes to the evaluator using the
addOutputand / orsetOutputsmethods;create the
TLauncher2instance with this prototypeTLauncher2(tds, fun)
For each point of the data set, we now have an estimation of the output ("yEstim") and a variance of this estimation ("vEstim"). We can access these values via the dataserver's visualisation or computation tools.
In the following example, we use a newly constructed kriging model to estimate the output of a new dataset, but unlike the previous case (see Section V.6.3.1) the prediction is done at once, taking into account the covariance of the new locations input to produce the prediction covariance matrix. The code can also be bound in Section XIV.7.13.
"""
Example of Gaussian Process building with estimation using full data (covariance)
"""
from rootlogon import ROOT, DataServer, Modeler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "observations")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, # observations data
"x1:x2:x3:x4", # list of input variables
"y", # output variable
"matern1/2") # name of the correlation function
# Search for the optimal hyper-parameters
gpb.findOptimalParameters("ML", # optimisation criterion
100, # screening design size
"neldermead", # optimisation algorithm
500) # max. number of optim iterations
# Construct the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
# Load the data to estimate
tdsEstim = DataServer.TDataServer("tdsEstim", "estimations")
tdsEstim.fileDataRead("utf_4D_test.dat")
# Reducing DB to 1000 first event (leading to cov matrix of a million value)
nS = 1000
tdsEstim.exportData("utf_4D_test_red.dat", "", "tdsEstim__n__iter__<="+str(nS))
# Reload reduced sample
tdsEstim.fileDataRead("utf_4D_test_red.dat", False, True)
krig.estimateWithCov(tdsEstim, # data to estimate
"x1:x2:x3:x4", # list of the input variables
"yEstim:vEstim", # name given to the model's outputs
"y", # name of the true reference
"DummyOption") # options
cTwo = None
# Produce residuals plots if true information provided
if tdsEstim.isAttribute("_Residuals_"):
cTwo = ROOT.TCanvas("c2", "c2", 1200, 800)
cTwo.Divide(2, 1)
cTwo.cd(1)
# Usual residual considering uncorrated input points
tdsEstim.Draw("_Residuals_")
cTwo.cd(2)
# Corrected residuals, taking full prediction covariance matrix
tdsEstim.Draw("_uncorrResiduals_")
# Retrieve all the prediction covariance coefficient
tdsEstim.getTuple().SetEstimate(nS*nS) # allocate the correct size
# Get a pointer to all values
tdsEstim.getTuple().Draw("_CovarianceMatrix_", "", "goff")
cov = tdsEstim.getTuple().GetV1()
# Put these in a matrix nicely created
Cov = ROOT.TMatrixD(nS, nS)
Cov.Use(0, nS-1, 0, nS-1, cov)
# Print it if size is reasonnable
if nS < 10:
Cov.Print()
The part where the kriging model is constructed is identical to Section V.6.2.2.
After printing the model information, the new data are loaded into a dataserver. Unlike the previous case (see Section V.6.3.1), the validation database is reduced to a fifth of its
original size, as the global approach will have to compute the input covariance matrix but also, from it, the
prediction covariance matrix, both of which have, just for the reduced case, a million coefficients.
The method to do this is called estimateWithCov and it can take 5 parameters:
a pointer to the dataserver;
the list of inputs to be used;
the name of the outputs. Only two are allowed and compulsory: the predicion and its conditional variance;
the name of the true value of the model (optional). Usable only with validation / test database;
and the options.
For each point of the data set, we now have an estimation of the output ("yEstim") and a variance of this estimation ("vEstim"). This method also produce few more attributes:
"_CovarianceMatrix_": this is a strange way to store the final prediction covariance matrix. It is a new vector attribute whose size is constant throughout the dataserver and it is the size of the sample. For every entry it corresponds to the row of the covariance matrix and the recommended way to extract it is the way shown above, i.e.
# Retrieve all the prediction covariance coefficient tdsEstim.getTuple().SetEstimate(nST * nST) # allocate the correct size # Get a pointer to all values tdsEstim.getTuple().Draw("_CovarianceMatrix_", "", "goff") cov = tdsEstim.getTuple().GetV1() # The data itself # Put these in a matrix nicely created (high level object to deal with) Cov = ROOT.TMatrixD(nST, nST) Cov.Use(0, nST-1, 0, nST-1, cov)"_Residuals_" and "_uncorrResiduals_": available only if the true value of the model is provided along (as fourth parameter of the function prototype). It is basically the following ratio for all locations in the tested database P:
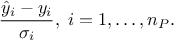
It is depicted in our case in Figure V.6.
Figure V.6. Residual distribution using a validation database with and without prediction covariance correction.
 |
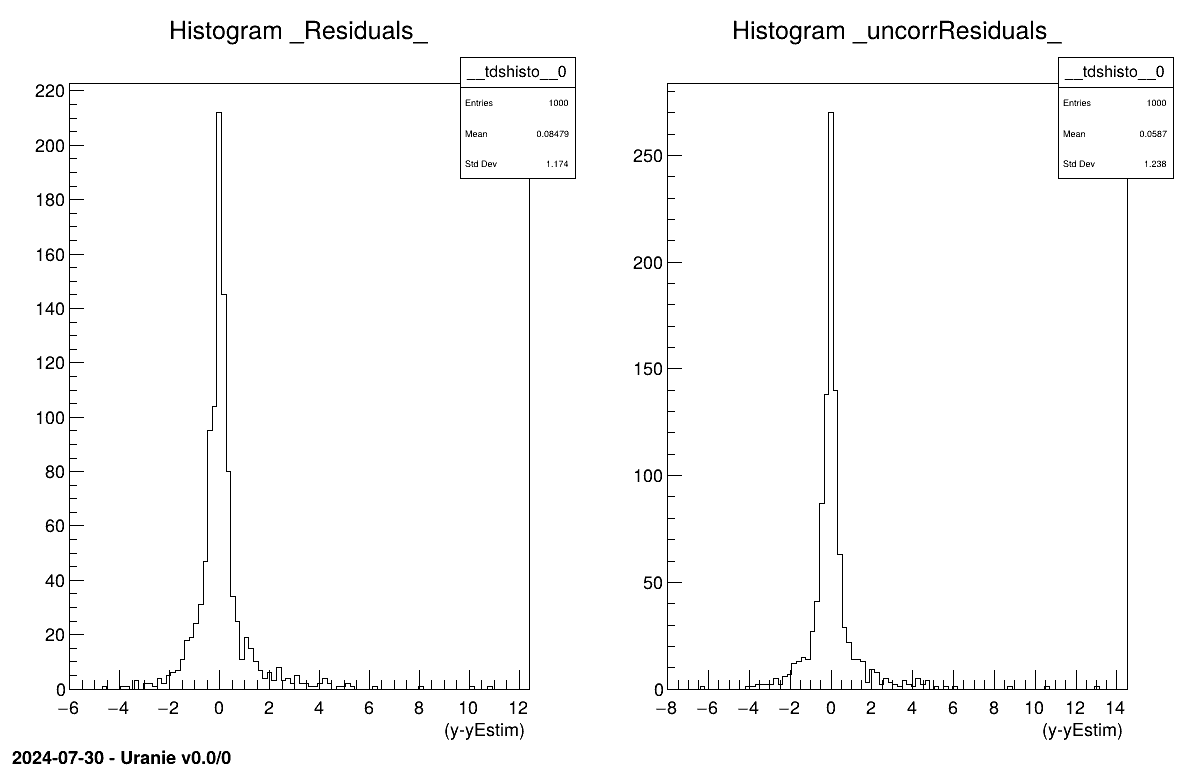It is not currently possible to export a kriging model as a standalone C or fortran function. There are various
reasons for this. The main one is that saving a kriging model means saving several matrices which can be huge when the
number of observations and/or the number of input variables is large. It is thus impractical to save them in a text
format as is usually done for the other algorithms of URANIE::Modeler.
The alternative is to export the information needed to build the
TKriging object with a TGPBuilder. This is done by the function
exportGPData:
gpb.findOptimalParameters("ML", 100, "neldermead", 500)
# export optimal parameters to a file
gpb.exportGPData("modelData.dat")The file created ("modelData.dat") is a standard "Salome table" file, with a special
#TITLE line in its header:
#NAME: tdsKriging #TITLE: URANIE::Modeler::TMatern32CorrFunction: [1.61744349e+00 1.43718257e+00 1.50122179e+00 6.79556828e+00]; variance: 7.09060005e+01; #DATE: Wed Aug 6 10:24:36 2014 #COLUMN_NAMES: x1| x2| x3| x4| y| tdsKriging__n__iter__ 2.186488000e-01 1.534173000e-01 6.196718000e-01 3.452344000e-01 1.235132000e+00 1 9.467816000e-02 3.830201000e-01 5.978722000e-03 7.689013000e-01 2.527613000e+00 2 4.716125000e-01 1.566920000e-01 8.623332000e-01 9.878017000e-01 -6.464496000e-01 3 1.346335000e-01 7.979628000e-02 5.091562000e-01 7.396531000e-01 2.461238000e+00 4 6.238671000e-01 2.995599000e-01 2.385627000e-01 9.548934000e-01 -3.266630000e-03 5 ...
The #TITLE line contains the class name of the correlation function, its parameters, the
variance of the gaussian process, and any other parameter required to construct the kriging model. The rest of the file
contains the observation inputs and output.
Warning
Do not modify the content of the file unless you know exactly what you are doing. It may produce a model which has nothing to do with the original one, or the file may not be readable at all.
The script below presents how to reconstruct the model from the saved file:
"""
Example of Gaussian Process loading
"""
from rootlogon import DataServer, Modeler
# Load the model data file into a data server
# VERY IMPORTANT: do not give any name or title to this tds !
tdsModelData = DataServer.TDataServer()
tdsModelData.fileDataRead("modelData.dat")
# Create a GP builder based on this data server
gpb = Modeler.TGPBuilder(tdsModelData)
# Create the kriging model
krig = gpb.buildGP()
# Display model information
krig.printLog()
The constructor of the TGPBuilder object takes only the dataserver with the model
data. It reads the #TITLE line and extracts the information. It is thus not necessary to call
findOptimalParameters. The function buildGP can be used immediately to
create the model. This macro is finished by printing the resulting model:
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
9.7238e-01 (9.7183e-01 )
8.5615e-01 (8.5606e-01 )
9.4116e-01 (9.4013e-01 )
4.3909e+00 (4.3948e+00 )
Variance of the gaussian process: 18.1787
RMSE (by Leave One Out): 0.510406
Q2: 0.842968
*******************************
The function TGPBuilder::findOptimalParameters greatly simplifies the process of finding
good parameters for the correlation function. However, in some cases, it might be interesting to perform this procedure
differently. In the following sections, we go "inside the engine" to allow advanced users to go beyond
findOptimalParameters if they want to.
A TGPBuilder object contains a TCorrelationFunction object which
will compute the correlation between the observation points. A clone of this correlation function object is stored in
the TKriging object, where it will estimate the correlation between the observations and a new
point.
It is possible to set the correlation function object manually, either at construction, or later using
TGPBuilder::setCorrFunction. Whether the user creates a new object or simply passes a keyword
to the TGPBuilder, a new correlation function object will be created inside the
TGPBuilder and destroyed with it.
The example below illustrates the construction of a TGPBuilder by passing a correlation
function object:
...
import numpy as np
# Definition of the initial correlation lengths
corrLengths = np.array([1.0, 0.25, 0.01, 0.3])
# Construction of the correlation function
corrFunc = Modeler.TMatern32CorrFunction(4, corrLengths)
# Construction of the GP builder
gpb = Modeler.TGPBuilder(tdsObs, "x1:x2:x3:x4", "y", corrFunc)
... The table below presents the list of correlation functions currently available in Uranie:
Table V.6. Correlation functions
| Class Name | keyword | number of parameters[a] | order of the parameters in the parameters array [b] |
|---|---|---|---|
| TExponentialCorrFunction | exponential | 2*d | [ p1, p2, ..., pd, l1, l2,..., ld ] |
| TGaussianCorrFunction | gauss | d | [ l1, l2,..., ld ] |
| TIsotropicGaussianCorrFunction | isogauss | 1 | [ l ] |
| TMaternICorrFunction | maternI | 2*d | [ v1, v2, ..., vd, l1, l2,..., ld ] |
| TMaternIICorrFunction | maternII | d+1 | [ v, l1, l2,..., ld ] |
| TMaternIIICorrFunction | maternIII | d+1 | [ v, l1, l2,..., ld ] |
| TMatern12CorrFunction | matern1/2 | d | [ l1, l2,..., ld ] |
| TMatern32CorrFunction | matern3/2 | d | [ l1, l2,..., ld ] |
| TMatern52CorrFunction | matern5/2 | d | [ l1, l2,..., ld ] |
| TMatern72CorrFunction | matern7/2 | d | [ l1, l2,..., ld ] |
[a] d is the number of dimensions of the input space [b] p is the power of the exponential; v is the regularisation parameter of the Matèrn function; l is the correlation length. | |||
For a more complete description of the available correlation functions (at least a more mathematical one) please report to [metho].
As mentioned before, Uranie provides three criteria (or cost functions) to select "good"
hyper-parameters for the kriging model. If needed, the user can create his own TGPCostFunction
object and apply his own searching method to find the optimal hyper-parameters.
The TGPCostFunction classes inherit from TSimpleEval and can thus
be used by a TMaster (cf. Chapter VIII). Complete examples
of how to use a cost function object are given in the next sections.
The example below illustrate the "manual" search for optimal hyper-parameters through a screening of the parameters space.
"""
Example of GP model estimation by LHS estimation
"""
import numpy as np
from rootlogon import DataServer, Modeler, Relauncher, Sampler
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construct the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, "x1:x2:x3:x4", "y", "matern3/2")
# construction of the cost function
cost = Modeler.TGPMLCostFunction(gpb)
# ---------------------------------#
# Construction of the LHS sampling #
# ---------------------------------#
# construction of the attributes
cl1 = DataServer.TLogUniformDistribution("cl1", 1e-6, 10.0)
cl2 = DataServer.TLogUniformDistribution("cl2", 1e-6, 10.0)
cl3 = DataServer.TLogUniformDistribution("cl3", 1e-6, 10.0)
cl4 = DataServer.TLogUniformDistribution("cl4", 1e-6, 10.0)
# Construction of the data server containing the exploration
# of the correlation lengths' space
tdsParam = DataServer.TDataServer("tdsParam", "")
tdsParam.addAttribute(cl1)
tdsParam.addAttribute(cl2)
tdsParam.addAttribute(cl3)
tdsParam.addAttribute(cl4)
# Construction of the sampler and generation of the data
screeningSize = 1000
s = Sampler.TBasicSampling(tdsParam, "lhs", screeningSize)
s.generateSample()
# Evaluate the cost function on the sampling
laun = Relauncher.TLauncher2(tdsParam, cost, "cl1:cl2:cl3:cl4", "cost:varGP")
laun.solverLoop()
# ----------------------------------------------------------#
# Search for the minimum value of the cost and retrieve the #
# corresponding correlation lengths #
# ----------------------------------------------------------#
# Retrieve the cost values
costValues = tdsParam.getTuple().getBranchData("cost")
Values = [costValues[i] for i in range(screeningSize)]
# find the index of the minimum cost
optimalCost = min(Values)
minIndex = Values.index(optimalCost)
# retrieve the values of the optimal correlation lengths
optimalParams = np.array([0., 0., 0., 0.])
optimalParams[0] = tdsParam.getValue("cl1", minIndex)
optimalParams[1] = tdsParam.getValue("cl2", minIndex)
optimalParams[2] = tdsParam.getValue("cl3", minIndex)
optimalParams[3] = tdsParam.getValue("cl4", minIndex)
# retrieve the value of the GP variance
optimalVar = tdsParam.getValue("varGP", minIndex)
# ----------------------------------------------------------#
# Update the GP Builder with the newly found parameters and #
# create the model #
# ----------------------------------------------------------#
# set the parameters of the correlation function
gpb.getCorrFunction().setParameters(optimalParams)
# set the GP variance
gpb.setVariance(optimalVar)
# Create the model
krig = gpb.buildGP()
# Display model information
krig.printLog()
The first step of the procedure is similar to what we have seen so far: we are loading the observations into a data
server and create a TGPBuilder. The change occurs when we create a TGPMLCostFunction
object. It will allow us to evaluate the likelihood of the gaussian process for a given set of hyper-parameters. For
this, it needs an access to the observations, the correlation function, etc. This is done by giving it a pointer to
the TGPBuilder object.
The next step is to create the dataset which will allow us to explore the parameter space. In this example, we only
care about the correlation lengths along each of the 4 input variables. We create a
TLogUniformDistribution object for each of them in order to have a good screening resolution
on small correlation lengths. Then, we create the dataserver that will hold the dataset, add the attributes to it,
create a sampler object and generate the data (cf. Chapter III for
details).
When the dataset is ready, we need to evaluate the cost function on it. An easy way to do it is to create a
TLauncher2 object, and give it the dataset, the cost function object, the input names, and the
output names. When the function solverLoop is called, the entries of the dataset are sent to
the cost function, and the results of the latter are stored in the dataserver.
The next operation is the retrieval of the optimal parameters. We need to identify the point with the minimal cost,
and extract the values of the corresponding correlation lengths and GP variance. When done, we need to manually
update the TGPBuilder. First, we set the new parameters of the correlation function by retrieving the correlation
function pointer (using TGPBuilder::getCorrFunction), and by calling
TCorrelationFunction::setParameters. Then, we set the variance of the gaussian process by
calling TGPBuilder::setVariance.
At this stage, the TGPBuilder object is ready to create a kriging model with the new hyper-parameters found. This is
what we do by calling buildGP.
This example is a simplified version of what is done inside findOptimalParameters. But here,
we can decide to distribute the computations, use another screening procedure, etc. We can even use another cost
function !
The resulting model is printed as follow:
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
4.4685e-01 (4.4660e-01 )
2.3956e-01 (2.3953e-01 )
2.9826e-01 (2.9794e-01 )
1.6450e+00 (1.6464e+00 )
Variance of the gaussian process: 1.89625
RMSE (by Leave One Out): 0.578768
Q2: 0.798086
*******************************
The example below illustrate the "manual" search for optimal hyper-parameters through a direct optimisation.
"""
Example of GP estimation by optimisation
"""
import numpy as np
from rootlogon import DataServer, Modeler, Reoptimizer
# Load observations
tdsObs = DataServer.TDataServer("tdsObs", "")
tdsObs.fileDataRead("utf_4D_train.dat")
# Construction of the GPBuilder
gpb = Modeler.TGPBuilder(tdsObs, "x1:x2:x3:x4", "y", "matern3/2")
# Construction of the cost function
costFunc = Modeler.TGPMLCostFunction(gpb)
# -------------------------------------------#
# Construction of the parameters to optimise #
# -------------------------------------------#
# construction of the input attributes
cl1 = DataServer.TAttribute("cl1", 1e-6, 10.0)
cl2 = DataServer.TAttribute("cl2", 1e-6, 10.0)
cl3 = DataServer.TAttribute("cl3", 1e-6, 10.0)
cl4 = DataServer.TAttribute("cl4", 1e-6, 10.0)
# construction of the output attributes
cost = DataServer.TAttribute("cost")
varGP = DataServer.TAttribute("varGP")
# Construction of the data server containing the parameters to optimise
tdsParam = DataServer.TDataServer("tdsParam", "")
tdsParam.addAttribute(cl1)
tdsParam.addAttribute(cl2)
tdsParam.addAttribute(cl3)
tdsParam.addAttribute(cl4)
# Add the parameters to optimise to the cost function
costFunc.addInput(cl1)
costFunc.addInput(cl2)
costFunc.addInput(cl3)
costFunc.addInput(cl4)
costFunc.addOutput(cost)
costFunc.addOutput(varGP)
# ------------------------------#
# Construction of the optimiser #
# ------------------------------#
# Choice of an optimisation algorithm
solver = Reoptimizer.TNloptNelderMead()
# Construction of the optimizer, which receives the data server storing
# the optimal result, the criterion and the optimisation algorithm.
opt = Reoptimizer.TNlopt(tdsParam, costFunc, solver)
# Optimisation options
opt.addObjective(cost) # criterion to minimise
start = np.array([1e-2, 1e-2, 1e-2, 1e-2])
opt.setStartingPoint(len(start), start) # starting point for the optimisation
opt.setMaximumEval(1000) # maximum number of evaluation calls
opt.setTolerance(1e-12) # convergence criterion
# Launch the optimisation procedure
opt.solverLoop()
# ----------------------------------------------------------#
# Update the GP Builder with the newly found parameters and #
# create the model #
# ----------------------------------------------------------#
# Retrieve the optimal parameters. In this case, the data server contains only
# one set of parameters, thus we don't have to search for the minimal cost.
optimalParams = np.array([0., 0., 0., 0.])
optimalParams[0] = tdsParam.getValue("cl1", 0)
optimalParams[1] = tdsParam.getValue("cl2", 0)
optimalParams[2] = tdsParam.getValue("cl3", 0)
optimalParams[3] = tdsParam.getValue("cl4", 0)
# set the parameters of the correlation function
gpb.getCorrFunction().setParameters(optimalParams)
# Retrieve the computed variance
optimalVar = tdsParam.getValue("varGP", 0)
# Set the new variance of the GP
gpb.setVariance(optimalVar)
# Create the model
krig = gpb.buildGP()
# Display model information
krig.printLog()
The beginning of the script is the same as in the previous example (see Section V.6.4.3). The first difference concerns the construction of the
attributes representing the parameters to optimise. Here, we do not need to define a distribution for the variables:
we just need boundaries. This is the reason why all the input attributes are TAttribute
objects, with a minimum and maximum value. The output attributes have no predefined boundaries.
After defining the input and output attributes, we need to create a dataserver to store the results of the optimisation. We provide it only with the input attributes. The output attributes will be automatically added during the optimisation procedure. We also need to tell the cost function which attributes represent the parameters to optimise, and which attributes represents the outputs of the cost function.
The next step is the construction of the optimiser. As explained in Chapter IX, an
optimiser needs three objects to perform an optimisation procedure: a dataserver to store the results, a cost
function to evaluate the criterion (or the criteria, for multi-objectives optimisation), and an optimisation
algorithm to propose a new set of input parameters. The two former objects are already created. In our example, the
latter is a TNloptNelderMead object.
Once constructed, the optimiser object must receive some additional information before starting the procedure. The
first one are the output attributes of the cost function corresponding which correspond to the criteria. In this
example, we have only one criterion: the attribute "cost" which refers to the negative log-likelihood of the gaussian
process. The second mandatory information is the starting point of the optimisation. More than one starting point can
be provided. As many optimal set of parameters will be stored in the dataserver. Finally, non mandatory options can
be set, like the maximum number of evaluations of the cost function, or the tolerance criterion used to consider that
the optimisation has converged to a solution. When everything is set, we can launch the optimisation procedure by
calling the solverLoop function.
Retrieving the optimal parameters is easier in this case than in the LHS: only the optimal solutions for each
starting point are stored in the dataserver ! As we have only one starting point in this example, we have only one
solution to extract and provide to the TGPBuilder. Once done, we can create our kriging model as we did before.
The resulting model is printed as follow:
*******************************
** TKriging::printLog[]
*******************************
Input Variables: x1:x2:x3:x4
Output Variable: y
Deterministic trend:
Correlation function: URANIE::Modeler::TMatern32CorrFunction
Correlation length: normalised (not normalised)
1.6180e+00 (1.6171e+00 )
1.4371e+00 (1.4369e+00 )
1.5025e+00 (1.5009e+00 )
6.7885e+00 (6.7944e+00 )
Variance of the gaussian process: 70.8649
RMSE (by Leave One Out): 0.49911
Q2: 0.849841
*******************************
| |  | |
| V.5. The artificial neural network |  | Chapter VI. The Sensitivity module |