English Français

Documentation / User's manual in Python : PDF version

Chapter VI. The Sensitivity module
Chapter VI. The Sensitivity module
Prev   Next

Chapter VI. The Sensitivity module

Abstract

This part describes the Sensitivity module whose main goal is to estimate what proportion of variations in the output of the model each input parameter is responsible for.
The source files are stored in souRCE.git/meTIER/launCHER/souRCE and the corresponding namespace is URANIE::Sensitivity.

Table of Contents

VI.1. Brief reminder of theoretical aspects
VI.1.1. Content of the TSensitivity class
VI.1.2. List of available methods
VI.2. The finite differences method
VI.2.1. General presentation of finite difference sensitivity indices
VI.2.2. Computation of local sensitivity indices with the finite differences method
VI.3. The regression method
VI.3.1. General presentation of regression's coefficients
VI.3.2. Computation of the coefficients with Uranie
VI.4. The Morris screening method
VI.4.1. Principle of the Morris' method
VI.4.2. The Morris' method in Uranie
VI.5. The Sobol method
VI.5.1. Introduction to Sobol's sensitivity indices
VI.5.2. Computation of Sobol's sensitivity indices
VI.6. Fourier-based methods
VI.6.1. Introducing the method
VI.6.2. Implementation of methods
VI.6.3. Computation of Sobol indices with the FAST method
VI.6.4. Computation of Sobol indices with the method RBD
VI.7. The Johnson relative weight
VI.7.1. General overview
VI.8. Sensitivity Indices based on HSIC
VI.8.1. Introduction to sensitivity measures using HSIC

VI.1. Brief reminder of theoretical aspects

In this section, we will briefly remind the different ways to measure the sensitivity of an output to the inputs of the model. A theoretical introduction is given in [metho] to help handle the concept discussed throughout the examples below.
The list of methods available in Uranie will also be briefly discussed, as most of these procedures, local and global ones, are further discussed in the following sections (both implementation and cost in terms of number of assessments).

VI.1.1. Content of the TSensitivity class

As for the mathematical function discussed in Section V.3.1.1, the sensitivity classes are now able to cope with constant-size vectors, considering every elements with respect to their counterpart in the other events (leading also to a removal of the previous limitation on the possible number of output attribute to be studied). Most of these classes are based on the TSensitivity one, which mainly contains:

  • Pointers:

    • to a TDataServer object

    • to TCode object, and to a TMethodCall object (to deal respectively with external code and ROOT-interactive function)

    • to a TRandom object (ROOT-class for random drawing)

    • to a TDSNtupleD object and to a TTree that contains all the results

    • to two TList of input and output attributes.

  • Methods:

    • computeIndexes: This is the main method for the evaluation. It checks whether the TDSNtupleD is existing (if not, it creates it) and filled with inputs and outputs (if not, it launches either the code or function). There are few possible options common to all the classes that inherit from the TSensitivity one:

      • "noIntermediateSaved": This is useful if the code to be launched is quick, to prevent from having every event written to a physical file on disk (it waits the very end of the process to do so, as stated in Section IV.3).

      • "output=": This option reduce the number of output to be considered for the sensitivity analysis. The requested pattern following the equal sign is a usual string where ":" is used as delimiter between two fields. This option is further discussed, considering the constant-size vector case, in the tip box below.

      With all this, it calls the evaluateIndexes method (providing the same options).

    • evaluateIndexes: Method (empty in TSensitivity) in which indices estimation will be done specifically by inheriting-classes. Should not be called by users or with good reasons (discussed with developpers).

    • fillIndex: Never redefined, this method fills the results TTree with the method, algorithm, input attribute and value of the sensitivity index (along with its upper and lower 95% confidence interval boundaries).

    • drawIndexes: Draw the measured indices. This method takes three arguments, the first one being the title, the second one a selection cut and the last one the options. The latter parameter is composed of different key words separated by commas. These key words can be:

      • nonewcanv: if not present, a new canvas is made, else it is up to the user to provide one. The difference mostly lies in the memory management and in the way the display is done (if one wants to have multi-pad canvas for instance).

      • pie/hist: whether the resulting plot should be displayed as pie or chart.

      • total/first: to decide which index should be shown (see [metho] for more explanations on this aspect).

      As this method is generic for all classes that inherit from the TSensitivity one, it will always provide a pie chart with the first indices on the left and another one with the total indices on the right, when the "pie" options is passed, disregarding whether the method under consideration can estimate both kind of index. If it is not the case, the right panel will be a copy of the left one. In this method, the second argument might be in particular use when dealing with more than one output: the drawIndexes method assumes that the requested output to be drawn is the first output defined and estimated through your sensitivity analysis. In the case wher several outputs were investigated, the selection field might be used as done below to specified that tutu is the output in which one is interested in: 

      tsobol.drawIndexes("What a nice plot", "Out==\"tutu\"", "all,hist,nonewcanv")

Tip

All sensitivity classes can deal with vectorial outputs, provided that they are constant-size one. All methods are transparent and it is also possible to restrain the sensitivity analysis to some specific elements of vector. Let's consider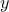 , the output of the code. One can investigate the first, tenth and fifteenth elements by either:

  • using the "output=" option (here "output=y[0]:y[10];y[15]"), either passed at the construction or when calling the computeIndexes method.

  • specifying in a constructor that requested the const char* out field, the following list "y[0]:y[10];y[15]", instead of "y".

If both methods are chosen with different elements, the results will be the estimation for all the elements requested.

Tip

All sensitivity have been modified for Uranie version greater than 4.1 in order to be able to cope with the Relauncher architecture. A new constructor has been created requesting a pointer to a TRun object which has to be chosen amongst the three following types:

  • TSequentialRun

  • TThreadedRun

  • TMpiRun

This object will contain all the information about the way to handle evaluators, whether they are

  • C++ function

  • Python function

  • External Code

  • Any composition of instances of previously introduced evaluators

For a more general discussion on these aspects, see Section VIII.2.

With this set, one can look at the different methods listed below.

VI.1.2. List of available methods

Methods for Sensitivity Analysis (SA) are split into two types:

  • local: variations around a nominal value,
  • global: variations in all the domain.

Currently, one local method and six global methods are implemented for Sensitivity Analysis. All of them have been recently adapted in order to be able to cope with constant-size vector case, considering, as for the statistic, that every element can be considered independent from the other one. This leads to the fact that now, every methods can deal with more than one output as well. The list below provides a concise description of each and every implemented methods. For a more refined theoretical description, please, see [metho].

  1. Finite differences (local method):

    It consists in estimating the partial derivatives around a nominal value for each input parameters (see Section VI.2).

  2. Values Regression method (linearity):

    It performs a sensitivity analysis based on the coefficients of a normalised linear regression (see Section VI.3).

  3. Ranks Regression method (monotony):

    Here, the analysis is based on the coefficients of a normalised rank regression (see Section VI.3).

  4. Morris' screening method:

    It consists in ordering the input variables according to their influence on the output variables. This method should be used for input ranking. Despite the low computational cost encountered, the obtained information is insufficient to get a proper quantitave estimation of the impact of the input variable on the output under consideration (see Section VI.4).

  5. Sobol method:

    This method produces numerical values for the Sobol indices. However, it requires a high numerical cost as numerous code assessments are needed (see Section VI.5).

    It is based on the so-called Saltelli & Tarontola method, to compute the first and total order indices, using different algorithms.

  6. FAST method:

    It computes Sobol's first order indices from Fourier coefficients, using a sample on a periodic curve with different frequencies for each input variables (see Section VI.6).

  7. RBD method:

    It computes Sobol's first order indices from Fourier coefficients, using a sample on a periodic curve with an unique frequency (see Section VI.6).

  8. Johnson's relative weights method:

    It computes the relative weights which are aimed to be a good approximation of the Shapley's values, but whose main advantage is to be a lot quicker to estimate. This method is limited to linear cases (see Section VI.7).

Warning

If the FAST or RBD methods are to be used, then the FFTW library must be installed firstly (and ROOT must have linked installed once FFTW is installed).

All the methods will be applied on the flowrate function, introduced in Section IV.1.2.

Prev   Next
V.6. The kriging method Home VI.2. The finite differences method
/language/en