English Français

Documentation / User's manual in Python : PDF version

VI.3. The regression method
VI.3. The regression method
Prev Chapter VI. The Sensitivity module Next

VI.3. The regression method

VI.3.1. General presentation of regression's coefficients

The TRegression class is dealing with computing the SRC and SRRC coefficients but also the PCC and PRCC ones (for a definition of these coefficients, see [metho]). The choice of which values to be computed between these four is set at the construction by precising respectively "src", "srrc", "pcc" or "prcc" and is no more inclusive. It is indeed now possible to get, for example, the results of both SRC and PRCC estimation by passing the option "srcprcc", for one or more outputs. This class computes the regression coefficients from the observations of the model contained in a TDataServer. The construction of the data sample is the user burden and the quality of the regression coefficients computed will depend upon it (unless analysing a dataset out of an experiment).

In the case where SRC or SRRC coefficients are requested, a second estimation is performed, based on correlation coefficients (between the output and the input under consideration, see [metho] for completness). This estimation is costless and allows to get an idea of the 95% confidence-interval (CI) of the estimated coefficient. This CI has to be considered as a very good guess of the 95% CI and could only be considered exact, if one respects the underlying hypothesis for its estimation: all input variables should be gaussian-distributed variables. An illustration of the way to look at this CI is shown in Section VI.3.2.5.1.

Using the TRegression class is simple, as there is only one possible creator, and the only other method to be called is computeIndexes. The rest is common to any of the following SA classes.

VI.3.2. Computation of the coefficients with Uranie

Computing Standardised Regression Coefficients (SRC), Standardised Rank-Regression Coefficients (SRRC), partial correlation coefficient (PCC) and partial rank correlation coefficient (PRCC) in Uranie is dealt with the TRegression class which inherits from the TSensitivity class. The following sections will explain how to compute and handle the requested coefficients.

VI.3.2.1. Example: simple computation of SRC and SRRC coefficients

The example script uses the TRegression class to compute and display the SRC and SRRC coefficients: 

"""
Example of SRC and SRRC estimation
"""
from rootlogon import ROOT, DataServer, Sensitivity

# Define the DataServer and fill it with datas in a file
tds = DataServer.TDataServer("tdsflowrate", "DataBase flowrate")
tds.fileDataRead("sampleLHSFlowrateModel4000points.dat")

# Create a TRegression object and compute indexes
treg = Sensitivity.TRegression(tds, "rw:r:tu:tl:hu:hl:l:kw",
                               "flowrateModel", "SRCSRRC")
treg.computeIndexes()

# Draw SRC Indexes
cc = ROOT.TCanvas("canpie-SRC", "Pie chart SRC", 10, 32, 1200, 800)
apad = ROOT.TPad("apad", "apad", 0, 0.03, 1, 1)
apad.Draw()
apad.cd()
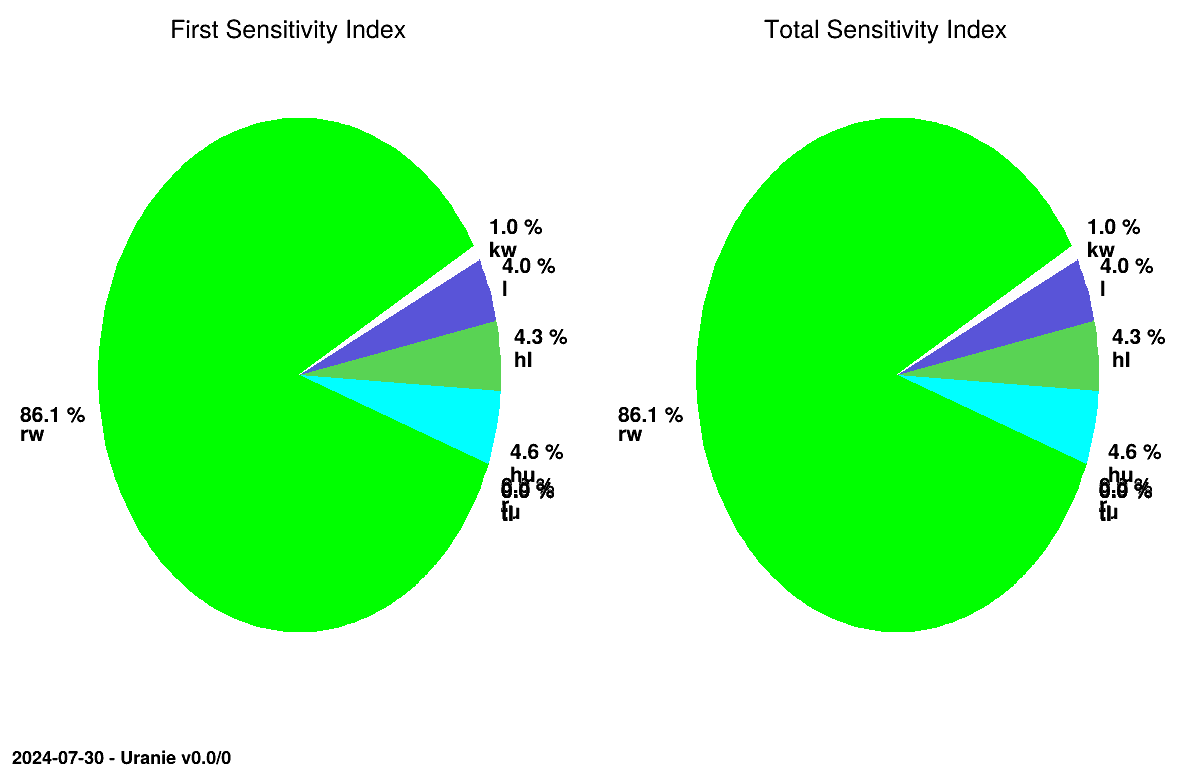
treg.drawIndexes("Flowrate", "", "nonewcanv, pie, SRC")

# Draw SRRC Indexes
ccc = ROOT.TCanvas("canpie-SRRC", "Pie chart SRRC", 10, 32, 1200, 800)
pad2 = ROOT.TPad("pad2", "pad2", 0, 0.03, 1, 1)
pad2.Draw()
pad2.cd()
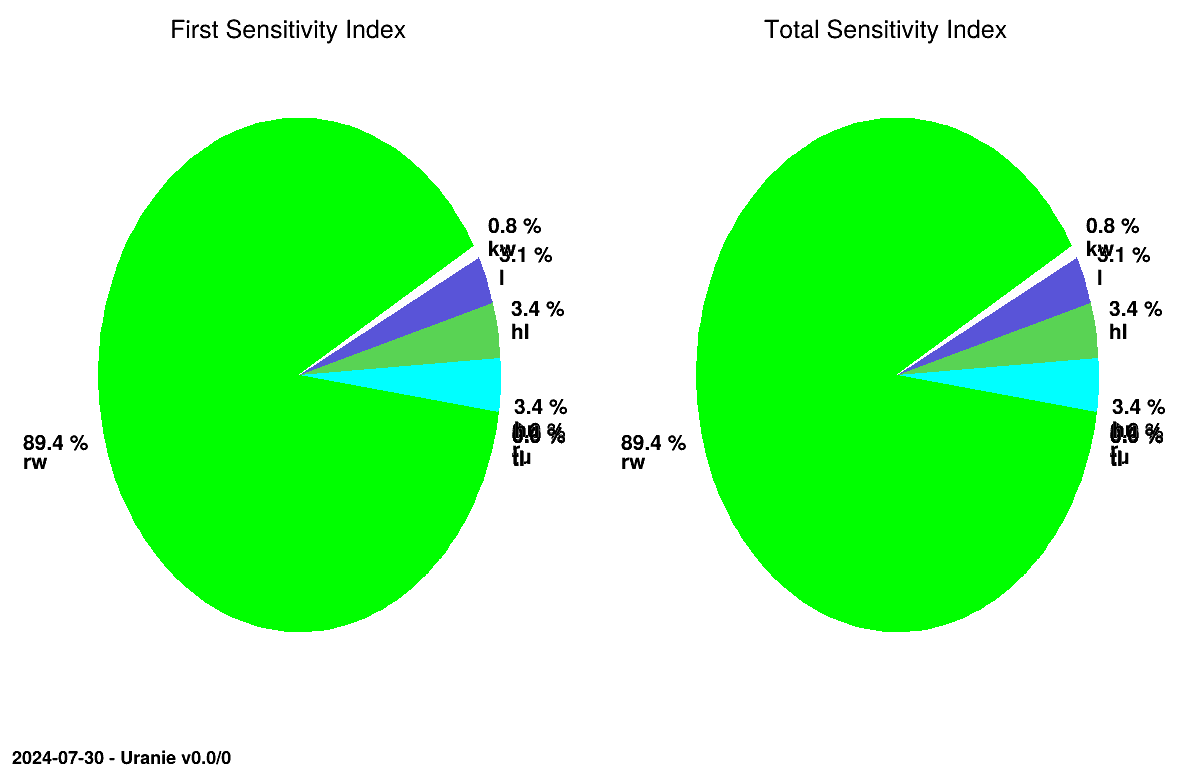
treg.drawIndexes("Flowrate", "", "nonewcanv,pie,SRRC")

In this script, the observations are data loaded from a file into a TDataServer object, a TRegression object is created to compute the coefficients. Then both indices are computed by using the method TSensitivity::computeIndexes. Finally, SRC and SRRC coefficients are graphically displayed in pie charts, respectively in Figure VI.1 and Figure VI.2, with the TSensitivity::drawIndexes method.

Figure VI.1. SRC coefficients estimated for the flowrate function.

SRC coefficients estimated for the flowrate function.

Figure VI.2. SRRC coefficients estimated for the flowrate function.

SRRC coefficients estimated for the flowrate function.

VI.3.2.2. TRegression constructor

To build a TRegression object, use the following constructor: 

TRegression(tds, varinput, varoutput, option = "src")

The TRegression constructor needs:

  • a pointer to a TDataServer object where the input and output attributes are stored,
  • a string containing the input parameter names separated by colons (ex. "rw:r:tu:tl:hu:hl:l:kw"),
  • a string containing the name of the model's outputs (ex. "flowrateModel"),
  • a string containing the type of coefficient to compute ("SRC", "SRRC", "PCC", or "PRCC"), its default value is the string "SRC".

The creation of a TRegression object for computing the SRC and the SRRC coefficients is therefore: 

# Create a TRegression object and compute SRC indices
treg = Sensitivity.TRegression(tds, "rw:r:tu:tl:hu:hl:l:kw", "flowrateModel", "SRCSRRC")

VI.3.2.3.  Computing the SRC and SRRC indices

The computation of the coefficients (also call indices) is done with the method computeIndexes: 

computeIndexes(option)

In our example, its use is therefore: 

# Compute the indices
treg.computeIndexes()

VI.3.2.4. Displaying the indices

To display graphically the coefficients, use the drawIndexes method: 

drawIndexes(sTitre, select, option)

The method needs:

  • a TString containing the title of the figure,
  • a string containing a selection (empty if no selection),
  • a string containing the options of the graphics separated by commas.

Some of the options available are:

  • "nonewcanv": to not create a new canvas,
  • "pie": to display a pie chart,
  • "hist": to display a histogram,
  • "SRC": to display the SRC indices,
  • "SRRC": to display the SRRC indices,
  • "PCC": to display the PCC indices,
  • "PRCC": to display the PRCC indices,

In our example the use of this method is: 

# Draw SRC Indices
cc = ROOT.TCanvas("canpie-SRC", "Pie chart SRC")
treg.drawIndexes("Flowrate", "", "nonewcanv,pie,SRC")

# Draw SRRC Indices
ccc = ROOT.TCanvas("canpie-SRRC", "Pie chart SRRC")
treg.drawIndexes("Flowrate", "", "nonewcanv,pie,SRRC")

Here is another example with a histogram figure:

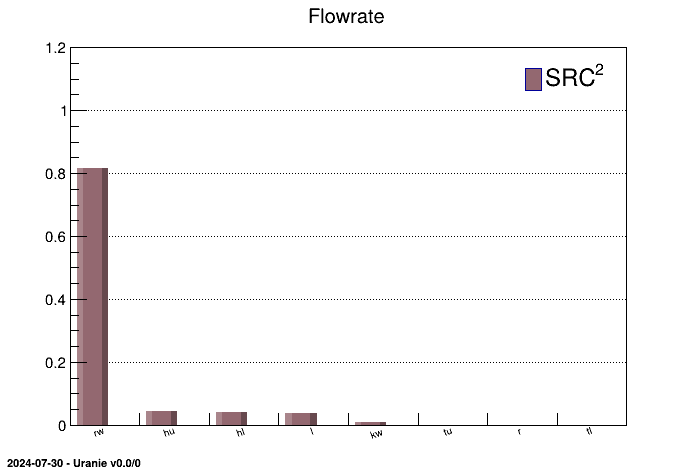
cccc = ROOT.TCanvas("canhist-SRC", "Hist chart SRC")
treg.drawIndexes("Flowrate", "", "nonewcanv,hist,first")

Figure VI.3. Histogram of SRC coefficients

Histogram of SRC coefficients

VI.3.2.5. Extracting the coefficients

The coefficients, once computed, are stored in a TTree. To get this TTree, use the method TSensitivity::getResultTuple(): 

results = treg.getResultTuple()

Several methods exist in ROOT to extract data from a TTree, it is advised to look for them into the ROOT documentation. We propose two ways of extracting the value of each coefficient from the TTree.

VI.3.2.5.1. First method of extraction

The first method use the method getValue of the TRegression object specifying the order of the extract value, the related input and possibly more selected options. 

Rw_Indexe = treg.getValue("First","hl");
VI.3.2.5.2. Second method of extraction

The second method uses 3 steps to extract an index:

  • scan the TTree for the chosen input variable (with a selection) in order to obtain its row number. In our example, if we chose the variable "hl", we'll use the command: 
    results.Scan("*", "((Inp==\"hl\")&&(Method==\"SRC^2\"))")
    This results in the following table, in which the SRC coefficient of "hl" is in the row 40: 
    **************************************************************************************
*    Row   *   Out *  Inp * Order * Method *      Algo *   Value * CILower * CIUpper *
**************************************************************************************
*       40 * flowr *   hl * First *  SRC^2 * --first-- * 0.04102 *      -1 *      -1 *
*       41 * flowr *   hl * Total *  SRC^2 * --total-- * 0.04102 *      -1 *      -1 *
*       42 * flowr *   hl * First *  SRC^2 * --rho^2-- * 0.04124 * 0.03025 * 0.05353 *
*       43 * flowr *   hl * Total *  SRC^2 * --rho^2-- * 0.04124 * 0.03025 * 0.05353 *
**************************************************************************************
    The numbers stored in row 42 are the estimation using the correlation coefficient between the output and the input under consideration, and they are shown to crosscheck the main estimation and to display the estimated 95% confidence interval (CI), see Section VI.3.1 and [metho] for more explanations.
  • set the entry of the TTree on this row with the method GetEntry;
  • get the value of the index with GetValue method on the "Value" leaf of the TTree.

Below is an example of extraction of the index for the variable "hl" in our flowrate case: 

results.Scan("*", "((Inp==\"hl\")&&(Method==\"SRC^2\"))")
results.GetEntry(20)
Rw_Indexe = results.GetLeaf("Value").GetValue()
VI.3.2.5.3. Third method of extraction

The second method uses 2 steps to extract an index:

  • use the Draw method with a selection to select the index, for example the selection for the SRC coefficient of "rw" is "Inp==\"rw\" && Algo==\"--first--\"";
  • get the pointer on the value of the index with the GetV1 method on the TTree.

Below is another example of extraction of the index for the variable "rw" in our flowrate case: 

results.Draw("Value", "Inp==\"rw\" && Algo==\"--first--\" && Method==\"SRC^2\" ", "goff")
Rw_Indexe = results.GetV1()[0]

VI.3.2.6. Getting and

To evaluate the pertinence of the indices, it is recommended to check the value of both 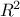and 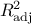. The use of the methods TRegression::getR2 and TRegression::getR2A is now deprecated: as one can work both on rank and values at the same time, the quality criteria can be computed for all the estimations and so they have to be kept in the ntuple result as well. The numerical values can then be retrieved as previously explained, an example is shown below to get the one from the regression on values (SRC).

Example:

# coefficient of determination R2
results.Draw("Value", "Inp==\"__R2__\" && Algo==\"--first--\" && Method==\"SRC^2\" ", "goff")
Rw_Indexe = results.GetV1()[0]

# adjusted coefficient of determination R2A
results.Draw("Value", "Inp==\"__R2A__\" && Algo==\"--first--\" && Method==\"SRC^2\" ", "goff")
Rw_Indexe = results.GetV1()[0]

VI.3.2.7. Getting the sum of squared indices

As stated in [metho], it can be interesting to consider the sum of the squared indices (in particular for SRC coefficients). As for the quality criteria, discussed previously, this computation can be done for all the estimations and so it has to be kept in the ntuple result. The numerical values can then be retrieved as previously explained, an example is shown below to get the ones from the regression on values (SRC).

Example:

# coefficient of determination sum
results.Draw("Value", "Inp==\"__sum__\" && Algo==\"--first--\" && Method==\"SRC^2\" ", "goff")
Rw_Indexe = results.GetV1()[0]

Summary: TRegression

  • TRegression(TDataServer *tds, const char* varinput, const char* varoutput, Option_t *option="src")

    • tds: a dataserver containing the attributes of the input and output variables and their associated data.
    • varinput: input attribute names separated by colons. They represent all the inputs of the problem. They must refer to existing attributes in the "tds".
    • varoutput: attribute names which represent the responses of the problem. it must refer to existing attributes in the "tds".
    • option: a string containing the type of regression coefficients to compute: "SRC", "SRRC"; "PCC" or "PRCC" (Default = "src").

  • void computeIndexes(Option_t *option=""): Compute regression coefficients.

    • option: no option has been implemented.

  • void drawIndexes(TString sTitre, const char* select="", Option_t *option=""): draw the coefficients.

    • sTitre: a string containing the title of the figure.
    • select: a string containing a solution.
    • option: a string containing the options of the graphics separated by commas.

  • TTree * getResultTuple(): Get the tree containing the indices.

Prev Up Next
VI.2. The finite differences method Home VI.4. The Morris screening method
/language/en