Documentation
/ User's manual in Python
: 
| Chapter XI. The Calibration module | ||
|---|---|---|
 |  | |
Table of Contents
This section presents different calibration methods that are provided to help get a correct estimation of the parameters of a model with respect to data (either from experiment or from simulation). The methods implemented in Uranie are going from the point estimation to more advanced Bayesian techniques and they mainly differ from the hypothesis that can be used. They're all gathered in the in the libCalibration module. The namespace of this library is URANIE::Calibration. Each and every technique discussed later-on is theoretically introduced in [metho] along with a general discussion on calibration and particularly on its statistical interpretation.
The data provided as
reference will be compared to model predictions, the model being a
mathematical function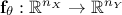 
. From now on and unless otherwise specified (for
distance definition for instance, see Section XI.1.1) the dimension of the output is
set to 1 (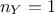
) which means
that the reference observations and the predictions of the model are scalars (the observation will then be written
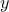and the prediction of the model
).
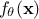On top of the input vector which
is problem-dependent, the model depends also on a parameter vector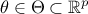 
which is constant but
unknown. The model is deterministic, meaning that 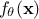is constant once both 
and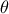 
are fixed. In the rest of this documentation, a given set of parameter value
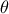is called a configuration.
The rest of this section introduces the distance between observations and the predictions of the model, in Section XI.1.1 while the methods are discussed in their own sections. The already predefined calibration methods proposed in the Uranie platform are listed below:
The minimisation, discussed in Section XI.3
The linear Bayesian estimation, discussed in Section XI.4
The ABC approaches, discussed in Section XI.5
The Markov-chain Monte-Carlo sampling, discussed in Section XI.6
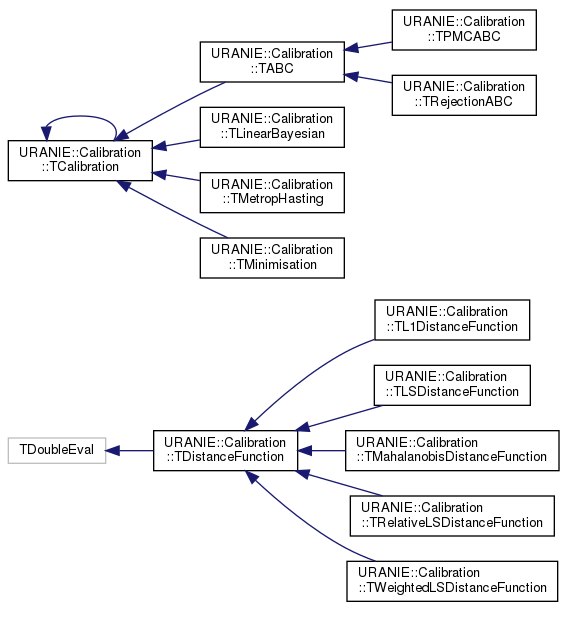
As for other modules, there is a specific class organisation that links the main classes in this module. The class
hierarchy is shown in Figure XI.1 and is discussed a bit here to explain the
the two main classes from which everything other classes are derived and corresponding shared function throughout the
method. One can see this organisation with the two sets of classes: those inheriting from the
TCalibration class and those inheriting from TDistanceFunction class. The
former are the different methods that have been developed to calibrate a model with respect to the observations and
each and every method will be discussed in the upcoming sections. Whatever the method under consideration, it always
includes a distance function object, which belongs to the latter category and its main job is to quantify how close the
model predictions are to the observations. These objects are discussed in the rest of this introduction, see for
instance in Section XI.1.1.
There are many ways to quantify the agreement of the observations (our references) with the predictions of the model
given a provided vector of parameter 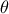. As a reminder, this step has to be run every time a new vector of parameter 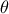is under investigation which means that the code
(or function) should be run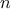 
times
for each new parameter vector.
Starting from the formalism introduced above, many different distance functions can be computed. Given the fact that
the number of variable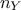 
used to
perform the calibration can be different than 1, one might also need variable weight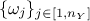 
that might
be used to ponderate the contribution of every variable with respect to the others. Given this, here is a
non-exhaustive list of distance functions:
L1 distance function (sometimes called Manhattan distance):
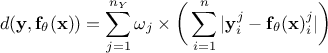
Least square distance function:
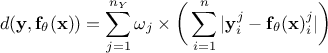
Relative least square distance function:
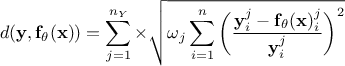
Weighted least square distance function:
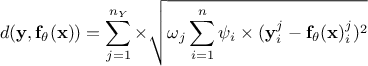where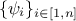 
are weights used to ponderate each
and every observations with respect to the others.
Mahalanobis distance function:
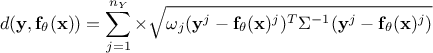where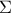 
is the covariance matrix of the observations.
Their implementation is discussed in Section XI.2.2
| | | |
| X.2. Efficient Global Optimization |  | XI.2. Calibration classes, distance functions, observations and model |