Documentation
/ Manuel utilisateur en Python
: 
This method is pretty simple from the algorithm point of view as it consists mainly in
the analytical formulation of the posterior distribution when the hypotheses on the prior are well set: the problem can
be considered linear and the prior distributions are normally distributed (or flat, as discussed in [metho]). Practically, handling this technique is done by following the recipe provided in Section XI.2 with an important difference though: the code or function, brought through the
constructor of the
Get the reference data, the model and its parameters. Choose the assessor type you'd like to use and construct the
Provide the input covariance matrix, i.e. the reference observation covariance (in [metho]
this would correspond to the
Provide the name of the regressors. This is also a key step as a regressor can be an input variable, but also any
function of one or many input variables, This is discussed in Section XI.4.2.
A transformation function can be provided but this is not compulsory. This is discussed in Section XI.4.3.
Finally the estimation is performed and the results can be extracted or draw with the usual plots. The
specificities are discussed in Section XI.4.3.
TLinearBayesian object, is not strictly speaking useful. The parameters
estimation is indeed analytical so the main point of providing an assessor is to get both the a
priori and a posteriori residue distributions. The important steps of this kind of
analysis are gathered here, all classical steps being gathered in the first item:
TLinearBayesian object accordingly with the suitable distance function. Even though this
mainly relies on common code, this part is introduced also in Section XI.4.1, in
particular for what happened to the distance function (pay attention to the warning bloc).
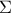 ). This is compulsory to get a valid estimation. This impact the distance function choice as
discussed in Section XI.4.2.
). This is compulsory to get a valid estimation. This impact the distance function choice as
discussed in Section XI.4.2.
The constructors that can be used to get an instance of the TLinearBayesian class are those
detailed in Section XI.2.3. As a reminder the prototype available are these ones:
# Constructor with a runner
TLinearBayesian(tds, runner, ns=1, option="")
# Constructor with a TCode
TLinearBayesian(tds, code, ns=1, option="")
# Constructor with a function using Launcher
TLinearBayesian(tds, fcn, varexpinput, varexpoutput, ns=1, option="")
The details about these constructor can be found in Section XI.2.3.1, Section XI.2.3.2 and Section XI.2.3.3
respectively for the TRun, TCode and
TLauncherFunction-based constructor. In all cases, the number of samples 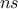 is set to 1 by default and changing it will
not change the results. As for the option, there are no specific options for this class.
is set to 1 by default and changing it will
not change the results. As for the option, there are no specific options for this class.
The final step here it to construct the TDistanceFunction which is the compulsory step which
should always come right after the constructor, but a word of caution about this step:
Warning
Whatever the distance function you're choosing, thesetDistanceAndReference is locally
redefined so that the distance function will only be a TMahalanobisDistance. As defining the
observation covariance matrix is mandatory, it would make little sense to use any other distance function which would
not use the full extend of the input information. Furthermore, the distance function, in this method, is only
provided for illustration purpose, to check the difference between the a priori and
a posteriori parameter's values.
Once the TLinearBayesian instance is created along with its
TDistanceFunction, two methods must be called before getting into the parameters
estimation. These methods are compulsory as they will define the heart of the analytical formula to get the Gaussian
parameter value of the a posteriori distribution (see [metho]).
The first one (even though there is no particular order between the two) is setRegressor,
whose prototype is
setRegressor(regressorname)
The only argument is the regressorname field, which is the list of regressor names split by ":", using
the usual format and this method, then, checks two things. The first one is the fact that the number of regressors
must match the number of parameters to be calibrated. On top of this, the code passes through the list of attributes
available in the reference observation TDataServer and check that every regressor name provided matches one existing
attributes. As stated above, if the observation TDataServer does not contains the regressors (when the input file is
loaded) these attributes have to be constructed from scratch either through TAttributeFormula
or by using another dedicated assessor (as done in the use-case shown in Section XIV.12.2).
The other method is setObservationCovarianceMatrix whose prototype is
setObservationCovarianceMatrix(mat)
The only argument here is a TMatrixD whose content is the covariance matrix of the reference
observation data. Once again, this method will check two things:
the provided matrix must have the correct number of rows and columns (basically both should be set to
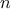 );
);
the provided matrix should be symmetrical;
Given this, estimations can be performed. One can find an example of how to use these methods in the use-case dedicated subsection, more precisely in Section XIV.12.2.
Finally once the computation is done there are three different kinds of results and several ways to interpret but also transform it. This section details some important and specific aspect to it.
The idea is that when you want to consider your model as linear, you might have to transform it a bit to have a
correct linear behaviour and to express and compute the needed regressors. For this peculiar behaviour, one will
rely on our use-case discussed in Section XIV.12.2. In this case, one should linearise the flowrate
function as done here by writing:
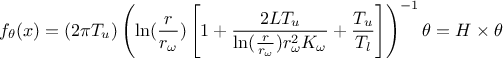
where the regressor can be expressed as
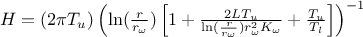 . From there, it is clear that we will be calibrating a newly
defined parameter
. From there, it is clear that we will be calibrating a newly
defined parameter 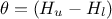 , so we will have to transform that back into our parameter of
interest at some point.
, so we will have to transform that back into our parameter of
interest at some point.
This is the the sole reason why the method setParameterTransformationFunction has been
implemented: transform the parameters estimated given the linear regressor, the observation covariance matrix and
prior distribution. As the transformations, it they do exist which is not compulsory, are expected to be done with
simple operations using constant values, they should not affect the covariance matrix of the posterior
multidimensional normal distribution, only the mean vector. The prototype of this function is as follows:
setParameterTransformationFunction(fTransfoParam)Its only argument is a pointer to the transformation function in the usual C++ prototype. This function provided to get the proper values of the under-investigation parameters take two arguments: the input parameters which are the raw one estimated from the analytical formula detailed in [metho] and the output ones, which should be the ones one wants to have. Both parameters are double-array whose size must be the number of parameters.
The example provided in the use-case is really simple as there is only one parameter to be estimated, which implies that both argument are one-dimension double array which should look like this:
void transf(double *x, double *res)
{
res[0] = 1050 - x[0]; // simply H_l = \theta - H_u
}
Warning
This is also possible in python but the transformation will still have to be the usual C++ one. To do so, the function has to be put in a C-file, for example calledmyFunction.C and this file has to be
loaded in order to get the handle on the function. Here are the few lines that summarise these two steps in a
fictional macro that would define a cal instance of TLinearBayesian:
# Define all the needed material: dataservers, models...
cal=Calibration.TLinearBayesian(...) # Create the instance and distance function
# ...
# Load the file in which Transformation function
ROOT.gROOT.LoadMacro("myFunction.C")
# Provide this function to the TLinearBayesian instance
cal.setParameterTransformationFunction(ROOT.transf)
When the estimation is done, it is possible to access the results numerically by calling three methods detailed
below. In all cases, the prototype is the same as these functions take no argument and return a
TMatrixD instance filled with corresponding information. The functions are:
- getParameterValueMatrix
It returns the raw value of the parameters, meaning the way they have been estimated through the analytical formula. It should return a
TMatrixDobject that should look like a vector (only one-varying dimension).- getParameterCovarianceMatrix
It returns the covariance matrix of the estimated parameters, which means that the
TMatrixDobject should be symmetrical and have a (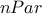 ,
, 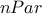 ) dimension.
) dimension.
- getTransfParameterValueMatrix
It returns the transformed value of the parameters, in case the
setParameterTransformationFunctionhas been called properly. It should return aTMatrixDobject that should look like a vector (only one-varying dimension).
The parameters can be drawn with the newly-defined instance of drawParameters whose
prototype is the same as the original one discussed in Section XI.2.3.6.
drawParameters(sTitre, variable = "*", select = "1>0", option = "")It takes up to four arguments, three of which are optional:
- sTitre
The title of the plot to be produced (an empty string can be put).
- variable
This field should contain the parameter list to be drawn (with the usual format of parameter's name splitted by ":"). The default value is to draw all parameters (the
"*"field).- select
A selection field to remove some kept configurations, which is useless in our case as no events are drawn, only analytical functions, see below.
- option
The optional field can be used to tune a bit the plots, options being separated by commas
"nonewcanvas": if this option is used the plot will be done in an existing canvas, if not, a new
TCanvaswill be created on the spot."vertical": if this option is used and more than one parameters have to be displayed, the canvas is splitted into as many windows as parameters in the variable list, the windows being stacked one above the others, using the full width. The default is "horizontal" so the plots are side-by-side.
"apriori/aposteriori": by default, both distributions are drawn. If this not what's wanted, it is possible to precise either "apriori" or "aposteriori".
"transformed": if this posteriori distribution has to be drawn, this option states that the transformed values should be used as the mean-vector of the multivariate normal posterior distribution.
The main difference with the usual instance of drawParameters defined in
TCalibration is that the object drawn are analytical functions.
On top of the parameters, the residues can also be drawn by calling the drawResidue method
and no modification has been done to it (for more details, see Section XI.2.3.7).
computePredictionVariance method:
computePredictionVariance(tdsPred, outname)- tdsPred
a dataserver that contains new location to be estimated and in which all regressors should be available in order to be able to compute the covariance matrix.
- outname
the name of the attribute that would be created and which will be filled with the diagonal part (the variance) of the
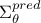 matrix.
matrix.






