Documentation
/ Manuel utilisateur en Python
: 
| XI.6. The Markov-chain approach | ||
|---|---|---|
 | Chapter XI. The Calibration module |  |
Unlike the Monte-Carlo methods already discussed in Chapter III to obtain design-of-experiments and which usually provides independent samples (which means that the successive observations are statistically independent unless correlation is purposely injected), the Monte-Carlo techniques describe here are called "Markov-chain" and they provide dependent samples as the estimation of the i-Th iteration only depends of the value of the previous one, the (i-1)Th. The method presented here, so far just the Metropolis-Hasting algorithm, is a way to generate posterior distributions from a priori and data under the assumption that the residues are Gaussian (see [metho] for a brief introduction and more useful references).
The way to use our Metropolis-Hasting class is summarised in few key steps here:
Get the reference data, the model and its parameters. The parameters to be calibrated must be
TStochasticAttribute-inheriting instances. Choose the assessor type you'd like to use and construct theTMetropHastingobject accordingly with the suitable distance function. Even though this mainly relies on common code, this part is introduced also in Section XI.6.1, in particular for what happened to the distance function (pay attention to the warning bloc)..Provide algorithm properties (not mandatory), to define optional behaviour and precise the uncertainty hypotheses you want, through the methods discussed in Section XI.6.2.
Finally the estimation is performed and the results can be extracted or draw with the usual plots. The specificities are discussed in Section XI.6.3.
A special step has to be considered for post-processing. As long as you have your
TMetropHasting-instance, even though you have exported you parameterTDataServerto be sure that you have it (this should always be done), the you can investigate the quality of the sample through a plot and functions, see Section XI.6.3 for more details.
The constructors that can be used to get an instance of the TMetropHasting class are those
detailed in Section XI.2.3. As a reminder the prototype available are these ones:
# Constructor with a runner
TMetropHasting(tds, runner, ns=1, option="");
# Constructor with a TCode
TMetropHasting(tds, code, ns=1, option="");
# Constructor with a function using Launcher
TMetropHasting(tds, fcn, varexpinput, varexpoutput, ns=1, option="");
The details about these constructor can be found in Section XI.2.3.1, Section XI.2.3.2 and Section XI.2.3.3
respectively for the TRun, TCode and
TLauncherFunction-based constructor. In all cases, the number of samples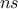 
has to set and represents the number of
configurations kept in the final sample.
As for the option, there is a specific option which might be used to change the default value of the a posteriori behaviour. The final sample is a distribution of the parameters value and if one wants to investigate the impact of the a posteriori measurement, two possible choice can be made to get a single-point estimate that would best describes the distribution:
use the mean of the distribution: the default option chosen
use the mode of the distribution: the user needs to add "mode" in the option field of the
TMetropHastingconstructor.
The default solution is straightforward, while the second needs an internal smoothing of the distribution in order to get the best estimate of the mode.
The final step here it to construct the TDistanceFunction which is the compulsory step which
should always come right after the constructor, but a word of caution about this step:
Warning
Whatever the distance function you're choosing, thesetDistanceAndReference is locally
redefined so that the distance function will only be a TWeightedLSDistanceFunction. As
stated previously, the underlying hypotheses here is that the residue under investigation is
normally-distributed. The user is requested to provide a guessed uncertainty (which does not have to be constant
throughout the reference observation datasets, but could be) to ponderate the difference (as it should reflect the
uncertainty coming from the model misknowledge and / or those affecting the observations). This is discussed in
details in [metho] but the idea is to summarise the ratio of the likelihood (the newly tested configuration,
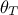with respect
to the latest one kept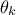 
) which allows to get rid of constant factors and should look like this once transformed to its
log form:
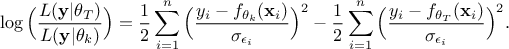
Once the TMetropHasting instance is created along with its
TDistanceFunction, there are few methods that can be of use in order to tune the algorithm
parameters. All these methods are optional in the sens that there are default value, each are detailed in the
following sub-sections.
The first method discussed here is rather simple: a Markov-Chain method might be rather long to estimate, particularly when running a code, whatever the chosen architecture. This method just change the printing message showing how well the algorithm is converging. The prototype is simply this one
setNbDump(nbDump)in which the only argument is the modulo to which the algorithm will display where it stands. The default value being 1000, the output should starts like this:
1000 events done 2000 events done 3000 events done ...
As already explained in [metho], the random walk algorithm starts at a given point and then move from there to the
new configuration. This means that two things have to be precised for every single parameters: a starting value,
and a variation range used to move to the next location. All the input parameters being stochastic (or in other
way, they're all instance of TStochasticDistribution-inheriting classes), the default values are
randomly drawn for the starting point values;
the theoretical standard deviation as variation range.
The default behaviour can easily be overcome by calling the setInitialisation method with
one of these two prototypes:
# Protoype with arrays constructed as, for instance
# values = np.array([0.8, -0.6])
# stands = np.array([0.4, 0.5])
setInitialisation(n, values, stands)
# Protoype with two vectors consructed for instance as
# values = ROOT.std.vector['double']([0.8, -0.6])
# stands = ROOT.std.vector['double']([0.4, 0.5])
setInitialisation(values, stands) # both parameters are vector
The first one is using simple arrays with a first argument being their size, the second one is safer as the simple
of the collection is embedded within the collection itself (the existence of these two prototypes is relevant
because of python-binding). Disregarding these technical details, the first argument should contains the starting
point of all parameters while the second one contains their variation range meaning that both arrays or vector,
should have the size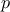 
.
As also explained in [metho], there are theoretical discussion on the acceptation rate expected, depending on the dimension of the parameter space for instance. As stated in some references (see [gelman1996efficient,roberts1997weak]) when well initialised, a-single dimension problem acceptation rate could be around 44% and this should go down to 23% as the dimension increases. By default, the exploration parameters are set by the initialisation step (as discussed in Section XI.6.2.2
If one wants to change this, a possible handle would be to use the
setAcceptationRatioRange method whose prototype is the following
setAcceptationRatioRange(lower, higher)
This prototype takes two argument: the lower (
) and higher (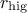
) bounds. The idea is simply that after a certain number of estimation (called
batch, whose value is set to 100) the algorithm looks at the acceptation rate achieved
(actually this is computed for every configuration and kept in the final TDataServer object). If the lower and higher
bounds have been set, at the end of a batch, three cases are possibles (when the acceptation rate is called
):
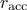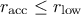: the acceptation rate is too low with respect to your goal, which means that you might be
moving to far when moving from the latest conserved configuration. As a consequence, the variation range is
reduced by 10% to help convergence.
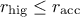: the acceptation rate is too high with respect to your goal, which means that you might not
be exploring the parameter space as you should, only investigating a nicely working area. As a consequence,
the variation range is increased by 10% to help the exploration.
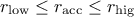: the acceptance rate is the desired range, so nothing's done.
When the setAcceptationRatioRange method has been called, this process will be called at
the end of every batch. Otherwise, the default behaviour is to let the
acceptation rate as it is, has no boundaries have been set.
Few words of caution: obviously, from the prototype and the behaviour discussed above, there are two rules that
should be followed when using this metho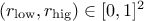d: 
and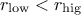 
.
Finally, one can have a look at the evolution of the acceptation rate by plotting the information, as discussed in Section XI.6.3.2.
Finally once the computation is done there are three different kinds of results and several ways to interpret but also transform it. This section details some important and specific aspect to it. The first thing to keep in mind is the fact that this method should lead to a sample of configurations. This sections introduces first quality investigation for the provided sample and then ways to illustrate these results.
Once the algorithm has stopped, the first thing to check is the quality of the sample which can be assessed by different ways. Let's start by introducing the theoretical aspects: when discussing the sample two parameters might be of interest
the burn-in (also called warm-up): it corresponds to the number of iteration needed to reached a suitable approximation of the target density (see [metho]). This has to be defined by the user mainly from the trace plot (discussed below, see Section XI.6.3.1).
the auto-correlation: the idea behind this is to estimate how self-correlated the samples are. The argument called lag can be used to thin the sample, see the discussion in the dedicated section Section XI.6.3.3.
The trace plot is simply the evolution of the value of each parameter as a function of the iteration number. The idea is to get a glimpse at two information:
a possible bad behaviour in the low iteration region that could arise because the algorithm is supposed to converge to the targeted density after a certain number of attempts (see [metho]), which should lead to the definition of the burn-in
a possible correlation between the estimations (spacial one) that could give hint to a lag estimation if needed but also to increase the burn-in if peculiar behaviour is seen.
The method to do this is called drawTrace and as the following prototype:
drawTrace(sTitre, variable = "*", select = "1>0", option = "")It takes up to four arguments, three of which are optional:
- sTitre
The title of the plot to be produced (an empty string can be put).
- variable
This field should contain the parameter list to be drawn (with the usual format of parameter's name splitted by ":"). The default value is to draw all parameters (the
"*"field).- select
A selection field to remove some kept configurations for instance if you want to consider the burn-in period or lag procedure.
- option
The optional field can be used to tune a bit the plots, options being separated by commas
"nonewcanvas": if this option is used the plot will be done in an existing canvas, if not, a new
TCanvaswill be created on the spot."vertical": if this option is used and more than one parameters have to be displayed, the canvas is splitted into as many windows as parameters in the variable list, the windows being stacked one above the others, using the full width. The default is "horizontal" so the plots are side-by-side.
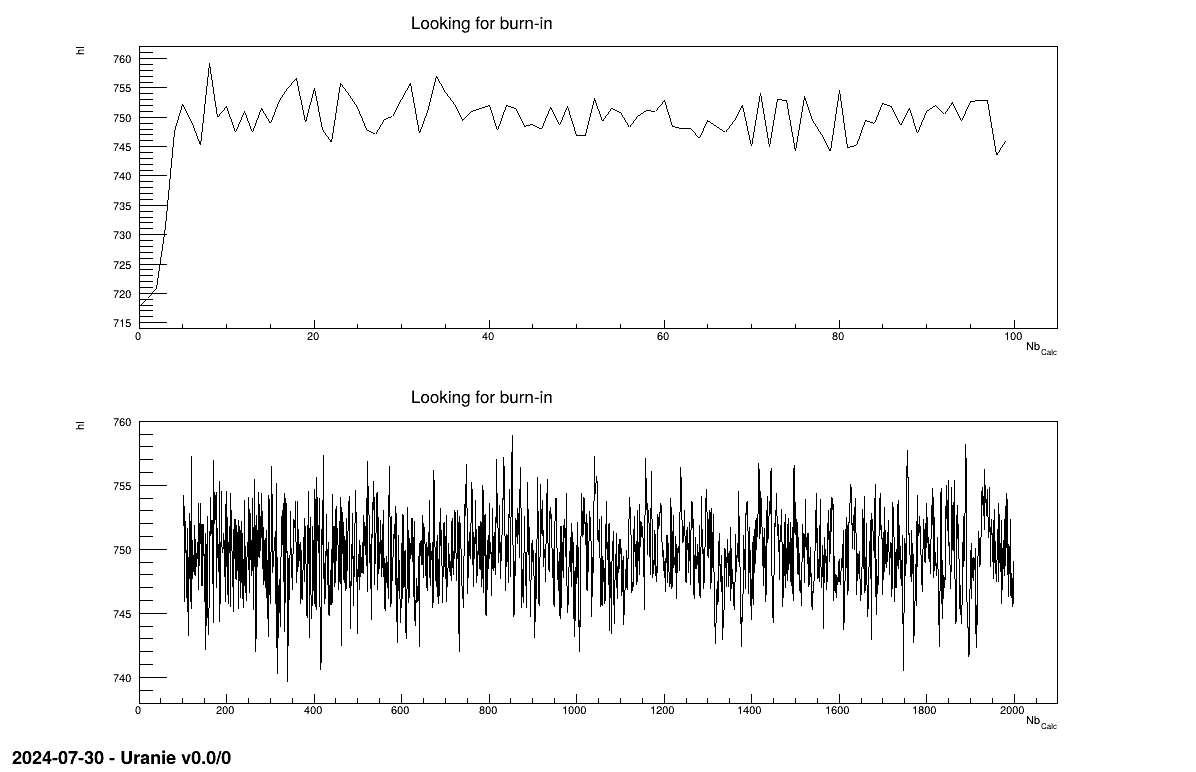
Taking back the example shown in Section XIV.12.4, one can split the trace plots (originally shown in Figure XIV.101) into two regions using the selection argument. The first guess chosen here is to split events below and above a threshold of 100 events with the following code, leading to Figure XI.2
cantr = ROOT.TCanvas("cantr", "cantr", 1200, 800)
pad = ROOT.TPad("pad", "ppad", 0, 0.03, 1, 1)
pad.Draw()
pad.cd()
pad.Divide(1,2)
pad.cd(1)
cal.drawTrace("Looking for burn-in", "*", "%s < 100" % (tdsPar.getIteratorName()), "nonewcanvas")
pad.cd(2)
cal.drawTrace("Looking for burn-in", "*", "%s > 100" % (tdsPar.getIteratorName()), "nonewcanvas")
From Figure XI.2, one can see, from the top pad, that the very beginning seem
wrong, as too far away (probably an initialisation far from the more probable value) and then the behaviour seem
fine as it evolves around what's seems to be the most probable value going back and forth. From there a very small
burn-in of for example 20 can be chosen. Once this value is chosen it can be provided back to the calibration
object and it will be used in many drawing methods as part of the default cut value. This can be done by calling
the setBurnin method whose signature is the following one
setBurnin(burnin)
Warning
Setting a burnin value with thesetBurnin method will affect most the drawing method, and one should
see a line that state what's the default cut used (either burnin or lag selection) to produce a plot. Only the
residues plot will not be affected as the a posteriori residues are computed during the
estimateParameters methods, so prior to any burnin or lag determination. If one wants to re-estimate
residues with a given set of parameters that takes into account either lag or burnin, use the 3
estimateCustomResidues method discussed in Section XI.2.3.5.
If one wants to get rid of current cut, use the clearDefaultCut method that does not require any
argument and whose purpose is to remove both lag and burnin:
clearDefaultCut()
The acceptation ratio plot is simply the evolution of this value for each parameter as a function of the iteration number. The idea is to get a glimpse at two information:
a possible bad behaviour in the low iteration region that could arise because the algorithm is supposed to converge to the targeted density after a certain number of attempts (see [metho]), which might lead to the definition of the burn-in (if the acceptance range has not been tuned by calling the method introduced in Section XI.6.2.3).
check that the acceptance ratio target you'd like to have is achieved (and guess the impact on your variation range guess).
The method to do this is called drawAcceptationRatio and as the following prototype:
drawAcceptationRatio(sTitre, variable = "*", select = "1>0", option = "")It takes up to four arguments, three of which are optional:
- sTitre
The title of the plot to be produced (an empty string can be put).
- variable
This field should contain the parameter list to be drawn (with the usual format of parameter's name splitted by ":"). The default value is to draw all parameters (the
"*"field).- select
A selection field to remove some kept configurations for instance if you want to consider the burn-in period or lag procedure.
- option
The optional field can be used to tune a bit the plots, options being separated by commas
"nonewcanvas": if this option is used the plot will be done in an existing canvas, if not, a new
TCanvaswill be created on the spot."vertical": if this option is used and more than one parameters have to be displayed, the canvas is splitted into as many windows as parameters in the variable list, the windows being stacked one above the others, using the full width. The default is "horizontal" so the plots are side-by-side.
This is illustred in Section XIV.12.5 that show another very simple use-case with two paramters to be estimated at once, run in C++ and python.
As stated previously, a correlation between the estimations is expected because of the nature of the sampler: it is a Markov-chain so every new location depends only on its the previous one. Having an uncorrelated sample is a goal if one wants to use the standard deviation of the given sample to extract confidence interval for instance. The usual way to do is to test lag value, meaning using 1 events out of lag as sample.
To compute this, the method getAutoCorrelation whose prototype is
burn = 20 # Remove first 20 elements
lag = ROOT.std.vector('int')([1, 5, 10, 20]) # chosen lag
autoCorr = ROOT.std.vector['double'](range(lag.size())) # results of the following method
getAutoCorrelation(l, autoCorr, burn)It takes thee argument, one being optional:
a vector of integers containing the lag values one would like to investigate
a vector of double containing the auto-correlation computed with all the lag values provided. If there are more than one parameters, these auto-correlations are stored for the first parameters, with all lag values, then come the other parameter with their lag value, and so on...
Taking back the example shown in Section XIV.12.4, one can look at the console in Section XIV.12.4.3 to see the values for our simple case which shows and state that a lag of 5 is well enough to get an uncorrelated sample. In this case, the final sample would be thinned to get only one event out of 5, for instance using a selection of this kind
lag = 5
thin_cut = "(%s %% %d) == 0 " %(tdsPar.getIteratorName(), lag)
Warning
This approach is sometimes discussed as people might choose very large lag values which is very crude way, because the auto-correlation might arise from a wrong choice of variation range for instance. For more discussion on this, please look at [link2012thinning]. Once this value is chosen it can be provided back to the calibration object and it will be used in many drawing methods as part of the default cut value. This can be done by calling thesetLag method whose signature is the following one
setLag(lag)Warning
Setting a lag value with thesetLag method will affect most the drawing method, and one should see a
line that state what's the default cut used (either burnin or lag selection) to produce a plot. Only the residues
plot will not be affected as the a posteriori residues are computed during the
estimateParameters methods, so prior to any burnin or lag determination. If one wants to re-estimate
residues with a given set of parameters that takes into account either lag or burnin, use the 3
estimateCustomResidues method discussed in Section XI.2.3.5.
If one wants to get rid of current cut, use the clearDefaultCut method that does not require any
argument and whose purpose is to remove both lag and burnin:
clearDefaultCut()
The residues can be drawn with the classical instance of drawResidues whose arguments and
options have been introduced in details in Section XI.2.3.6, and whose
prototype is recalled here for your convenience:
drawResidues(sTitre, variable = "*", select = "1>0", option = "")
As no specific implementations has been done, the only remaining thing to discuss is the way both the a
priori and a posteriori configuration are chosen. The former is just using the
initialisation of the parameters meaning that it either comes from the user through the method discussed in Section XI.6.2.2 or, if this method has not been called, it comes from a random drawing
following the a priori probability density provided. The latter, one the other hand, has also
been discussed in the constructor section of this class (see Section XI.6.1). By
default, the mean of the posterior will be used, whereas if the option "mode" is precised when constructing the
TMetropHasting object, the mode would be estimated and used instead.
To get an example of this function, one can have a look at Figure XIV.102.
The parameters can be drawn with the newly-defined instance of drawParameters whose
prototype is the same as the original one discussed in Section XI.2.3.6.
void drawParameters(sTitre, variable = "*", select = "1>0", option = "")
The only difference with the usual instance of drawParameters defined in
TCalibration is that the selection field (the third argument of the function) is now always
including an extra selection to take into account the burn-in period (to get a discussion on the burn-in definition
see Section XI.6.3).
To get an example of this function, one can have a look at Figure XIV.103.
| |  | |
| XI.5. The Approximation Bayesian Computation techniques (ABC) |  | Chapter XII. The Uncertainty modeler module |