Documentation / User's manual in Python :

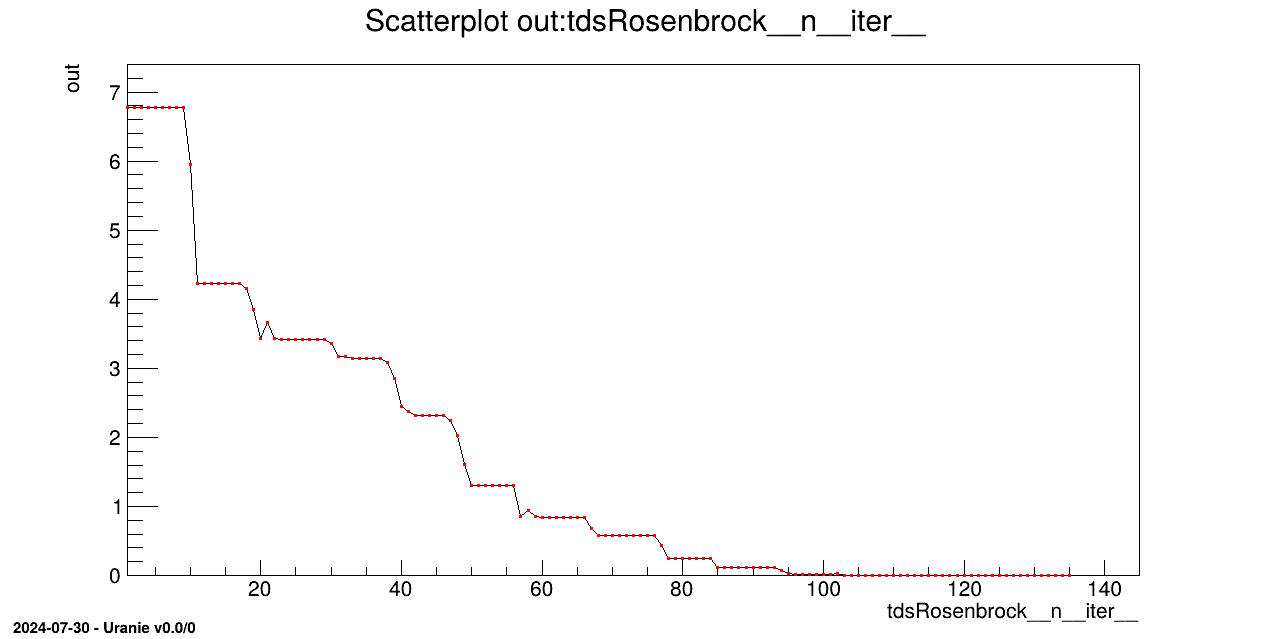
The objective of this macro is to perform a minimisation of a given function rosenbrock with the Migrad method.

"""
Example of function optimisation
"""
from rootlogon import ROOT, DataServer, Optimizer

# Load the function
ROOT.gROOT.LoadMacro("UserFunctions.C")

# Les variables de l'etude
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)

y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)

tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeFunctionRosenbrock",
                      5, 64, 1270, 667)

# Create an TOptimizer object from TDataServer and an anlystical function
topt = Optimizer.TOptimizer(tdsRos, "rosenbrock", "", "out")
# topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(1e-5)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)
topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")

The Rosenbrock's function is specified in the following file UserFunctions.C (the file can be found in ${URANIESYS}/share/uranie/macros). The UserFunctions.C is loaded to get the rosenbrock method:

gROOT.LoadMacro("UserFunctions.C");

The two TAttribute objects are the variables of the study: x and y. The intervals of definition and initial default values are set. The step value is set to 0.01 for the two variables:

x = DataServer.TAttribute("x", -1.5, 1.5);
x.setDefaultValue(-1.2);
x.setStepValue(0.01);

y = DataServer.TAttribute("y", -1.5,1.5);
y.setDefaultValue(1.);
y.setStepValue(0.01);

The TOptimizer object is initialised with the TDataServer containing both attributes, the name of the function to minimise, entry variables and output variable:

topt = Optimizer.TOptimizer(tdsRos, "rosenbronck", "", "out");
topt.optimize("same");

Results are exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

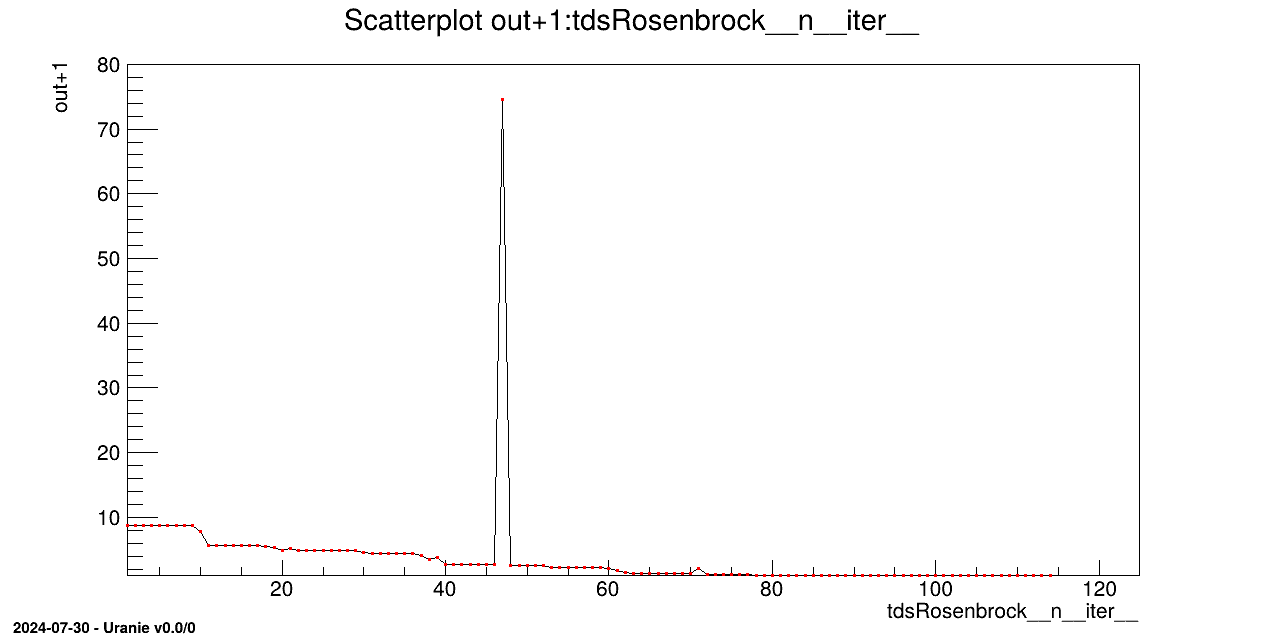
The objective of this macro is to perform a minimisation of a given function rosenbrock with the Migrad method. On top of the objective introduced in Section XIV.8.1.1, the idea is here to do the optimisation introducing new inputs (which are shifted values of the original ones) and add new output variables given simple mathematical formulae. Warning, this is slowing down the process as new values have to be computed on the fly, so we strongly recommend to change the loaded function instead. This functionnality has been introduced for consistency with the code optimisation.

"""
Example of function optimisation creating new inputs and outputs on the fly
"""
from rootlogon import ROOT, DataServer, Optimizer

# Load the function
ROOT.gROOT.LoadMacro("UserFunctions.C")

# Les variables de l'etude
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)

y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)

tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

tdsRos.addAttribute("xshift", "x-0.1")
tdsRos.addAttribute("yshift", "y+0.2")

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeFunctionRosenbrockNewInputOutput",
                      5, 64, 1270, 667)

# Create an TOptimizer object from TDataServer and an anlystical function
topt = Optimizer.TOptimizer(tdsRos, "rosenbrock", "xshift:yshift", "out")
topt.addOutputVariable("out+1:out*out:out*3")
topt.selectCost("out+1")
# topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(1e-5)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)
topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")

The main differences with Section XIV.8.1.2 are gathered in the next few blocks. It starts with the introduction of the new input attributes, defined through formulae:

tdsRos.addAttribute("xshift","x-0.1");
tdsRos.addAttribute("yshift","y+0.2");

The fact that the optimisation should be done on these newly defined variables is precised in the construction of the optimizer:

topt = Optimizer.TOptimizer(tdsRos, "rosenbronck", "xshift:yshift", "out");

The new output variables are defined through a dedicated method and the variable upon which the optimisation is performed is specified thanks to the selectCost function:

topt.addOutputVariable("out+1:out*out:out*3");
topt.selectCost("out+1");

The rest is consistent with what's done in Section XIV.8.1.2.

tdsRos.exportData("_tds_rosenbrock_.dat");

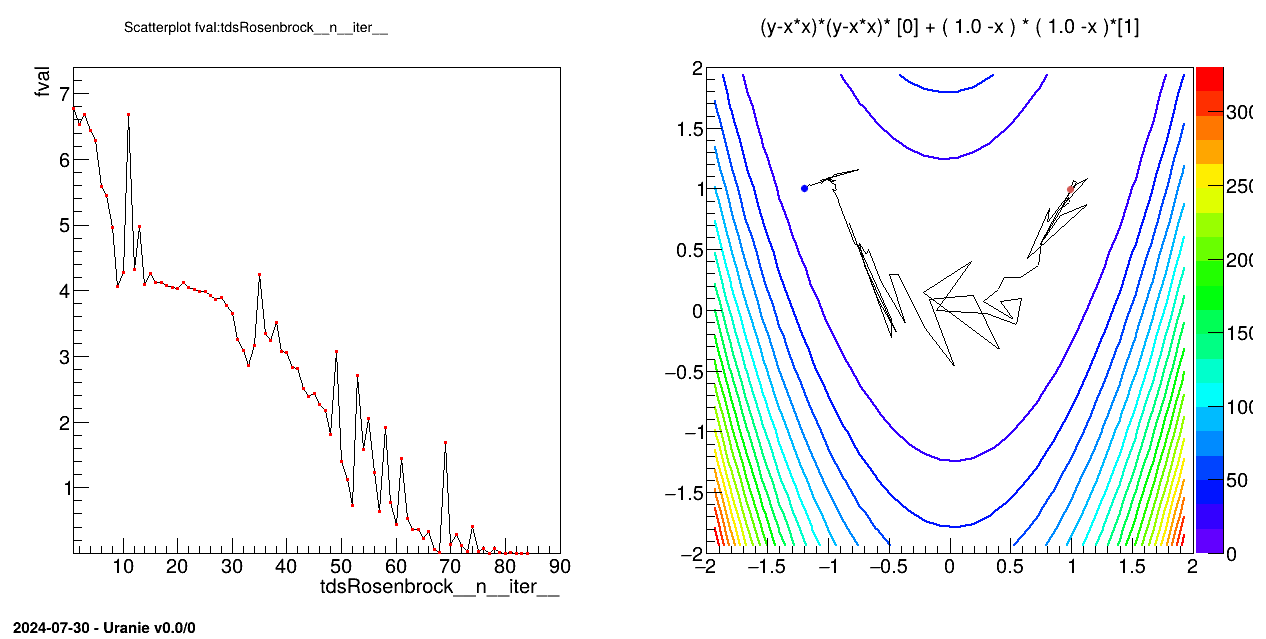
The objective of this macro is to perform an optimisation of the rosenbrock function returned by the rosenbrock code (described in Section VII.2.1.3) with the values of the two attributes x and y read in an input file with "key=value" format, input_rosenbrock_with_keys.dat:

#
# 
# inputfile for the \b rosenbrock code
# \date   mar jui 3 14:38:43 2007
# the two parameters
#

x  = -1.20 ; 
y  = 1.0 ;
a = 10.0 ;
b = 1.0 ;

The output file, _output_rosenbrock_with_keys_.dat, is with "key=value" format and looks like:

X = -1.200000e+000 ;
Y = 1.000000e+000 ;
fval = 6.776000e+000 ;
fA = 1.000000e+001 ; 
fB = 1.000000e+000 ;
	  

where fA and fB are parameters of the rosenbrock function. X and Y are the values of attributes x and y, fval the cost variable.

"""
Example of code optimisation with key input
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# The x attribute of the use case
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)
x.setFileKey("input_rosenbrock_with_keys.dat")

# The y attribute of the use case
y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)
y.setFileKey("input_rosenbrock_with_keys.dat")

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

# The output file of the code where values are stored in (key = value) format
fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat")
fOutputFile.addAttribute(DataServer.TAttribute("fval"))

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -k")
# The working directory to launch the code
# myRosenbrockCode.setWorkingDirectory(ROOT.gSystem.Getenv("PWD") +
#                                      TString("/tmpLanceurUranie/rosenbrock"))
# Add the output file
myRosenbrockCode.addOutputFile(fOutputFile)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeCodeRosenbrockKey",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)
topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(1e-5)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)

topt.optimize("same")
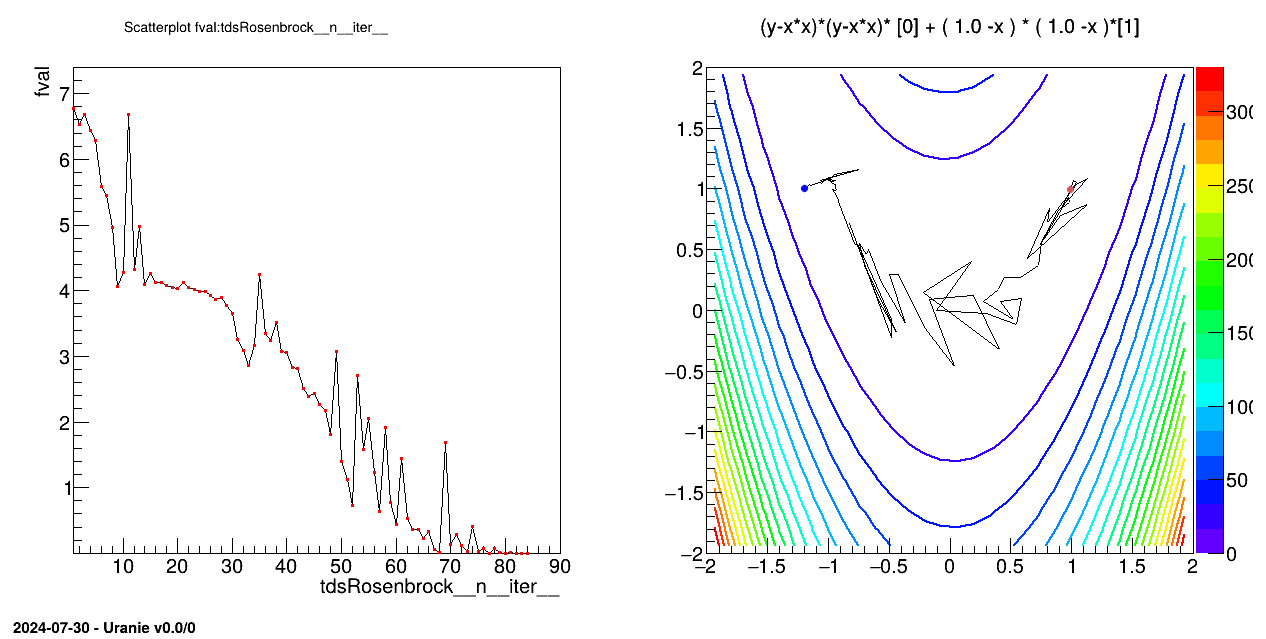
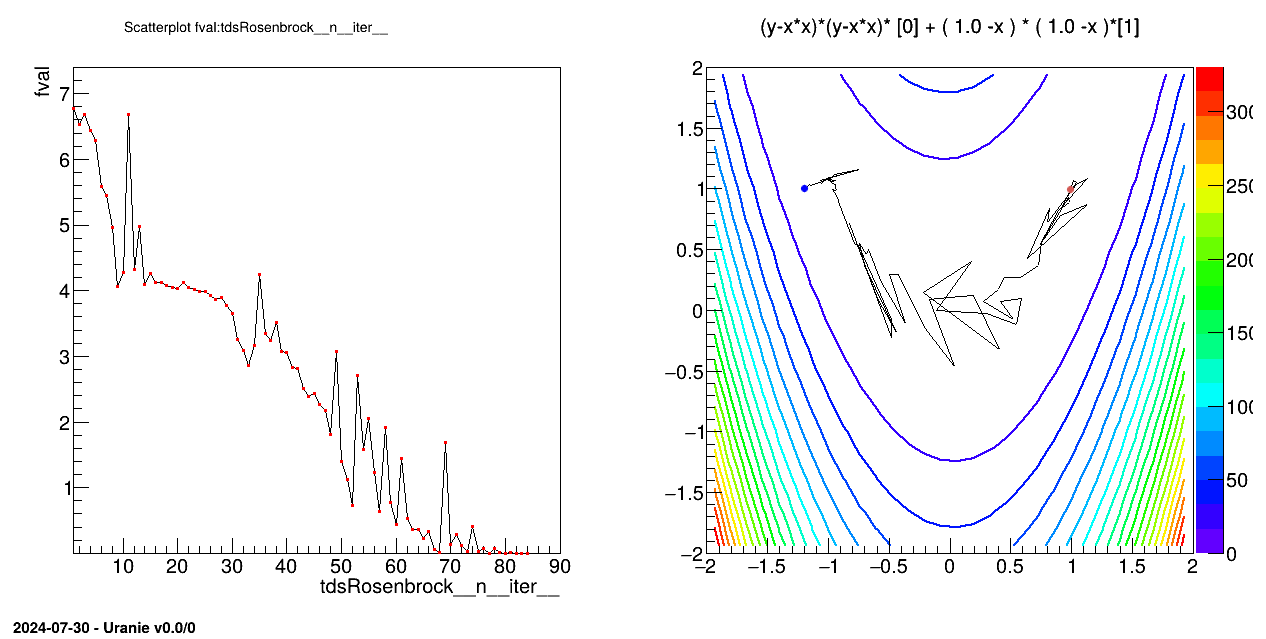
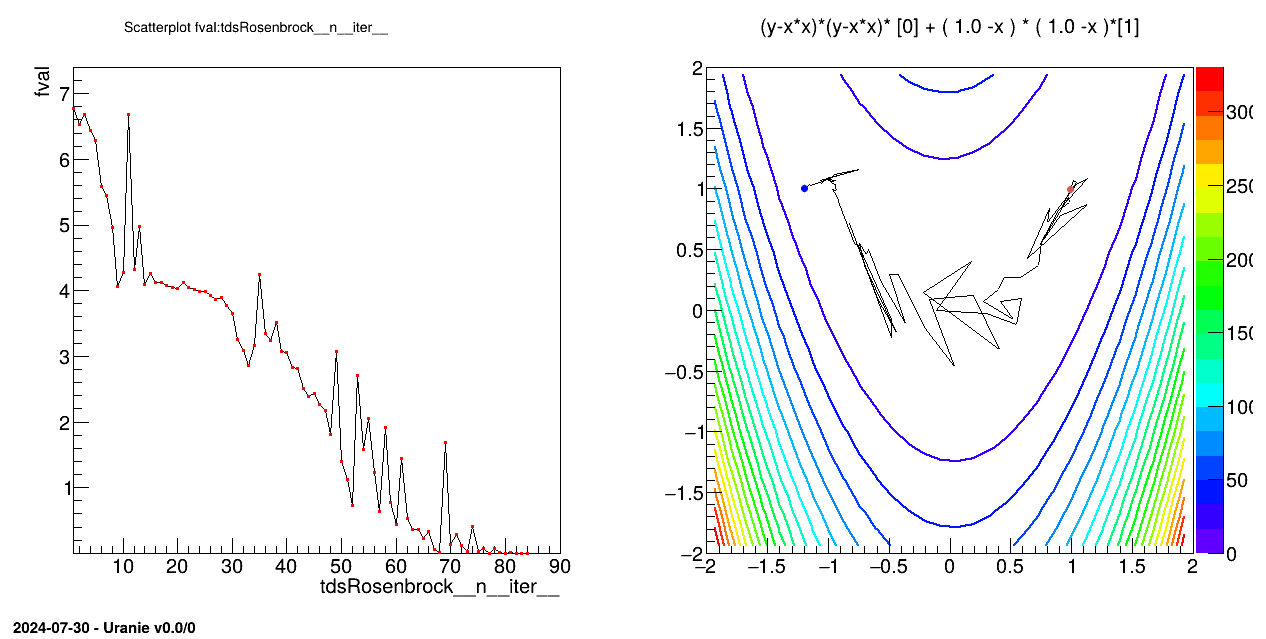
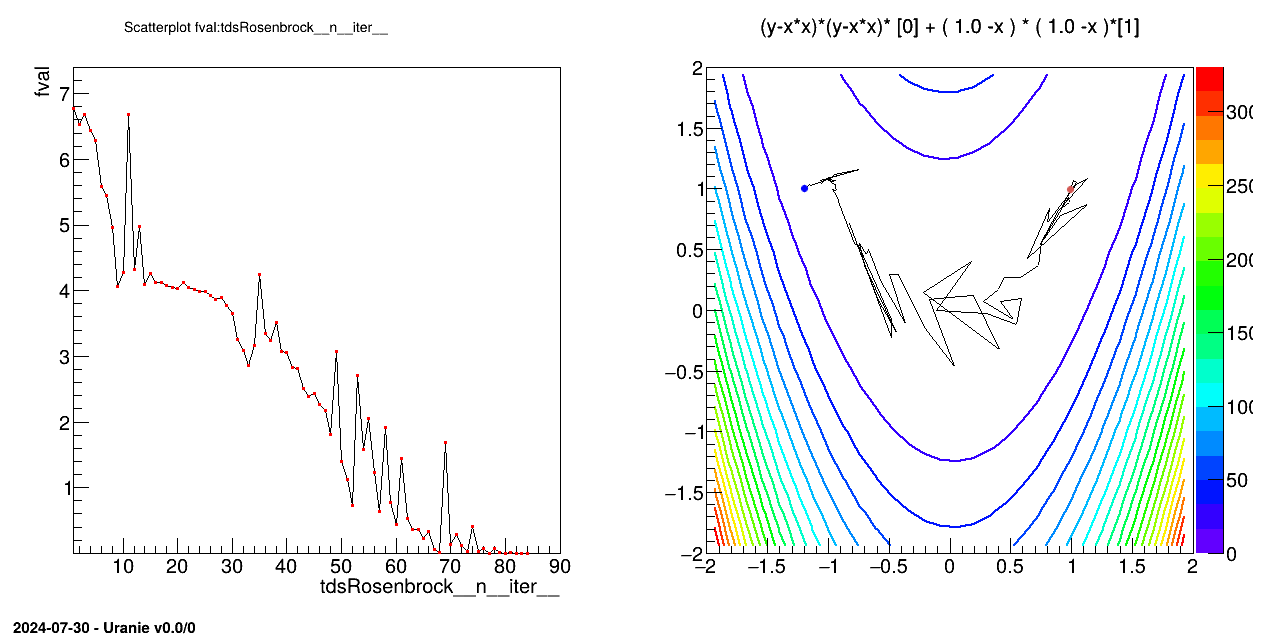
tdsRos.exportData("_tds_rosenbrock_.dat")

pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The TAttribute objects x and y are linked to the input file input_rosenbrock_with_keys.dat:

x = DataServer.TAttribute("x", -1.5, 1.5);
x.setDefaultValue(-1.2);
x.setStepValue(0.01);
x.setFileKey("input_rosenbrock_with_keys.dat");

y = DataServer.TAttribute("y", -1.5,1.5);
y.setDefaultValue(1.);
y.setStepValue(0.01);
y.setFileKey("input_rosenbrock_with_keys.dat");

Instantiating the output file:

fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat");

The cost variable is added to the output file as a new TAttribute:

fOutputFile.addAttribute(DataServer.TAttribute("fval"));

Instantiating the TCode object, the rosenbrock code is launched with the -k option. The input file searched by the code will then be with type "key=value":

myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -v -k");

The TOptimizer object is initialised with the TDataServer containing data and the TCode object. The optimisation is built with the Simplex method:

topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode);  
topt.setMethod(Optimizer.TOptimizer.kSimplex);
topt.optimize("same");

The TDataServer is exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

Processing optimizeCodeRosenbrockKey.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[x]
 ** input :: ivar[1/3] name[y]
 ** output :: ivar[2/3] name[fval]
 ** TMultiGenCode::init _sCost[fval] _nCost[ 1]
 ** _sCost[fval]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [84] option[Final]
 **   name [ x] Origin[kAttribute] Value[0.995289]
 **   name [ y] Origin[kAttribute] Value[0.99263]
 **   name [ fval] Origin[kAttribute] Value[6.34168e-05]
 ********** End Of Print state [84]

The objectives of this macro are the same as the ones detailed in Section XIV.8.3.1. On top of these, as for Section XIV.8.2.1, the idea is here to do the optimisation introducing new inputs (which are shifted values of the original ones) and add new output variables given simple mathematical formulae.

"""
Example of code optimisation with new input/output attributes
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# The x attribute of the use case
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)

# The y attribute of the use case
y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

tdsRos.addAttribute("xshift", "x-0.1")
tdsRos.getAttribute("xshift").setFileKey("input_rosenbrock_with_keys.dat", "x")
tdsRos.addAttribute("yshift", "y+0.2")
tdsRos.getAttribute("yshift").setFileKey("input_rosenbrock_with_keys.dat", "y")


# The output file of the code where values are stored in (key = value) format
fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat")
fOutputFile.addAttribute(DataServer.TAttribute("fval"))

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -k")
# The working directory to launch the code
# myRosenbrockCode.setWorkingDirectory(ROOT.gSystem.Getenv("PWD") +
#                                      TString("/tmpLanceurUranie/rosenbrock"))
# Add the output file
myRosenbrockCode.addOutputFile(fOutputFile)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeCodeRosenbrockKeyNewInputOutput",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and Launcher.TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)
topt.setMethod(Optimizer.TOptimizer.kSimplex)
topt.addOutputVariable("fval+1:fval*fval:fval*3")
topt.selectCost("fval+1")
topt.setTolerance(1e-3)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)

topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")


pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The main differences with Section XIV.8.4.2 are gathered in the next few blocks. It starts with the introduction of the new input attributes, defined through formulae. The new attributes are connected to the input file thanks to the setFileKey (and these methods are not called from the original attributes anymore):

tdsRos.addAttribute("xshift","x-0.1");
tdsRos.getAttribute("xshift").setFileKey("input_rosenbrock_with_keys.dat","x");
tdsRos.addAttribute("yshift","y+0.2");
tdsRos.getAttribute("yshift").setFileKey("input_rosenbrock_with_keys.dat","y");

Once settled, the remaining modifications to be done with respect to Section XIV.8.3.2 are the creation of the new output variables and the change of variable to be used as cost function.

topt.addOutputVariable("fval+1:fval*fval:fval*3");
topt.selectCost("fval+1");

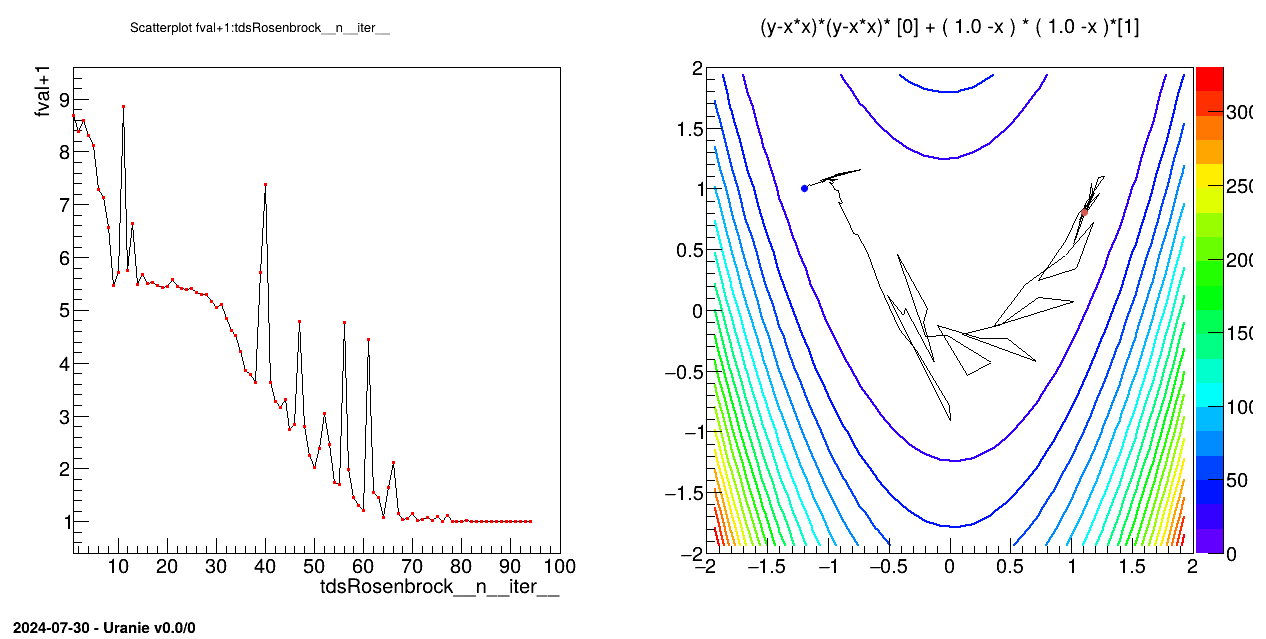
This, as for the use-case discussed in Section XIV.8.2, will lead to new results as shown in Section XIV.8.4.4: the minimisation is performed on the two new inputs, and the minimimun is found when these values are close to one. Looking at the original variables, the value toward which they converge is 1.1 and 0.8 respectively for 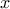and .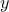

Processing optimizeCodeRosenbrockKeyNewInputOutput.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/8] name[x]
 ** input :: ivar[1/8] name[y]
 ** input :: ivar[2/8] name[xshift]
 ** input :: ivar[3/8] name[yshift]
 ** output :: ivar[4/8] name[fval]
 ** output :: ivar[5/8] name[fval+1]
 ** output :: ivar[6/8] name[fval*fval]
 ** output :: ivar[7/8] name[fval*3]
 ** TMultiGenCode::init _sCost[fval+1] _nCost[ 2]
 ** TMultiGenCode::init Creating the formula for new inputs 
 ** _sCost[fval+1]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval+1] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [94] option[Final]
 **   name [ x] Origin[kAttribute] Value[1.10427]
 **   name [ y] Origin[kAttribute] Value[0.808468]
 **   name [ fval+1] Origin[kAttribute] Value[1.00002]
 ********** End Of Print state [94]

The objective of this macro is to perform optimisation of the rosenbrock function returned by the rosenbrock code (described in Section VII.2.1.3) with the values of the two attributes x and y read in an input file with "key=value" format, input_rosenbrock_with_keys.dat:

#
# 
# inputfile for the \b rosenbrock code
# \date   mar jui 3 14:38:43 2007
# the two parameters
#

x  = -1.20 ; 
y  = 1.0 ;
a = 10.0 ;
b = 1.0 ;

The output file, _output_rosenbrock_with_values_rows_.dat, is with "values in rows" format and looks like

#COLUMN_NAMES: x | y | fval | pA | pB

-1.200000e+000	1.000000e+000	6.776000e+000	1.000000e+001	1.000000e+000
	  

where pA and pB are parameters of the rosenbrock function. X and Y are the values of attributes x and y, fval the cost variable.

"""
Example of code optimisation with row inputs
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# The x attribute of the use case
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)
x.setFileKey("input_rosenbrock_with_keys.dat")

# The y attribute of the use case
y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)
y.setFileKey("input_rosenbrock_with_keys.dat")

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

# The output file of the code where values are in row
fOutFile = Launcher.TOutputFileRow("_output_rosenbrock_with_values_rows_.dat")
fOutFile.addAttribute(DataServer.TAttribute("fval"), 3)

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -k")
# The working directory to launch the code
# myRosenbrockCode.setWorkingDirectory(ROOT.gSystem.Getenv("PWD") +
#                                      TString("/tmpLanceurUranie/rosenbrock"))
# Add the output file
myRosenbrockCode.addOutputFile(fOutFile)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeCodeRosenbrockRow",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)
topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(1e-5)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)

topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")

pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The TAttribute objects x and y are linked to the input file input_rosenbrock_with_keys.dat:

x = DataServer.TAttribute("x", -1.5, 1.5);
x.setDefaultValue(-1.2);
x.setStepValue(0.01);
x.setFileKey("input_rosenbrock_with_keys.dat");

y = DataServer.TAttribute("y", -1.5,1.5);
y.setDefaultValue(1.);
y.setStepValue(0.01);
y.setFileKey("input_rosenbrock_with_keys.dat");

Instantiating the output file:

fOutputFile = Launcher.TOutputFileRow("_output_rosenbrock_with_values_rows_.dat");

The cost variable is added to the output file as a new TAttribute:

fOutputFile.addAttribute(DataServer.TAttribute("fval"));

Instantiating the TCode object, the rosenbrock code is launched with the -k option. The input file searched by the code will then be with type "key=value":

myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -v -k");

The TOptimizer object is initialised with the TDataServer containing data and the TCode object. The optimisation is built with the Simplex method:

topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode);  
topt.setMethod(Optimizer.TOptimizer.kSimplex);
topt.optimize("same");

The TDataServer is exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

Processing optimizeCodeRosenbrockRow.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[x]
 ** input :: ivar[1/3] name[y]
 ** output :: ivar[2/3] name[fval]
 ** TMultiGenCode::init _sCost[fval] _nCost[ 1]
 ** _sCost[fval]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [84] option[Final]
 **   name [ x] Origin[kAttribute] Value[0.995289]
 **   name [ y] Origin[kAttribute] Value[0.99263]
 **   name [ fval] Origin[kAttribute] Value[6.34168e-05]
 ********** End Of Print state [84]

The objective of this macro is to perform optimisation of the rosenbrock function returned by the rosenbrock code (described in Section VII.2.1.3) with the values of the two attributes x and y each defined in two input files, one with "key=value" format, input_rosenbrock_with_keys.dat:

#
# 
# inputfile for the \b rosenbrock code
# \date   mar jui 3 14:38:43 2007
# the two parameters
#

x  = -1.20 ; 
y  = 1.0 ;
a = 10.0 ;
b = 1.0 ;

the other with "values in rows" format, input_rosenbrock_with_values_rows.dat:

-1.20 1.0

Only the option given to the rosenbrock code will determine the input file effectively used. The output file, _output_rosenbrock_with_keys_.dat, is with "key=value" format and looks like:

X = -1.200000e+000 ;
Y = 1.000000e+000 ;
fval = 6.776000e+000 ;
fA = 1.000000e+001 ; 
fB = 1.000000e+000 ;
	  

where fA and fB are parameters of the rosenbrock function. X and Y are the values of attributes x and y, fval the cost variable.

"""
Example of code optimisation with row output recreated
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# The x attribute of the use case
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)
x.setFileKey("input_rosenbrock_with_keys.dat")
x.setFileKey("input_rosenbrock_with_values_rows.dat", "x",
             "%e", DataServer.TAttributeFileKey.kNewRow)

# The y attribute of the use case
y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)
y.setFileKey("input_rosenbrock_with_keys.dat")
y.setFileKey("input_rosenbrock_with_values_rows.dat", "y",
             "%e", DataServer.TAttributeFileKey.kNewRow)

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)

# The output file of the code where values are stored in (key = value) format
fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat")
fOutputFile.addAttribute(DataServer.TAttribute("fval"))

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -r")
# Add the output file
myRosenbrockCode.addOutputFile(fOutputFile)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeCodeRosenbrockKeyRowRecreate",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)
topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(1e-5)
# topt.setPrintLevel(5)
# topt.setMaxIterations(3)
# topt.setMaxFunctionCalls(10)

topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")

pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The TAttribute objects x and y are linked to two input files input_rosenbrock_with_keys.dat with "key=value" format and input_rosenbrock_with_values_rows.dat with "values in rows" format:

x = DataServer.TAttribute("x", -1.5, 1.5);
x.setDefaultValue(-1.2);
x.setStepValue(0.01);
x.setFileKey("input_rosenbrock_with_keys.dat");
x.setFileKey("input_rosenbrock_with_values_rows.dat","x","%e",DataServer.TAttributeFileKey.kNewRow);

y = DataServer.TAttribute("y", -1.5,1.5);
y.setDefaultValue(1.);
y.setStepValue(0.01);
y.setFileKey("input_rosenbrock_with_keys.dat");
y.setFileKey("input_rosenbrock_with_values_rows.dat","y","%e",DataServer.TAttributeFileKey.kNewRow);

Instantiating the output file:

fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat");

The cost variable is added to the output file as a new TAttribute:

fOutputFile.addAttribute(DataServer.TAttribute("fval"));

Instantiating the TCode object, the rosenbrock code is launched with the -k option. The input file searched by the code will then be with type "key=value":

myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -v -k");

The TOptimizer object is initialised with the TDataServer containing data and the TCode object. The optimisation is built with the Simplex method:

topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode);  
topt.setMethod(Optimizer.TOptimizer.kSimplex);
topt.optimize("same");

The TDataServer is exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

Processing optimizeCodeRosenbrockKeyRowRecreate.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[x]
 ** input :: ivar[1/3] name[y]
 ** output :: ivar[2/3] name[fval]
 ** TMultiGenCode::init _sCost[fval] _nCost[ 1]
 ** _sCost[fval]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [84] option[Final]
 **   name [ x] Origin[kAttribute] Value[0.995289]
 **   name [ y] Origin[kAttribute] Value[0.99263]
 **   name [ fval] Origin[kAttribute] Value[6.34168e-05]
 ********** End Of Print state [84]

The objective of this macro is to perform optimisation of the rosenbrock function returned by the rosenbrock code (described in Section VII.2.1.3) with the values of the two attributes x and y read in an input file with "values in rows" format, input_rosenbrock_with_values_rows.dat, written on the fly:

-1.20 1.0

The output file, _output_rosenbrock_with_keys_.dat, is with "key=value" format and looks like:

X = -1.200000e+000 ;
Y = 1.000000e+000 ;
fval = 6.776000e+000 ;
fA = 1.000000e+001 ; 
fB = 1.000000e+000 ;
	  

where fA and fB are parameters of the rosenbrock function. X and Y are the values of attributes x and y, fval the cost variable.

"""
Example of code optimisation with row recreated input
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# The x attribute of the use case
x = DataServer.TAttribute("x", -1.5, 1.5)
x.setDefaultValue(-1.2)
x.setStepValue(0.01)
x.setFileKey("input_rosenbrock_with_values_rows.dat", "x",
             "%e", DataServer.TAttributeFileKey.kNewRow)

# The y attribute of the use case
y = DataServer.TAttribute("y", -1.5, 1.5)
y.setDefaultValue(1.)
y.setStepValue(0.01)
y.setFileKey("input_rosenbrock_with_values_rows.dat", "y",
             "%e", DataServer.TAttributeFileKey.kNewRow)

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(x)
tdsRos.addAttribute(y)


# The output file of the code where values are stored in (key = value) format
fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat")
fOutputFile.addAttribute(DataServer.TAttribute("fval"))

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -r")
# The working directory to launch the code
# myRosenbrockCode.setWorkingDirectory(ROOT.gSystem.Getenv("PWD") +
#                                      TString("/tmpLanceurUranie/rosenbrock"))
# Add the output file
myRosenbrockCode.addOutputFile(fOutputFile)

# Graph
Canvas = ROOT.TCanvas("c1", "Graph optimizeCodeRosenbrockRowRecreate",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)
topt.setMethod(Optimizer.TOptimizer.kSimplex)
#   topt.setTolerance(1e-5)
#   topt.setPrintLevel(5)
#   topt.setMaxIterations(3)
#   topt.setMaxFunctionCalls(10)

topt.optimize()
tdsRos.exportData("_tds_rosenbrock_.dat")

pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The TAttribute objects x and y are linked to the input file input_rosenbrock_with_values_rows.dat:

x = DataServer.TAttribute("x", -1.5, 1.5);
x.setDefaultValue(-1.2);
x.setStepValue(0.01);
x.setFileKey("input_rosenbrock_with_values_rows.dat","x","%e",DataServer.TAttributeFileKey.kNewRow);

y = DataServer.TAttribute("y", -1.5,1.5);
y.setDefaultValue(1.);
y.setStepValue(0.01);
y.setFileKey("input_rosenbrock_with_values_rows.dat","y","%e",DataServer.TAttributeFileKey.kNewRow);

Instantiating the output file:

fOutputFile = Launcher.TOutputFileKey("_output_rosenbrock_with_keys_.dat");

The cost variable is added to the output file as a new TAttribute:

fOutputFile.addAttribute(DataServer.TAttribute("fval"));

Instantiating the TCode object, the rosenbrock code is launched with the -r option. The input file searched by the code will then be with type "values in rows":

myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -v -r");

The TOptimizer object is initialised with the TDataServer containing data and the TCode object. The optimisation is built with the Simplex method:

topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode);  
topt.setMethod(Optimizer.TOptimizer.kSimplex);
topt.optimize("same");

The TDataServer is exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

Processing optimizeCodeRosenbrockRowRecreate.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[x]
 ** input :: ivar[1/3] name[y]
 ** output :: ivar[2/3] name[fval]
 ** TMultiGenCode::init _sCost[fval] _nCost[ 1]
 ** _sCost[fval]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [84] option[Final]
 **   name [ x] Origin[kAttribute] Value[0.995289]
 **   name [ y] Origin[kAttribute] Value[0.99263]
 **   name [ fval] Origin[kAttribute] Value[6.34168e-05]
 ********** End Of Print state [84]

The objective of this macro is to perform optimisation of the rosenbrock function returned by the rosenbrock code (described in Section VII.2.1.3) with the values of the two attributes x and y read in an input file with "values in rows" format, input_rosenbrock_with_values_rows.dat:

-1.20 1.0

written on the fly. The output file, _output_rosenbrock_with_values_rows_.dat, is with "values in rows" format (and instanced as a TOutputFileDataServer) looks like:

#COLUMN_NAMES: x | y | fval | pA | pB

-1.200000e+000	1.000000e+000	6.776000e+000	1.000000e+001	1.000000e+000
	  

where pA and pB are parameters of the rosenbrock function. X and Y are the values of attributes x and y, fval the cost variable.

"""
Example of code optimisation with recreated row input and dataserver output
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

sIn = ROOT.TString("input_rosenbrock_with_values_rows.dat")

# Define the DataServer and add the two attributes
tdsRos = DataServer.TDataServer("tdsRosenbrock", "Optimize Rosenbrock")
tdsRos.addAttribute(DataServer.TAttribute("x", -1.5, 1.5))
tdsRos.addAttribute(DataServer.TAttribute("y", -1.5, 1.5))

# The x attribute of the use case
tdsRos.getAttribute("x").setDefaultValue(-1.2)
tdsRos.getAttribute("x").setStepValue(0.01)
tdsRos.getAttribute("x").setFileKey(sIn, "x", "",
                                    DataServer.TAttributeFileKey.kNewRow)

# The y attribute of the use case
tdsRos.getAttribute("y").setDefaultValue(1.)
tdsRos.getAttribute("y").setStepValue(0.01)
tdsRos.getAttribute("y").setFileKey(sIn, "y", "",
                                    DataServer.TAttributeFileKey.kNewRow)

# The output file of the code where values are in row
oFil = Launcher.TOutputFileDataServer("_output_rosenbrock_with_values_rows_.dat")
oFil.addAttribute(DataServer.TAttribute("fval"))

# Create an Launcher.TCode object for my code
myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -r")
# The working directory to launch the code

# Add the output file
myRosenbrockCode.addOutputFile(oFil)

# Graph
Canvas = ROOT.TCanvas("c1",
                      "optimizeCodeRosenbrockRowRecreateOutputDataServer",
                      5, 64, 1270, 667)
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
pad.Divide(2, 1)
pad.cd(1)

# Create an TOptimizer object from TDataServer and TCode objects
topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode)

topt.setMethod(Optimizer.TOptimizer.kSimplex)
# topt.setTolerance(0.1)
topt.setMaxIterations(130)

topt.optimize("same")
tdsRos.exportData("_tds_rosenbrock_.dat")

pad.cd(2)
frosenbrok = ROOT.TF2("fcnRosenbrock",
                      "(y-x*x)*(y-x*x)* [0] + ( 1.0 -x ) * ( 1.0 -x )*[1]",
                      -2.0, 2.0, -2.0, 2.0)
frosenbrok.SetParameter(0, 10.0)
frosenbrok.SetParameter(1, 1.0)
frosenbrok.Draw("cont1z")
tdsRos.draw("y:x", "", "samel")

tdsRos.getTuple().SetMarkerColor(4)
tdsRos.getTuple().SetMarkerStyle(8)
tdsRos.getTuple().SetMarkerSize(.90)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"==1", "psame")
tdsRos.getTuple().SetMarkerColor(50)
tdsRos.Draw("y:x", tdsRos.getIteratorName()+"=="+str(tdsRos.getNPatterns()),
            "psame")

The TAttribute objects x and y are linked to the input file input_rosenbrock_with_values_rows.dat:

tdsRos = DataServer.TDataServer("tdsRos", "Optimize Code external Rosenbrock via TDataServer");
tdsRos.addAttribute(DataServer.TAttribute("x", -1.5, 1.5));
tdsRos.addAttribute(DataServer.TAttribute("y", -1.5, 1.5));

tdsRos.getAttribute("x").setDefaultValue(-1.2);
tdsRos.getAttribute("x").setStepValue(0.01);
tdsRos.getAttribute("x").setFileKey(sJDDReference,"x","",DataServer.TAttributeFileKey.kNewRow);

tdsRos.getAttribute("y").setDefaultValue(1.);
tdsRos.getAttribute("y").setStepValue(0.01);
tdsRos.getAttribute("y").setFileKey(sJDDReference,"y","",DataServer.TAttributeFileKey.kNewRow);

Instantiating the output file:

fOutputFile = Launcher.TOutputFileDataServer("_output_rosenbrock_with_values_rows_.dat");

The cost variable is added to the output file as a new TAttribute:

fOutputFile.addAttribute(DataServer.TAttribute("fval"));

Instantiating the TCode object, the rosenbrock code is launched with the -r option. The input file searched by the code will then be with type "values in rows":

myRosenbrockCode = Launcher.TCode(tdsRos, "rosenbrock -v -r");

The TOptimizer object is initialised with the TDataServer containing data and the TCode object. The optimisation is built with the Simplex method:

topt = Optimizer.TOptimizer(tdsRos, myRosenbrockCode);  
topt.setMethod(Optimizer.TOptimizer.kSimplex);
topt.optimize("same");

The TDataServer is exported in an ASCII file:

tdsRos.exportData("_tds_rosenbrock_.dat");

Processing optimizeCodeRosenbrockRowRecreateOutputDataServer.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Simplex]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[x]
 ** input :: ivar[1/3] name[y]
 ** output :: ivar[2/3] name[fval]
 ** TMultiGenCode::init _sCost[fval] _nCost[ 1]
 ** _sCost[fval]
 ********** Print state [0] option[Init]
 **   name [ x] Origin[kAttribute] Value[-1.2]
 **   name [ y] Origin[kAttribute] Value[1]
 **   name [ fval] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [84] option[Final]
 **   name [ x] Origin[kAttribute] Value[0.995289]
 **   name [ y] Origin[kAttribute] Value[0.99263]
 **   name [ fval] Origin[kAttribute] Value[6.34168e-05]
 ********** End Of Print state [84]

This part introduces the logic of the upcoming examples in Section XIV.8.10 and Section XIV.8.11. We consider here that the myCode external code depends on three parameters, a, b and c, and we want to find the values of these parameters that best fit a reference set of values.

tds = DataServer.TDataServer()                                 
tds.addAttribute(DataServer.TAttribute("a", -5.0, 5.0))
tds.addAttribute(DataServer.TAttribute("b", -1.0, 1.0))
tds.addAttribute(DataServer.TAttribute("c", -5.0, 5.0))

# The reference input file                                            
sJDDReference = gSystem.pwd() + "/myCode_param.in"
tds.getAttribute("a").setFileKey(sJDDReference,"a")
tds.getAttribute("b").setFileKey(sJDDReference,"b")
tds.getAttribute("c").setFileKey(sJDDReference,"c")

tds.getAttribute("a").setDefaultValue(0.200)
tds.getAttribute("a").setStepValue(0.01)
tds.getAttribute("b").setDefaultValue(0.200)
tds.getAttribute("b").setStepValue(0.01)
tds.getAttribute("c").setDefaultValue(0.200)
tds.getAttribute("c").setStepValue(0.01)

# The output file of the code                                         
fout = Launcher.TOutputFileRow("myCode_output.dat")
# The attribute in the output file
fout.addAttribute(DataServer.TAttribute("yhat"))

mycode = Launcher.TCode (tds, "myCode >> /dev/null")                
mycode.addOutputFile( fout )

# Read the reference dataserver, that contains the "ystar" attribute
tdsref = DataServer.TDataServer("TDSRef", "Objectives values")  
tdsref.fileDataRead("myCode_ref.dat")

# Definition of the optimizer
topt = Optimizer.TOptimizer(tds, mycode)                       
topt.addObjective( "obj1", tdsref, "ystar", fout, "yhat")            
topt.optimize()                                                      

Considering the rosenbrock code example. We have generated a set of values with parameters a and b fixed, and stored both input and output values in the file rosenbrock_ref.dat:

#NAME: testRosenbrock
#TITLE: Rosenbrock
#DATE: mar sep 25 15:30:20 CEST 2012
#COLUMN_NAMES: x1| x2| y

-1.350076223e+00 3.365490640e-01 1.767170212e+01
1.183157479e+00 -6.425784534e-01 1.258177769e+01
-9.634946792e-01 -1.301159335e+00 2.262238374e+01
1.522053698e+00 -4.413296049e-01 2.336439261e+01
-5.921963897e-01 -1.189104788e+00 1.218314329e+01
7.477007261e-01 4.940760535e-01 1.399771741e-01
1.461164459e+00 9.121608682e-01 4.911363513e+00
3.793243287e-01 1.623933752e+00 7.342092216e+00
-1.713026222e+00 -4.397660890e-01 4.887720411e+01
1.228036214e+00 1.425142762e-01 5.698252451e+00
-1.327069995e+00 1.133228437e+00 1.201323326e+01
1.465765779e+00 -4.783690687e-01 2.113471528e+01
-2.659000948e-01 -3.717979765e-01 3.792427072e+00
1.326644911e+00 -6.113681370e-02 1.016286658e+01
-5.986060012e-01 -1.611296639e+00 1.674935948e+01
-8.026301529e-01 3.762660855e-02 7.602799958e+00

The rosenbrock code is only able to take one set of parameters (a,b) at each call, and returns only one value each time. In order for Uranie to find the parameters that best fit the results above, it is necessary to add a level of "code" that will be able to compute a set of outputs from a set of inputs. This new "code" will be the Uranie macro discussed in the C++ version of this manual.

Now that we have an external code (the ROOT macro just defined above), we can use the same optimisation scheme than the one described in Section XIV.8.9, but the code to run will be the ROOT macro execution:

"""
Example of code optimisation multi level
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer

# Definition of the dataserver
tds = DataServer.TDataServer()

# Definition of the attributes
sJDDReference = "input_rosenbrock_with_keys.dat"
tds.addAttribute(DataServer.TAttribute("a", 0.0, 5.0))
tds.getAttribute("a").setFileKey(sJDDReference, "a")
tds.getAttribute("a").setDefaultValue(1.0)
tds.getAttribute("a").setStepValue(0.1)
tds.addAttribute(DataServer.TAttribute("b", 0.0, 5.0))
tds.getAttribute("b").setFileKey(sJDDReference, "b")
tds.getAttribute("b").setDefaultValue(2.0)
tds.getAttribute("b").setStepValue(0.1)

# Definition of the output file of the code
fout = Launcher.TOutputFileRow("_rosenbrock_multi_.dat")
fout.addAttribute(DataServer.TAttribute("yhat"), 3)

# Definition of the code
to_null = " > NUL" if ROOT.gSystem.GetBuildArch() == "win64" else " >> /dev/null"
mycode = Launcher.TCode(tds, "root -b -l -q rosenbrock_multi.C" + to_null)
mycode.addOutputFile(fout)
mycode.addInputFile("rootlogon.C")
mycode.addInputFile("rosenbrock_ref.dat")
mycode.addInputFile("rosenbrock_multi.C")

# Definition of the reference dataserver
tdsref = DataServer.TDataServer("tdsref", "Objectives values")
tdsref.fileDataRead("rosenbrock_ref.dat")

# Definition of the optimizer
topt = Optimizer.TOptimizer(tds, mycode)
topt.addObjective("obj1", tdsref, "y", fout, "yhat")
topt.optimize()

c = ROOT.TCanvas()
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
tds.draw("b:a", "", "lp")

Creation of the dataserver that will store the searched parameters values, and addition of the attributes a and b that will be read in the input file "input_rosenbrock_with_keys.dat". Note that these definitions introduce the domains of research of a and b as the interval [0 ; 5], the start values as 1. for a and 2. for b, and the step value as 0.1.

# Definition of the dataserver
tds = DataServer.TDataServer();

Definition of the output file of the code, "_rosenbrock_multi_.dat" (generated by the macro rosenbrock_multi.C), and definition of the output attribute, "yhat":

# Definition of the output file of the code 
fout = Launcher.TOutputFileRow("_rosenbrock_multi_.dat");
fout.addAttribute(DataServer.TAttribute("yhat"), 3);

Definition of the code to run (the root command), its output file, and the files it needs to be able and run the computation. Note that ROOT is run with options "-l" not to display splash screen, and "-q" to exit after execution (otherwise the macro execution would fail):

# Definition of the code  
mycode = Launcher.TCode(tds, "root -l -q rosenbrock_multi.C >> /dev/null");
mycode.addOutputFile(fout);
mycode.addInputFile("rootlogon.py");
mycode.addInputFile("rosenbrock_ref.dat");
mycode.addInputFile("rosenbrock_multi.C");

Creation of the dataserver tdsref for the reference values, and importation of these values:

# Definition of the reference dataserver    
tdsref = DataServer.TDataServer("tdsref", "Objectives values");
tdsref.fileDataRead("rosenbrock_ref.dat");

Definition of the optimizer object, addition of an objective from the "y" attribute of tdsref and the "yhat" attribute read from the file fout, and run of the optimisation process:

# Definition of the optimizer 
topt = Optimizer.TOptimizer(tds, mycode);
topt.addObjective("obj1", tdsref, "y", fout, "yhat");
topt.optimize();

Plot of the evolution of searched parameters a and b throw iterations:

c=ROOT.TCanvas();
tds.draw("b:a","","lp");

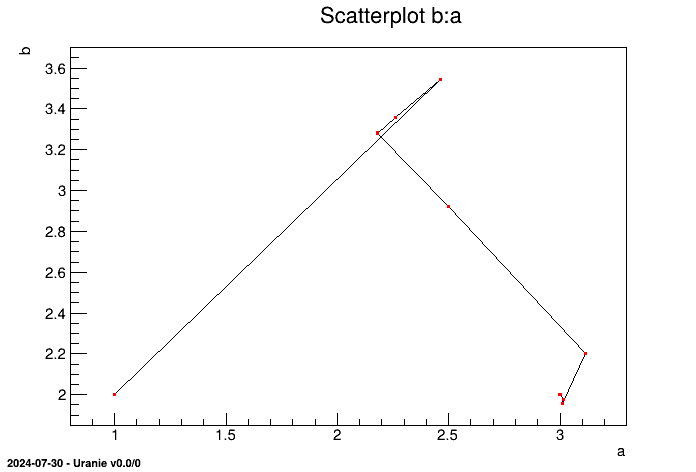
We can see in the graphic below that the parameters a and b converge from the point (1.;2.) to the point (3.;2.), where the values used to generate the data stored in the rosenbrock_ref.dat file.

Figure XIV.81. Evolution of searched parameters a and b throw iterations

Processing optimizeRosenbrockMulti.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024



 ** addObjective ystar(y) in TDS (tdsref) yhat(yhat) in the output file(_rosenbrock_multi_.dat)
 **   sLibraryName[Minuit2]
 **    sMethodName[Migrad]
 ** Problem[kSumOfSquare]
 ** _ninput [ 2]
 ** _noutput [ 1]
 ** Attribute[yhat]-- Del
 ** Attribute[b]
 ** Attribute[a]
 ** indx[0] Name[obj1]
 ** list of Objectives size(1) _dSumOfWeight(0)
 ** Objective i[0/1] Name[obj1] weight( 1)
 ** End Of list of Objectives _dSumOfWeight[1]
 ** _sCriteria [ obj1]

*************************************
 *** TMultiGenSumOfSquares::init
 *** TMultiGenSumOfSquares::clean
 *** End Of TMultiGenSumOfSquares::init
*************************************
 ** _sCost[obj1]
 ********** Print state [0] option[Init]
 **   name [ a] Origin[kAttribute] Value[1]
 **   name [ b] Origin[kAttribute] Value[2]
 **   name [ obj1] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [53] option[Final]
 **   name [ a] Origin[kAttribute] Value[2.99971]
 **   name [ b] Origin[kAttribute] Value[1.99974]
 **   name [ obj1] Origin[kAttribute] Value[3.69704e-06]
 ********** End Of Print state [53]

If we consider now that the external code (the Root macro in our case) cannot return the computed values anymore, but only an error (the quadratic error in our case) between the reference values and the estimated values on the reference TDataServer, we are back in the function optimisation situation, where the function to minimise is the error function, and its input parameters the parameters of the function.

To get such a case, we just modify the rosenbrock_multi.C macro to become the rosenbrock_error.C as discussed in the C++ version of this manual.

We can now use this macro as an external code we want to minimise the output:

"""
Example of code optimisation with errors
"""
from rootlogon import ROOT, DataServer, Launcher, Optimizer


# Definition of the dataserver
tds = DataServer.TDataServer()

# Definition of the attributes
sJDDReference = "input_rosenbrock_with_keys.dat"
tds.addAttribute(DataServer.TAttribute("a", 0.0, 5.0))
tds.getAttribute("a").setFileKey(sJDDReference, "a")
tds.getAttribute("a").setDefaultValue(1.0)
tds.getAttribute("a").setStepValue(0.1)
tds.addAttribute(DataServer.TAttribute("b", 0.0, 5.0))
tds.getAttribute("b").setFileKey(sJDDReference, "b")
tds.getAttribute("b").setDefaultValue(2.0)
tds.getAttribute("b").setStepValue(0.1)

# Definition of the output file of the code
fout = Launcher.TOutputFileKey("_rosenbrock_error_.dat")
fout.addAttribute(DataServer.TAttribute("normL2"))

# Definition of the code
to_null = " > NUL" if ROOT.gSystem.GetBuildArch() == "win64" else " >> /dev/null"
mycode = Launcher.TCode(tds, "root -b -l -q rosenbrock_error.C" + to_null)
mycode.addOutputFile(fout)
mycode.addInputFile("rootlogon.C")
mycode.addInputFile("rosenbrock_ref.dat")
mycode.addInputFile("rosenbrock_error.C")

# Definition of the optimizer
topt = Optimizer.TOptimizer(tds, mycode)
topt.setTolerance(1e-5)
topt.optimize()

c = ROOT.TCanvas()
pad = ROOT.TPad("pad", "pad", 0, 0.03, 1, 1)
pad.Draw()
tds.draw("b:a", "", "lp")

Creation of the dataserver that will store the searched parameters values, and addition of the attributes a and b that will be read in the input file "input_rosenbrock_with_keys.dat".

# Definition of the dataserver
tds = DataServer.TDataServer();

# Definition of the attributes
TString sJDDReference = "input_rosenbrock_with_keys.dat"

Definition of the output file of the code, "_rosenbrock_error_.dat" (generated by the macro rosenbrock_error.C), and definition of the output attribute that will be got them from this file, "normL2";

# Definition of the output file of the code
fout = Launcher.TOutputFileKey("_rosenbrock_error_.dat");
fout.addAttribute(DataServer.TAttribute("normL2"));

Definition of the code to run (the root command), its output file, and the files it needs to be able to run the computation. Note that ROOT is run with options "-l" not to display splash screen, and "-q" to exit after execution (otherwise the macro execution would fail).

# Definition of the code
mycode = Launcher.TCode(tds, "root -l -q rosenbrock_error.py >> /dev/null");

Definition of the optimizer object, setting of the tolerance to 1e-5, and run of the optimisation process:

# Definition of the optimizer
topt = Optimizer.TOptimizer(tds, mycode);
topt.setTolerance(1e-5);
topt.optimize();

The remaining lines are dealing with the plotting of the evolution of searched parameters a and b throw iterations.

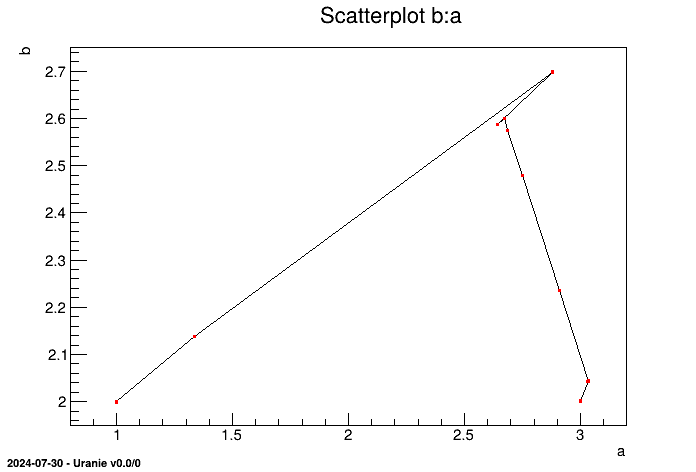
We can see in the graphic below that the parameters a and b converge from the point (1.;2.) to the point (3.;2.), where the values used to generate the data stored in the rosenbrock_ref.dat file.

Figure XIV.82. Evolution of searched parameters a and b throw iterations

Processing optimizeRosenbrockError.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

 **   sLibraryName[Minuit2]
 **    sMethodName[Migrad]
 ** Problem[kMinimizeCode]
 ** input :: ivar[0/3] name[a]
 ** input :: ivar[1/3] name[b]
 ** output :: ivar[2/3] name[normL2]
 ** TMultiGenCode::init _sCost[normL2] _nCost[ 1]
 ** _sCost[normL2]
 ********** Print state [0] option[Init]
 **   name [ a] Origin[kAttribute] Value[1]
 **   name [ b] Origin[kAttribute] Value[2]
 **   name [ normL2] Origin[kAttribute] Value[1.23457]
 ********** End Of Print state [0]
 <URANIE::INFO> 
 <URANIE::INFO> *** URANIE INFORMATION ***
 <URANIE::INFO> *** File[${SOURCEDIR}/launCHER/souRCE/TCode.cxx] Line[721]
 <URANIE::INFO> TCode::init Method
 <URANIE::INFO>  The launching directory "${RUNNINGDIR}/URANIE/UranieLauncher_1" does not exist
 <URANIE::INFO>  URANIE creates it for you
 <URANIE::INFO> *** END of URANIE INFORMATION ***
 <URANIE::INFO> 
 ********** Print state [68] option[Final]
 **   name [ a] Origin[kAttribute] Value[3]
 **   name [ b] Origin[kAttribute] Value[2.00001]
 **   name [ normL2] Origin[kAttribute] Value[2.75242e-10]
 ********** End Of Print state [68]