Documentation / User's manual in Python :

The objective of the macro is to optimize the section of the hollow bar defined in Section IX.2.2 using the NLopt solvers (reducing it to a single-criterion optimisation as already explained in Section IX.3. This can be done with different solvers, the results being achieved within more or less time and following the requested constraints with more or less accuracy (depending on the hypothesis embedded by the chosen solver).

"""
Example of hollow bar optimisation
"""
import numpy as np
from rootlogon import DataServer, Relauncher, Reoptimizer

# variables
x = DataServer.TAttribute("x", 0.0, 1.0)
y = DataServer.TAttribute("y", 0.0, 1.0)
thick = DataServer.TAttribute("thick")  # thickness
sect = DataServer.TAttribute("sect")  # section of the pipe
dist = DataServer.TAttribute("dist")  # distortion

# Creating the TCodeEval, dumping output of the dummy python in output file
python_exec = "python3"
if ROOT.gSystem.GetBuildArch() == "win64":
    python_exec = python_exec[:-1]
code = Relauncher.TCodeEval(python_exec + " bar.py > bartoto.dat")

# Pass the python script itself as input. inputs are modified in bar.py
inputfile = Relauncher.TKeyScript("bar.py")
inputfile.addInput(x, "x")
inputfile.addInput(y, "y")
code.addInputFile(inputfile)

# precise the name of the output file in which to read the three output
outputfile = Relauncher.TFlatResult("bartoto.dat")
outputfile.addOutput(thick)
outputfile.addOutput(sect)
outputfile.addOutput(dist)
code.addOutputFile(outputfile)

# Create a runner
runner = Relauncher.TSequentialRun(code)
runner.startSlave()  # Usual Relauncher construction

if runner.onMaster():

    # Create the TDS
    tds = DataServer.TDataServer("vizirDemo", "Param de l'opt vizir")
    tds.addAttribute(x)
    tds.addAttribute(y)

    # Choose a solver
    solv = Reoptimizer.TNloptCobyla()
    # solv = Reoptimizer.TNloptBobyqa()
    # solv = Reoptimizer.TNloptPraxis()
    # solv = Reoptimizer.TNloptNelderMead()
    # solv = Reoptimizer.TNloptSubplexe()

    # Create the single-objective constrained optimizer
    opt = Reoptimizer.TNlopt(tds, runner, solv)

    # add the objective
    opt.addObjective(sect)  # minimizing the section

    # and the constrains
    constrDist = Reoptimizer.TLesserFit(14)
    opt.addConstraint(dist, constrDist)  # distortion (dist < 14)
    positiv = Reoptimizer.TGreaterFit(0.4)
    opt.addConstraint(thick, positiv)  # thickness (thick > 0.4)

    # Starting point and maximum evaluation
    point = np.array([0.9, 0.2])
    opt.setStartingPoint(len(point), point)
    opt.setMaximumEval(1000)

    opt.solverLoop()  # running the optimization

    # Stop the slave processes
    runner.stopSlave()

# solution
tds.getTuple().Scan("*", "", "colsize=9 col=:::5:4")

The variables are defined as follow:

## variables
x=DataServer.TAttribute("x", 0.0, 1.0)
y=DataServer.TAttribute("y", 0.0, 1.0)
thick=DataServer.TAttribute("thick") # thickness
sect=DataServer.TAttribute("sect") # section of the pipe
dist=DataServer.TAttribute("dist"); # distortion

where the first two are the input ones while the last ones are computed using the provided code (as explained in Section IX.2.2). This code is configured through these lines:

# Creating the Launcher.TCodeEval, dumping output of the dummy python in an output file
code=Relauncher.TCodeEval("python bar.py > bartoto.dat");

# Pass the python script itself as a input file. x and y will be modified in bar.py directly
inputfile=Relauncher.TKeyScript("bar.py");
inputfile.addInput(x,"x");
inputfile.addInput(y,"y");
code.addInputFile(inputfile);

# precise the name of the output file in which to read the three output variables
outputfile=Relauncher.TFlatResult("bartoto.dat");
outputfile.addOutput(thick);
outputfile.addOutput(sect);
outputfile.addOutput(dist);
code.addOutputFile(outputfile);

# Create a runner
runner=Relauncher.TSequentialRun(code);
runner.startSlave(); # Usual Relauncher construction

The usual Relauncher construction is followed, using a TSequentialRun runner and the solver is chosen in these lines:

## Choose a solver 
solv=Reoptimizer.TNloptCobyla();
#solv=Reoptimizer.TNloptBobyqa()
#solv=Reoptimizer.TNloptPraxis()
#solv=Reoptimizer.TNloptNelderMead()
#solv=Reoptimizer.TNloptSubplexe()

Combining the runner, solver and dataserver, the master object is created and the objective and constraint are defined (keeping in mind that only single-criterion problems are implemented when dealing with NLopt, so the distortion criteria is downgraded to a constraint). This is done in

# Create the single-objective constrained optimizer
opt=Reoptimizer.TNlopt(tds, runner, solv);

# add the objective
opt.addObjective(sect); # minimizing the section

# and the constrains
constrDist=Reoptimizer.TLesserFit(14);
opt.addConstraint(dist,constrDist); # on the distortion (dist < 14)
positiv=Reoptimizer.TGreaterFit(0.4);
opt.addConstraint(thick,positiv); # and on the thickness (thick > 0.4)

Finally the starting point is set along with the maximal number of evaluation just before starting the loop.

## Starting point and maximum evaluation
point = array([0.9 , 0.2]);
opt.setStartingPoint(point);
opt.setMaximumEval(1000);
opt.solverLoop(); # running the optimization

This macro leads to the following result

Processing reoptimizeHollowBarCode.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

|....:....|....:....|....:....|....:....
|***************************************************************************
*    Row   * vizirDemo *       x.x *       y.y * thick * sect * dist.dist *
***************************************************************************
*        0 *         0 * 0.5173156 * 0.1173173 * 0.399 * 0.25 * 13.999986 *
***************************************************************************

The objective of the macro is to optimize the section of the hollow bar defined in Section IX.2.2 using the NLopt solvers (reducing it to a single-criterion optimisation as already explained in Section IX.3. It is largely based on the previous macro, the main change being the fact that we allow different starting points.

"""
Example of hollow bar optimisation in multistart mode
"""
import numpy as np
from rootlogon import DataServer, Relauncher, Reoptimizer

# variables
x = DataServer.TAttribute("x", 0.0, 1.0)
y = DataServer.TAttribute("y", 0.0, 1.0)
thick = DataServer.TAttribute("thick")  # thickness
sect = DataServer.TAttribute("sect")  # section of the pipe
dist = DataServer.TAttribute("dist")  # distortion

# Creating the TCodeEval, dumping output of the dummy python in an output file
python_exec = "python3"
if ROOT.gSystem.GetBuildArch() == "win64":
    python_exec = python_exec[:-1]
code = Relauncher.TCodeEval(python_exec + " bar.py > bartoto.dat")

# Pass the python script itself as input. inputs are modified in bar.py
inputfile = Relauncher.TKeyScript("bar.py")
inputfile.addInput(x, "x")
inputfile.addInput(y, "y")
code.addInputFile(inputfile)

# precise the name of the output file in which to read the three output
outputfile = Relauncher.TFlatResult("bartoto.dat")
outputfile.addOutput(thick)
outputfile.addOutput(sect)
outputfile.addOutput(dist)
code.addOutputFile(outputfile)

# Create a runner
runner = Relauncher.TSequentialRun(code)
runner.startSlave()  # Usual Relauncher construction

if runner.onMaster():

    # Create the TDS
    tds = DataServer.TDataServer("vizirDemo", "Param de l'opt vizir")
    tds.addAttribute(x)
    tds.addAttribute(y)

    # Choose a solver
    solv = Reoptimizer.TNloptCobyla()
    # solv = Reoptimizer.TNloptBobyqa()
    # solv = Reoptimizer.TNloptPraxis()
    # solv = Reoptimizer.TNloptNelderMead()
    # solv = Reoptimizer.TNloptSubplexe()

    # Create the single-objective constrained optimizer
    opt = Reoptimizer.TNlopt(tds, runner, solv)

    # add the objective
    opt.addObjective(sect)  # minimizing the section

    # and the constrains
    constrDist = Reoptimizer.TLesserFit(14)
    opt.addConstraint(dist, constrDist)  # distortion (dist < 14)
    positiv = Reoptimizer.TGreaterFit(0.4)
    opt.addConstraint(thick, positiv)  # thickness (thick > 0.4)

    # Starting point
    p1 = np.array([0.9, 0.2])
    p2 = np.array([0.7, 0.1])
    p3 = np.array([0.5, 0.4])
    opt.setStartingPoint(len(p1), p1)
    opt.setStartingPoint(len(p2), p2)
    opt.setStartingPoint(len(p3), p3)

    # Set maximum evaluation
    opt.setMaximumEval(1000)

    opt.solverLoop()  # running the optimization

    # Stop the slave processes
    runner.stopSlave()

# solution
tds.getTuple().Scan("*", "", "colsize=9 col=:::5:4")

As stated previously, the purpose of this macro is to use different starting points for optimisation fully based on the macro shown in Section XIV.10.1. The only difference is highlighted here:

# Starting point 
p1 = numpy.array([0.9 , 0.2]); p2 = numpy.array([0.7 , 0.1]); p3 = numpy.array([0.5 , 0.4]);
opt.setStartingPoint(len(p1),p1);
opt.setStartingPoint(len(p2),p2);
opt.setStartingPoint(len(p3),p3);

The results of this is that optimisation is performed three times, using the three starting points provided. Here it is done sequentially, but obviously, the main idea is that it is a convenient way to parallelise these optimisation. This could be done for instance, simply by changing the runner line from

runner=Relauncher.TSequentialRun(code);

to, for instance in our case with 3 starting points

runner=Relauncher.TThreadedRun(code,4);

This macro leads to the following result

Processing reoptimizeHollowBarCodeMS.py...

--- Uranie v0.0/0 --- Developed with ROOT (6.32.02)
                      Copyright (C) 2013-2024 CEA/DES 
                      Contact: support-uranie@cea.fr 
                      Date: Tue Jan 09, 2024

|....:....|....:....|....:....|....:....|....:....0050
|....:....|....:....
|....:....|....:....|....:....0100
|..
..:....|....:....|....:...
***************************************************************************
*    Row   * vizirDemo *       x.x *       y.y * thick * sect * dist.dist *
***************************************************************************
*        0 *         0 * 0.5173155 * 0.1173213 * 0.399 * 0.25 * 14.000005 *
*        1 *         1 * 0.5173156 * 0.1173173 * 0.399 * 0.25 * 13.999986 *
*        2 *         2 * 0.5173155 * 0.1173155 *   0.4 * 0.25 *        14 *
***************************************************************************

The objective of the macro is to optimize the section and distortion of the hollow bar defined in Section IX.2.2 using the evolutionary solvers. This can be done with different solvers, the one chosen here being the TVizirGenetic one.

"""
Example of hollow bar optimisation with Vizir
"""
from rootlogon import ROOT, DataServer, Relauncher, Reoptimizer

# variables
x = DataServer.TAttribute("x", 0.0, 1.0)
y = DataServer.TAttribute("y", 0.0, 1.0)
thick = DataServer.TAttribute("thick")  # thickness
sect = DataServer.TAttribute("sect")  # section of the pipe
dist = DataServer.TAttribute("dist")  # distortion

# Creating TCodeEval, dumping output in an output
python_exec = "python3"
if ROOT.gSystem.GetBuildArch() == "win64":
    python_exec = python_exec[:-1]
code = Relauncher.TCodeEval(python_exec + " bar.py > bartoto.dat")

# Pass the python script as a input. Inputs are modified in bar.py
inputfile = Relauncher.TKeyScript("bar.py")
inputfile.addInput(x, "x")
inputfile.addInput(y, "y")
code.addInputFile(inputfile)

# precise the output file in which to read the three outputs
outputfile = Relauncher.TFlatResult("bartoto.dat")
outputfile.addOutput(thick)
outputfile.addOutput(sect)
outputfile.addOutput(dist)
code.addOutputFile(outputfile)

# Create a runner
runner = Relauncher.TSequentialRun(code)
runner.startSlave()  # Usual Relauncher construction

if runner.onMaster():

    # Create the TDS
    tds = DataServer.TDataServer("vizirDemo", "Param de l'opt vizir")
    tds.addAttribute(x)
    tds.addAttribute(y)

    # create the vizir genetic solver
    solv = Reoptimizer.TVizirGenetic()
    # Size of the population and maximum number of evaluation
    solv.setSize(200, 15000)

    # Create the multi-objective constrained optimizer
    opt = Reoptimizer.TVizir2(tds, runner, solv)

    # add the objective
    opt.addObjective(sect)  # minimizing the section
    opt.addObjective(dist)  # minimizing the distortion

    # and the constrains
    positiv = Reoptimizer.TGreaterFit(0.4)
    opt.addConstraint(thick, positiv)  # on thickness (thick > 0.4)

    opt.solverLoop()  # running the optimization

    # Stop the slave processes
    runner.stopSlave()

fig1 = ROOT.TCanvas("fig1", "Pareto Zone", 5, 64, 1270, 667)
phi = 12
theta = 30
pad1 = ROOT.TPad("pad1", "", 0, 0.03, 1, 1)
pad2 = ROOT.TPad("pad2", "", 0, 0.03, 1, 1)
pad2.SetFillStyle(4000)  # will be transparent

pad1.Draw()
pad1.Divide(2, 1)
pad1.cd(1)
ROOT.gPad.SetPhi(phi)
ROOT.gPad.SetTheta(theta)

ROOT.gStyle.SetLabelSize(0.03)
ROOT.gStyle.SetLabelSize(0.03, "Y")
ROOT.gStyle.SetLabelSize(0.03, "Z")

tds.getTuple().Draw("sect:y:x")
# Get the TH3 to change Z axis color
htemp = ROOT.gPad.GetPrimitive("htemp")
htemp.SetTitle("")
htemp.GetZaxis().SetLabelColor(2)
htemp.GetZaxis().SetAxisColor(2)
htemp.GetZaxis().SetTitleColor(2)

fig1.cd()
pad2.Draw()
pad2.Divide(2, 1)
pad2.cd(1)
ROOT.gPad.SetFillStyle(4000)
ROOT.gPad.SetPhi(phi)
ROOT.gPad.SetTheta(theta)
tds.getTuple().SetMarkerColor(4)
tds.getTuple().Draw("dist:y:x")
htemp = ROOT.gPad.GetPrimitive("htemp")
htemp.SetTitle("")
htemp.GetZaxis().SetLabelColor(4)
htemp.GetZaxis().SetAxisColor(4)
htemp.GetZaxis().SetTitleColor(4)
htemp.GetZaxis().SetTickSize(-1*htemp.GetZaxis().GetTickLength())
htemp.GetZaxis().SetLabelOffset(-15*htemp.GetZaxis().GetLabelOffset())
htemp.GetZaxis().LabelsOption("d")
htemp.GetZaxis().SetTitleOffset(-1.5*htemp.GetZaxis().GetTitleOffset())
htemp.GetZaxis().RotateTitle()

pad2.cd(2)
tds.getTuple().SetMarkerColor(2)
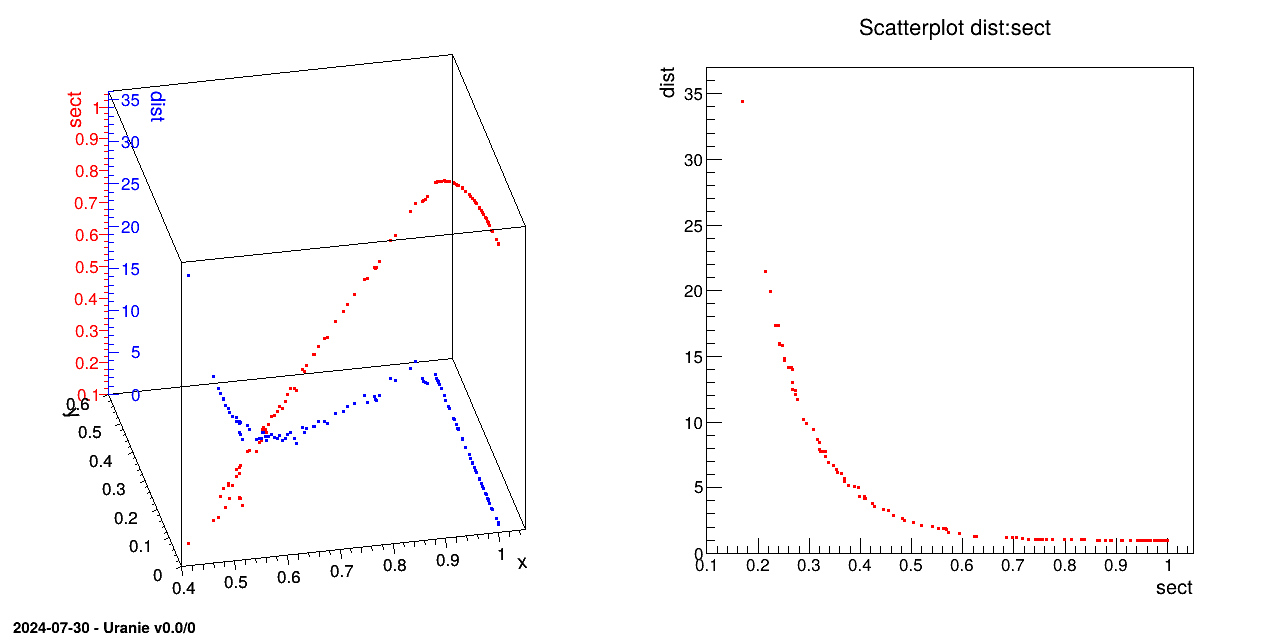
tds.draw("dist:sect")

The variables are defined as follow:

## variables
x=DataServer.TAttribute("x", 0.0, 1.0)
y=DataServer.TAttribute("y", 0.0, 1.0)
thick=DataServer.TAttribute("thick") # thickness
sect=DataServer.TAttribute("sect") # section of the pipe
dist=DataServer.TAttribute("dist"); # distortion

where the first two are the input ones while the last ones are computed using the provided code (as explained in Section IX.2.2). This code is configured through these lines

## Creating the TCodeEval, dumping output of the dummy python in an output file
code=Relauncher.TCodeEval("python bar.py > bartoto.dat");

# Pass the python script itself as a input file. x and y will be modified in bar.py directly
inputfile=Relauncher.TKeyScript("bar.py");
inputfile.addInput(x,"x");
inputfile.addInput(y,"y");
code.addInputFile(inputfile);

# precise the name of the output file in which to read the three output variables
outputfile=Relauncher.TFlatResult("bartoto.dat");
outputfile.addOutput(thick);
outputfile.addOutput(sect);
outputfile.addOutput(dist);
code.addOutputFile(outputfile);

The usual Relauncher construction is followed, using a TSequentialRun runner and the solver is chosen in these lines

## create the vizir genetic solver
solv=Reoptimizer.TVizirGenetic();
# Set the size of the population to 150, and a maximum number of evaluation at 15000
solv.setSize(200,15000); 

Combining the runner, solver and dataserver, the master object is created and the objective and constraint are defined. This is done in:

## Create the multi-objective constrained optimizer
opt=Reoptimizer.TVizir2(tds, runner, solv); 

# add the objective
opt.addObjective(sect); # minimizing the section
opt.addObjective(dist); # minimizing the distortion

# and the constrains
positiv=Reoptimizer.TGreaterFit(0.4);
opt.addConstraint(thick,positiv);  #on thickness (thick > 0.4)

Finally the optimisation is launched and the rest of code is providing the graphical result shown in next section.

The objective of the macro is to optimize the section and distortion of the hollow bar defined in Section IX.2.2 using the evolutionary solvers, with a reduce number of points to compose the Pareto set/front. This example is comparing both the usual Vizir genetic algorithm and the MOEAD implementation that is meant to be a many-objective criteria algorithm. A short discussion on the many-objective aspect can be found in [metho].

"""
Example of hollow bar optimisation with Moead approach
"""
from array import array
from rootlogon import ROOT, DataServer, Relauncher, Reoptimizer

# variables
x = DataServer.TAttribute("x", 0.0, 1.0)
y = DataServer.TAttribute("y", 0.0, 1.0)
thick = DataServer.TAttribute("thick")  # thickness
sect = DataServer.TAttribute("sect")  # section of the pipe
dist = DataServer.TAttribute("dist")  # distortion

ROOT.gROOT.LoadMacro("UserFunctions.C")

# Creating the assessor using the analytical function
code = Relauncher.TCIntEval("barAllCost")
code.addInput(x)
code.addInput(y)
code.addOutput(thick)
code.addOutput(sect)
code.addOutput(dist)

# Create a runner
runner = Relauncher.TSequentialRun(code)
runner.startSlave()  # Usual Relauncher construction

NB = 20
nMax = 3000
total = 4*NB
if runner.onMaster():
    # ==================================================
    # ========= Classical Vizir implementation =========
    # ==================================================

    # Create the TDS
    tds_viz = DataServer.TDataServer("vizirDemo", "Vizir parameter dataser")
    tds_viz.addAttribute(x)
    tds_viz.addAttribute(y)

    # create the vizir genetic solver
    solv_viz = Reoptimizer.TVizirGenetic()
    # Size of the population, and a maximum number of evaluation
    solv_viz.setSize(NB, nMax)

    # Create the multi-objective constrained optimizer
    opt_viz = Reoptimizer.TVizir2(tds_viz, runner, solv_viz)
    # add the objective
    opt_viz.addObjective(sect)  # minimizing the section
    opt_viz.addObjective(dist)  # minimizing the distortion

    # and the constrains
    positiv = Reoptimizer.TGreaterFit(0.4)
    opt_viz.addConstraint(thick, positiv)  # on thickness (thick > 0.4)

    opt_viz.solverLoop()  # running the optimization

    # ==================================================
    # ============== MOEAD implementation ==============
    # ==================================================

    # Create the TDS
    tds_moead = DataServer.TDataServer("vizirDemo", "Vizir parameter dataser")
    tds_moead.addAttribute(x)
    tds_moead.addAttribute(y)

    # create the vizir genetic solver
    solv_moead = Reoptimizer.TVizirGenetic()
    solv_moead.setMoeadDiversity(NB)
    solv_moead.setStoppingCriteria(1)
    solv_moead.setSize(0, nMax)

    # Create the multi-objective constrained optimizer
    opt_moead = Reoptimizer.TVizir2(tds_moead, runner, solv_moead)

    # add the objective
    opt_moead.addObjective(sect)  # minimizing the section
    opt_moead.addObjective(dist)  # minimizing the distortion

    opt_moead.addConstraint(thick, positiv)   # on thickness (thick > 0.4)

    opt_moead.solverLoop()  # running the optimization

    # Stop the slave processes
    runner.stopSlave()

    # Start the graphical part
    # Preparing canvas
    fig1 = ROOT.TCanvas("fig1", "Pareto Zone", 5, 64, 1270, 667)
    pad1 = ROOT.TPad("pad1", "", 0, 0.03, 1, 1)
    pad1.Draw()
    pad1.Divide(2, 1)
    pad1.cd(1)

    # extracting data to construct graphs
    viz = array('d', [0. for i in range(total)])
    # There is always one more point in moead
    moe = array('d', [0. for i in range(total+4)])
    tds_viz.getTuple().extractData(viz, total, "x:y:sect:dist", "", "column")
    tds_moead.getTuple().extractData(moe, total+4,
                                     "x:y:sect:dist", "", "column")

    set_viz = ROOT.TGraph(NB, array('d', [viz[i] for i in range(NB)]),
                          array('d', [viz[NB+i] for i in range(NB)]))
    fr_viz = ROOT.TGraph(NB, array('d', [viz[2*NB+i] for i in range(NB)]),
                         array('d', [viz[3*NB+i] for i in range(NB)]))
    set_viz.SetMarkerColor(4)
    set_viz.SetMarkerStyle(20)
    set_viz.SetMarkerSize(0.8)
    fr_viz.SetMarkerColor(4)
    fr_viz.SetMarkerStyle(20)
    fr_viz.SetMarkerSize(0.8)

    set_moe = ROOT.TGraph(NB+1, array('d', [moe[i] for i in range(NB+1)]),
                          array('d', [moe[NB+1+i] for i in range(NB+1)]))
    fr_moe = ROOT.TGraph(NB, array('d', [moe[2*(NB+1)+i] for i in range(NB+1)]),
                         array('d', [moe[3*(NB+1)+i] for i in range(NB+1)]))
    set_moe.SetMarkerColor(2)
    set_moe.SetMarkerStyle(20)
    set_moe.SetMarkerSize(0.8)
    fr_moe.SetMarkerColor(2)
    fr_moe.SetMarkerStyle(20)
    fr_moe.SetMarkerSize(0.8)

    # Legend
    ROOT.gStyle.SetLegendBorderSize(0)
    leg = ROOT.TLegend(0.25, 0.75, 0.55, 0.89)
    leg.AddEntry(set_viz, "Vizir algo", "p")
    leg.AddEntry(set_moe, "MOEAD algo", "p")

    # Pareto Set
    set_mg = ROOT.TMultiGraph()
    set_mg.Add(set_viz)
    set_mg.Add(set_moe)
    set_mg.Draw("aP")
    set_mg.SetTitle("Pareto Set")
    set_mg.GetXaxis().SetTitle("x")
    set_mg.GetYaxis().SetTitle("y")
    leg.Draw()
    ROOT.gPad.Update()

    # Pareto Front
    pad1.cd(2)
    fr_mg = ROOT.TMultiGraph()
    fr_mg.Add(fr_viz)
    fr_mg.Add(fr_moe)
    fr_mg.Draw("aP")
    fr_mg.SetTitle("Pareto front")
    fr_mg.GetXaxis().SetTitle("Section")
    fr_mg.GetYaxis().SetTitle("Distortion")
    leg.Draw()
    ROOT.gPad.Update()

The variables are defined as follow:

x=DataServer.TAttribute("x", 0.0, 1.0)
y=DataServer.TAttribute("y", 0.0, 1.0)
thick=DataServer.TAttribute("thick") # thickness
sect=DataServer.TAttribute("sect") # section of the pipe
dist=DataServer.TAttribute("dist"); # distortion

where the first two are the input ones while the last ones are computed using the provided code (as explained in Section IX.2.2). This code is configured through these lines

## Creating the assessor using the analytical function
code = Relauncher.TCIntEval("barAllCost");
code.addInput(x);
code.addInput(y);
code.addOutput(thick);
code.addOutput(sect);
code.addOutput(dist);

The usual Relauncher construction is followed, using a TSequentialRun runner. The first solver is defined in these lines

## create the vizir genetic solver
solv_viz = Reoptimizer.TVizirGenetic();
## Set the size of the population to 150, and a maximum number of evaluation at 15000
solv_viz.setSize(nbPoints,nMax); 

Combining the runner, solver and dataserver, the master object is created and the objective and constraint are defined. This is done in:

## Create the multi-objective constrained optimizer
opt_viz = Reoptimizer.TVizir2(tds_viz, runner, solv_viz); 
## add the objective
opt_viz.addObjective(sect); ## minimizing the section
opt_viz.addObjective(dist); ## minimizing the distortion
    
## and the constrains
positiv = Reoptimizer.TGreaterFit(0.4);
opt_viz.addConstraint(thick,positiv);  ##on thickness (thick > 0.4)

In a second block a new dataserver is created along with a new genetic solver in these lines:

## create the vizir genetic solver
solv_moead = Reoptimizer.TVizirGenetic();
solv_moead.setMoeadDiversity(nbPoints);
solv_moead.setStoppingCriteria(1);
solv_moead.setSize(0, nMax);

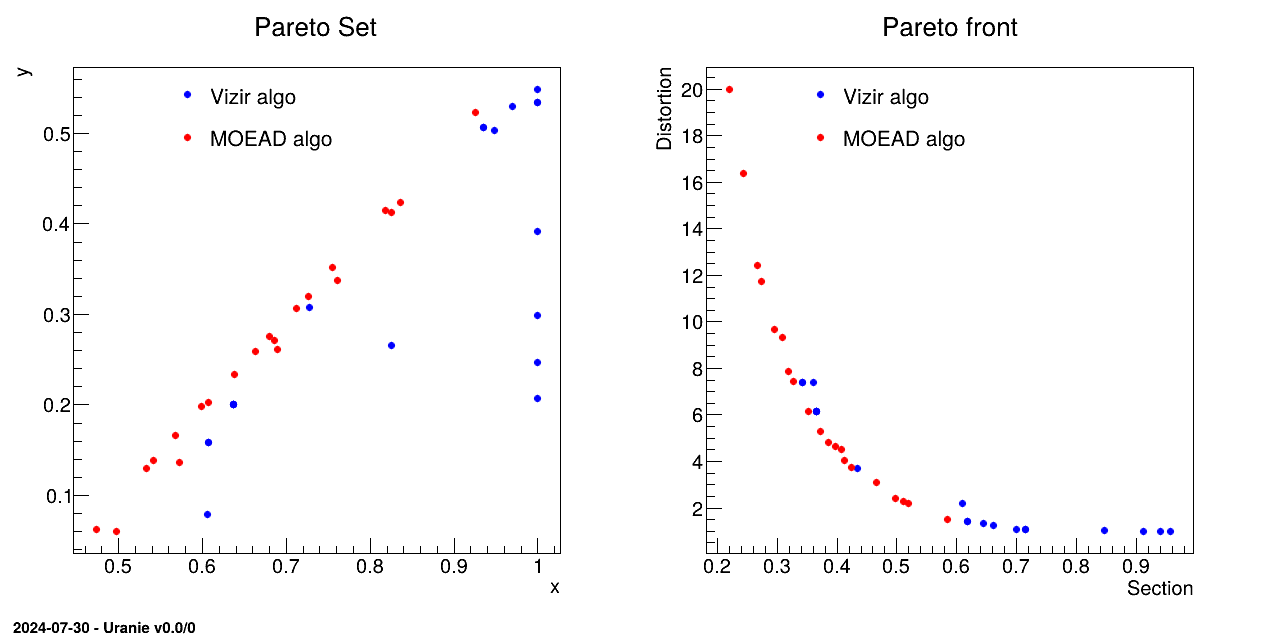
The idea here is to use the Moead algorithm whose principle in few words is to split the space into a certain numbers of direction intervals (set by the argument in the function setMoeadDiversity). This should provide a Pareto front with a better homogeneity in the front member distribution (particularly visible here when the size of the requested ensemble is small). The second method, setStoppingCriteria(1) states that the only stopping criteria available is the total number of estimation, allowed in the setSize method. Finally, the last function to be called is the setSize one, with a peculiar first argument here: the size of the pareto can be chosen but if 0 is put (as done here) the number of elements will be the number of intervals defined previously plus one (the plus one comes from the fact that the elements are created at the edge of every interval, so for 20 intervals, there are 21 edges in total).

The rest of the code is creating the plot shown below in which both Pareto set and front are compared.

The objective of the macro is to be able to run an evolutionary algorithm (here we are using a genetic one) with a limited number of code estimation and restart it from where it stopped if it has not converged the first time. This is of utmost usefulness when running a resource-consumming code or (/and) when running on a cluster with a limited number of cpu time. The classical hollow bar example defined in Section IX.2.2 is used to obtain a nice Pareto set/front.

"""
Example of hollow bar optimisation in split runs
"""
from rootlogon import ROOT, DataServer, Relauncher, Reoptimizer

TOLERANCE = 0.001
NBmaxEVAL = 1200
SIZE = 500


def launch_vizir(run_number, fig_one):
    """Factorised function to run the Vizir analaysis."""
    # variables
    xvar = DataServer.TAttribute("x", 0.0, 1.0)
    yvar = DataServer.TAttribute("y", 0.0, 1.0)
    thick = DataServer.TAttribute("thick")
    sect = DataServer.TAttribute("sect")
    defor = DataServer.TAttribute("defor")

    code = Relauncher.TCIntEval("barAllCost")
    code.addInput(xvar)
    code.addInput(yvar)
    code.addOutput(thick)
    code.addOutput(sect)
    code.addOutput(defor)

    # Create a runner
    runner = Relauncher.TSequentialRun(code)
    runner.startSlave()

    # Output to state whether convergence is reached
    has_converged = False
    if runner.onMaster():

        # Create the TDS
        tds = DataServer.TDataServer("vizirDemo", "Param de l'opt vizir")
        tds.addAttribute(xvar)
        tds.addAttribute(yvar)

        solv = Reoptimizer.TVizirGenetic()
        # Name of the file that will contain
        filename = "genetic.dump"
        # whether = Test if a genetic.dump exists. If not, it creates it
        # and returns false, so that the "else" part is done to start the
        # initialisation of the vizir algorithm.
        if solv.setResume(NBmaxEVAL, filename):
            print("Restarting Vizir")
        else:
            solv.setSize(SIZE, NBmaxEVAL)

        # Create the multi-objective constrained optimizer
        opt = Reoptimizer.TVizir2(tds, runner, solv)
        opt.setTolerance(TOLERANCE)
        # add the objective
        opt.addObjective(sect)
        opt.addObjective(defor)
        positiv = Reoptimizer.TGreaterFit(0.4)
        opt.addConstraint(thick, positiv)

        # resolution
        opt.solverLoop()
        has_converged = opt.isConverged()
        # Stop the slave processes
        runner.stopSlave()

        fig_one.cd(run_number+1)
        tds.getTuple().SetMarkerColor(2)
        tds.draw("defor:sect")
        tit = "Run number "+str(run_number+1)
        if has_converged:
            tit += ": Converged !"
        ROOT.gPad.GetPrimitive("__tdshisto__0").SetTitle(tit)

    return has_converged


ROOT.gROOT.LoadMacro("UserFunctions.C")
# Delete previous file if it exists
ROOT.gSystem.Unlink("genetic.dump")

finished = False
i = 0
fig1 = ROOT.TCanvas("fig1", "fig1", 1200, 800)
fig1.Divide(2, 2)
while not finished:
    finished = launch_vizir(i, fig1)
    i = i+1

The idea is to show how to run this kind of configuration: the function LaunchVizir is the usual script one can run to get an optimisation with Vizir on the hollow bar problem. The aim is to create a Pareto set of 500 points (SIZE) but only allowing 1200 estimation (NBmaxEVAL). With this configuration we are sure that a first round of estimation will not converge, so we will have to restart the optimisation from the point we stopped. With this regard, the beginning of this function is trivial and the main point to be discussed arises once the solver is created.

solv=Reoptimizer.TVizirGenetic();
## Name of the file that will contain
filename="genetic.dump";
## whether=Test a genetic.dump exists. If not, it creates it and returns false, so that
## the "else" part is done to start the initialisation of the vizir algorithm. 
if solv.setResume(NBmaxEVAL, filename) : print "Restarting Vizir";
else : solv.setSize(SIZE, NBmaxEVAL);    
          

Clearly here, the interesting part apart, from the definition of the name of the file in which the final state will be kept, is the first test on the solver, before using the setSize method. A new methods called setResume is called, with two arguments : the number of elements requested in the Pareto set and the name of the file in which to save the state or to restart from. This method returns "true" if genetic.dump is found and "false" if not. In the first case, the code will assume that this file is the result of a previous run and it will start the optimisation from the its content trying to get all the population non-dominated (if it's not yet the case). If, on the other hand, no file is found, then the code knows that it would have to store the results of its process, in a file whose name is the second argument, and because the function returns "false", then we move to the "else" part, that starts the optimisation.

Apart from this, the rest of the function is doing the optimisation, and plotting the pareto front in a provided canvas. The only new part here is the fact that the solver (its master in fact) is now able to tell whether it has converged or not through the following method

 hasConverged=opt.isConverged();

this argument being return as the results of the function.

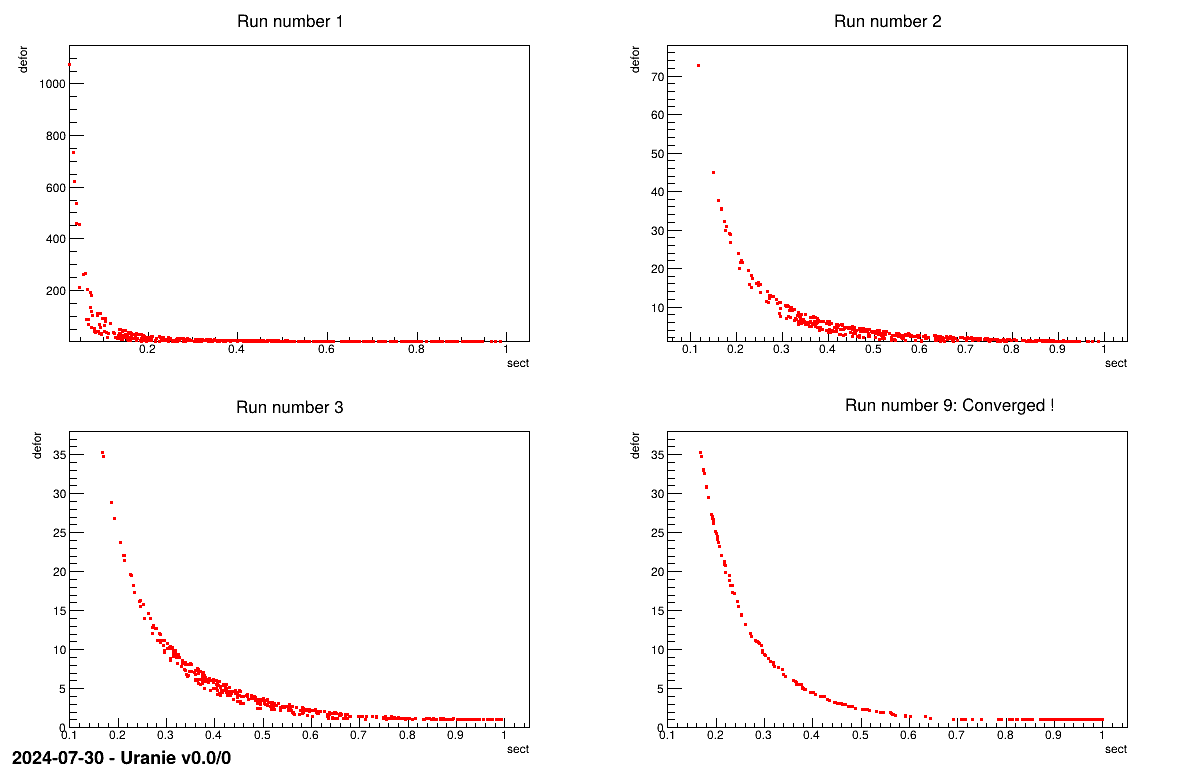
The rest of this macro plays the role of the user in front of a ROOT-console (its python interplay of course). It defines the correct namespace, loads the function file and destroys previously existing genetic.dump files. From there it runs the LaunchVizir function as many times as needed (thanks to the boolean returned) as the used would do, by restarting the macro, even after exiting the ROOT console.

The plot shown below represent the Pareto front every time the genetic algorithm stops (at the fourth run, it finally converges !).

The objective of the macro is to show an example of a two level parallelism program using the Mpi paradigm.

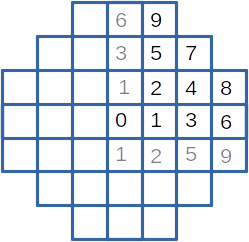
These example is inspired from a zoning problem of a small plant core with square assemblies. However, the physics embeded in it is reduced to none (sorry), and the problem is simplified. With symetries, the core is defined by 10 different assemblies presented on the following figure. For production purpose, only 5 assembly types are allowed, defined by an emission value.

Figure XIV.95. The core and its assemblies

To simplify the problem, some constraints are put :

For each assembly, a reception value is defined depending on the emission from itself and its neighbour's (just 8 neightbours are taken in account, the 4 nearest neighbours and 4 secondary neighbours). The global objective is to minimize the difference between the biggest and the smallest reception value.

Optimisation works on 4 emission values (the fifth value, affected to the external zone, is set, and all values are normalized with the total emission value) and each evaluation loops over the 35 possible arrangements (choose 3 zones from 7). A single evaluation take emission values and the selected zones and return the maximum reception difference.

This macro is splited in 2 files : the first one defines the low level evaluation function and is reused in the next reoptimizer example. It is quite a mock function, and is given to be complete, but is not needed to understand how to implement the two level MPI parallelism

#!/usr/bin/env python


# the different zones
# 
# 6 9
# 3 5 7
# 1 2 4 8
# 0 1 3 6
# 1 2 5 9

# 4 primary neighbours of a zone
near1 = [
    [1, 1, 1, 1],  # 0
    [0, 2, 2, 3],
    [1, 1, 4, 5],
    [1, 4, 5, 6],  # 3
    [2, 3, 7, 8],
    [2, 3, 7, 9],
    [3, 8, 9, 10],  # 6
    [4, 5, 10, 10],
    [4, 6, 10, 10],
    [5, 6, 10, 10]  # 9
]
# 4 secondary neighbours
near2 = [
    [2, 2, 2, 2],  # 0
    [1, 1, 4, 5],
    [0, 3, 3, 7],
    [2, 2, 8, 9],  # 3
    [1, 5, 6, 10],
    [1, 4, 6, 10],
    [4, 5, 10, 10],  # 6
    [2, 8, 9, 10],
    [3, 7, 10, 10],
    [3, 7, 10, 10]  # 9
]

# low level evaluation
def lowfun(edft, e_1, e_2, e_3, a_1, a_2, a_3):
    """ evaluate a zoning """
    def fill(loc, vid, val):
        """ fill a zone with an emission value """
        l_id = int(vid)
        loc[l_id] = val
        if l_id == 4:
            loc[5] = val

    def reception(loc, l_id):
        """ calculate reception in a zone """
        ret = loc[l_id]
        for l_iter in near1[l_id]:
            ret += loc[l_iter] / 8
        for l_iter in near2[l_id]:
            ret += loc[l_iter]/16
        return ret

    # init dft
    loc = [edft for i in range(11)]
    loc[8] = 0.8
    loc[9] = 0.8
    loc[10] = 0.0
    # init spec
    fill(loc, a_1, e_1)
    fill(loc, a_2, e_2)
    fill(loc, a_3, e_3)
    # normalize
    loc_all = loc[0] / 4
    for i in loc[1:]:
        loc_all += i
    locn = [i*10/loc_all for i in loc]

    # max diff
    loc_max = reception(locn, 0)
    loc_min = loc_max
    for i_id in range(1, 10):
        next_var = reception(locn, i_id)
        if next_var < loc_min:
            loc_min = next_var
        elif next_var > loc_max:
            loc_max = next_var
    # output
    ret = [loc_max - loc_min]
    for i in locn[:-1]:
        ret.append(i)
    return ret

The lowfun function deals, as expected, with the low level evaluation. In inputs it has the 4 emission values (default, zone1, zone2, zone3) and 3 indicators defining the zone affected by the extra emission value. It returns the maximal difference between two zone reception values and the 9 normalized emission values (informative data). Two arrays are used to define the neighbourhood

With the second file, the two level MPI parallelism is defined.

#!/usr/bin/env python

import ROOT
import URANIE.DataServer as DataServer
import URANIE.Relauncher as Relauncher
import URANIE.Reoptimizer as Reoptimizer
import URANIE.MpiRelauncher as MpiRelauncher

from reoptimizeZoneCore import lowfun

# resume from tds
def tds_resume(tds, attr):
    """ get the best zoning from tds """
    def get_in_tds(tds, leaf, l_id):
        """ get a zoning objective """
        tds.GetTuple().GetEntry(l_id)
        return leaf.GetValue(0)

    siz = tds.GetTuple().GetEntries()
    leaves = [tds.GetTuple().GetLeaf(a.GetName()) for a in attr]

    # search min
    k = 0
    loc_min = get_in_tds(tds, leaves[0], 0)
    for i in range(1, siz):
        cur = get_in_tds(tds, leaves[0], i)
        if (cur < loc_min):
            loc_min = cur
            k = i
    # all results
    tds.GetTuple().GetEntry(k)
    return [l.GetValue(0) for l in leaves]


# top level evaluation
def doefun(edft, ezon1, ezon2, ezon3) :
    """ find the best zoning for a given emission values """
    # inputs
    azon0 = DataServer.TAttribute("zon0", 0., 1.)
    azon1 = DataServer.TAttribute("zon1", 0., 1.)
    azon2 = DataServer.TAttribute("zon2", 0., 1.)
    azon3 = DataServer.TAttribute("zon3", 0., 1.)
    adef1 = DataServer.TAttribute("a1")
    adef2 = DataServer.TAttribute("a2")
    adef3 = DataServer.TAttribute("a3")
    funi = [azon0, azon1, azon2, azon3, adef1, adef2, adef3]
    # outputs
    namo = ["diff", "v0", "v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9"]
    funo = [DataServer.TAttribute(n) for n in namo]
    # low fun
    fun = Relauncher.TPythonEval(lowfun)
    for inp in funi:
        fun.addInput(inp)
    for out in funo:
        fun.addOutput(out)
    # runner
    # run = Relauncher.TSequentialRun(fun)
    run = MpiRelauncher.TSubMpiRun(fun)
    run.startSlave()
    if run.onMaster():
        # doe def
        data = DataServer.TDataServer("doe", "tds4doe")
        data.keepFinalTuple(False)
        for i in funi[4:7]:
            data.addAttribute(i)
        data.fileDataRead("reoptimizeZoneDoe.dat", False, True, "quiet")
        # realize doe
        launch = Relauncher.TLauncher2(data, run)
        launch.addConstantValue(azon0, edft)
        launch.addConstantValue(azon1, ezon1)
        launch.addConstantValue(azon2, ezon2)
        launch.addConstantValue(azon3, ezon3)
        launch.solverLoop()
        # get objective
        ret = tds_resume(data, funo)
        # clean
        run.stopSlave()
        ROOT.SetOwnership(run, True)
        return ret
    else:
        # return something to avoid warning
        # output number should be coherent
        return [0. for i in namo]


# top level control
def coeurR():
    """ optimization on emission values """
    # inputs
    nami = ["zone1", "zone2", "zone3", "zone4"]
    funi = [DataServer.TAttribute(n, 0., 1.) for n in nami]
    # outputs
    namo = ["diff", "v0", "v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9"]
    funo = [DataServer.TAttribute(n) for n in namo]
    # top fun
    fun = Relauncher.TPythonEval(doefun)
    for inp in funi:
        fun.addInput(inp)
    for out in funo:
        fun.addOutput(out)
    # runner
    # run = Relauncher.TSequentialRun(fun)
    run = MpiRelauncher.TBiMpiRun(fun, 3)
    run.startSlave()
    if run.onMaster():
        # data
        data = DataServer.TDataServer("tdsvzr", "tds4optim")
        fun.addAllInputs(data)
        # optim
        gen = Reoptimizer.TVizirGenetic()
        gen.setSize(300, 200000, 100)
        viz = Reoptimizer.TVizir2(data, run, gen)
        viz.addObjective(funo[0])
        viz.solverLoop()
        # results
        data.exportData("__coeurPy__.dat")
        # clean
        run.stopSlave()
        ROOT.SetOwnership(run, True)


#ROOT.EnableThreadSafety()
coeurR()

This script is structured with 3 functions :

TBiMpiRun and TSubMpiRun are used to allocate cpus between intermediate and low level. TBiMpiRun is used in reoptimizeZoningBiSubMpi (top) with an integer argument specifying the number of CPUs dedicated to each intermediate level. In our case (3), with 16 resources request to MPI, they are divided in 5 groups of 3 CPUs, and one CPU is left for the top level master (take care that the number of CPUs requested matches group size (16 % 3 == 1)). The top level Master sees 5 resources for his evaluations. TSubMpiRun is used in doefun function and gives access to the 3 own resources reserved in top level function.

Running the script is done as usual with MPI :

mpirun -n 16 python reoptimizeZoningBiSubMpi.py

At the begining of reoptimizeZoningBiSubMpi function there is a call to ROOT::EnableThreadSafety. It is unusefull in this case, but if we parallelize with threads instead of MPI. If you want to use both threads and MPI, it is recommended to use MPI at top level.

The objective of the macro is to give another example of a two level parallelism program using MPI paradigm. In the former example MPI function call is implicit using Uranie facilities. In this one, explicit calls to MPI functions is done. It's presented to illustrate the case when the user evaluation fonction is an MPI function.

It takes the former example of zoning problem and adapts it. The intermediate level does not use a TLauncher2 to run all different arrangements, but encodes it. Each Mpi ressources evaluates different possible arrangements keeping its best one, and Mpi reduce these results to the final result.

The low level evaluation function is the same than in previous example and is not shown again.

#!/usr/bin/env python

import ROOT
import URANIE.DataServer as DataServer
import URANIE.Relauncher as Relauncher
import URANIE.Reoptimizer as Reoptimizer
import URANIE.MpiRelauncher as MpiRelauncher

from mpi4py import MPI
import ctypes

from reoptimizeZoneCore import lowfun

# mpi4py helpers
def getCalculMpiComm() :
    """ convert C MPI_Comm to python """
    typemap = {
        ctypes.sizeof(ctypes.c_int) : ctypes.c_int, #mpich
        ctypes.sizeof(ctypes.c_void_p) : ctypes.c_void_p, #openmpi
    }
    comm = MPI.Comm()
    handle_t = typemap[MPI._sizeof(comm)]
    handle_new = handle_t.from_address(MPI._addressof(comm))
    handle_new.value = MpiRelauncher.TBiMpiRun.getCalculMpiCommPy()
    return comm


# doe
doe = [
    [0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 6], [4, 6, 7], [0, 6, 7], [0, 1, 7], # 7
    [0, 1, 3], [1, 2, 4], [2, 3, 6], [3, 4, 7], [0, 4, 6], [1, 6, 7], [0, 2, 7], # 14
    [0, 1, 4], [1, 2, 6], [2, 3, 7], [0, 3, 4], [1, 4, 6], [2, 6, 7], [0, 3, 7], # 21
    [0, 1, 6], [1, 2, 7], [0, 2, 3], [1, 3, 4], [2, 4, 6], [3, 6, 7], [0, 4, 7], # 28
    [0, 2, 4], [1, 3, 6], [2, 4, 7], [0, 3, 6], [1, 4, 7], [0, 2, 6], [1, 3, 7], # 35
]

# doe fun
def doefun(emz0, emz1, emz2, emz3) :
    """ find the best zoning for a given emission values """
    # mpi context
    comm = getCalculMpiComm()
    rank = comm.Get_rank()
    size = comm.Get_size()
    # search local best
    ind = rank
    idz1 = doe[ind][0]
    idz2 = doe[ind][1]
    idz3 = doe[ind][2]
    memo = lowfun(emz0, emz1, emz2, emz3, idz1, idz2, idz3)
    for next in range(rank, len(doe), size) :
        idz1 = doe[next][0]
        idz2 = doe[next][1]
        idz3 = doe[next][2]
        curr = lowfun(emz0, emz1, emz2, emz3, idz1, idz2, idz3)
        if curr[0] < memo[0] :
            memo = curr
    # global best
    # where is min
    ret = (memo[0], rank)
    (val, fid) = comm.allreduce(ret, op=MPI.MINLOC)
    # get all min value
    rval = memo
    if fid != 0 :
        if rank == fid :
            comm.send(memo, dest=0, tag=0)
        elif rank == 0 :
            rval = comm.recv(source=fid, tag=0)
    return rval

# top level control
def coeurMpi():
    """ optimization on emission values """
    # inputs
    nami = ["zone1", "zone2", "zone3", "zone4"]
    funi = [DataServer.TAttribute(n, 0., 1.) for n in nami]
    # outputs
    namo = ["diff", "v0", "v1", "v2", "v3", "v4", "v5", "v6", "v7", "v8", "v9"]
    funo = [DataServer.TAttribute(n) for n in namo]
    # top fun
    fun = Relauncher.TPythonEval(doefun)
    for inp in funi:
        fun.addInput(inp)
    for out in funo:
        fun.addOutput(out)
    # runner
    # run = Relauncher.TSequentialRun(fun)
    run = MpiRelauncher.TBiMpiRun(fun, 3, False)
    run.startSlave()
    if run.onMaster():
        # data
        data = DataServer.TDataServer("tdsvzr", "tds4optim")
        fun.addAllInputs(data)
        # optim
        gen = Reoptimizer.TVizirGenetic()
        gen.setSize(300, 200000, 100)
        viz = Reoptimizer.TVizir2(data, run, gen)
        viz.addObjective(funo[0])
        viz.solverLoop()
        # results
        data.exportData("__coeurMpy__.dat")
        # clean
        run.stopSlave()
        #ROOT.SetOwnership(run, True)


#ROOT.EnableThreadSafety()
coeurMpi()

The top level function (coeurMpi) does not change from the previous example. The only difference is in the creation of the TBiMpiRun instances, which is done with an extra parameter set to False. This tell the constructor to avoid calling MPI_Init function. With mpi4py, this call is already done when the module is imported

The evaluation MPI fonction (doefun) is totaly different. It uses the function getCalculMpiComm to get the MPI Communicator object (MPI.Comm) dedicated to the calcul ressources. With it, different call to its method can be done : Get_rank and Get_size to get the context ; allreduce, send and recv to communicate between calculs ressources.

Function getCalculMpiComm is an helper function use to convert the MPI communicator get from Uranie MpiRelauncher.TBiMpiRun.getCalculMpiCommPy class method to the mpi4py equivalent object

You may run this script the same way as the precedent example, with the same constraint on the ressource number. Also note that this version is really faster than the previous one, avoiding creation and manipulation of many TDataServer.