Documentation
/ Manuel utilisateur en Python
: 
This section introduces few examples dealing with calibration in order to illustrate the different techniques introduced in Chapter XI and few of the options available as well.
The purpose here is to calibrate the value of 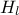 that entered the
that entered the flowrate model, when only two inputs have been varied
(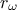 and
and
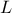 ) while the rest of the
variables are set to a frozen value:
) while the rest of the
variables are set to a frozen value: 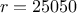 ,
, 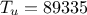 ,
, 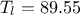 ,
, 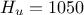 ,
, 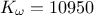 . The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the
. The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the TDataServer
objects). This macro shows how to use simple minimisation technique, with a Relauncher-architecture.
"""
Example of calibration using minimisation approach on flowrate 1D
"""
from rootlogon import ROOT, DataServer, Relauncher, Reoptimizer, Calibration
# Load the function flowrateCalib1D
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file
ExpData = "Ex2DoE_n100_sd1.75.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
# define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "pouet")
tdsPar.addAttribute(DataServer.TAttribute("hl", 700.0, 760.0))
tdsPar.getAttribute("hl").setDefaultValue(728.0)
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib1D")
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner = Relauncher.TSequentialRun(Model)
# Set the calibration object
cal = Calibration.TMinimisation(tdsPar, runner, 1)
cal.setDistanceAndReference("LS", tdsRef, "rw:l", "Qexp")
solv = Reoptimizer.TNloptSubplexe()
cal.setOptimProperties(solv)
cal.estimateParameters()
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
Apart from the first lines discussed in Section XI.2.4, the important line is the
one defining the starting point of the minimisation. This can be done by calling the
setStartingPoint method of the TNlopt class, or simply by defining
default value for the parameter attributes. This is done here:
tdsPar.getAttribute("hl").setDefaultValue(728.0)
This macro continues by defining the model and the way to run it. The instance created here, is a
TCIntEval which simply request the three input variables discussed above in the correct order. Here the first one has to be 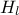 , the parameter that we want to calibrate, because of the way the
C++-function has been defined and then the two varying ones, (
, the parameter that we want to calibrate, because of the way the
C++-function has been defined and then the two varying ones, (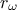 and
and 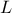 ) whose values are coming from the reference input file. Once done, the output
attribute is added (as our model computes only one variable) and the chosen distribution strategy is chosen to be
sequential.
) whose values are coming from the reference input file. Once done, the output
attribute is added (as our model computes only one variable) and the chosen distribution strategy is chosen to be
sequential.
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib1D")
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner=Relauncher.TSequentialRun(Model)
Once done the calibration object (TMinimisation) is created and, as discussed in Section XI.2.2.1, the first object to be created is the distance function (here the
least-square one) through the setDistanceAndReference, that also defines the TDataServer that
contains reference data, the name of the reference inputs and the reference variable to which the output of the
model should be compared with. Finally the optimisation algorithm is defined by creating an instance of
TNloptSubplexe and then the parameters are estimated.
# Set the calibration object
cal = Calibration.TMinimisation(tdsPar,runner,1)
cal.setDistanceAndReference("LS",tdsRef,"rw:l","Qexp")
solv=Reoptimizer.TNloptSubplexe()
cal.setOptimProperties(solv)
cal.estimateParameters()
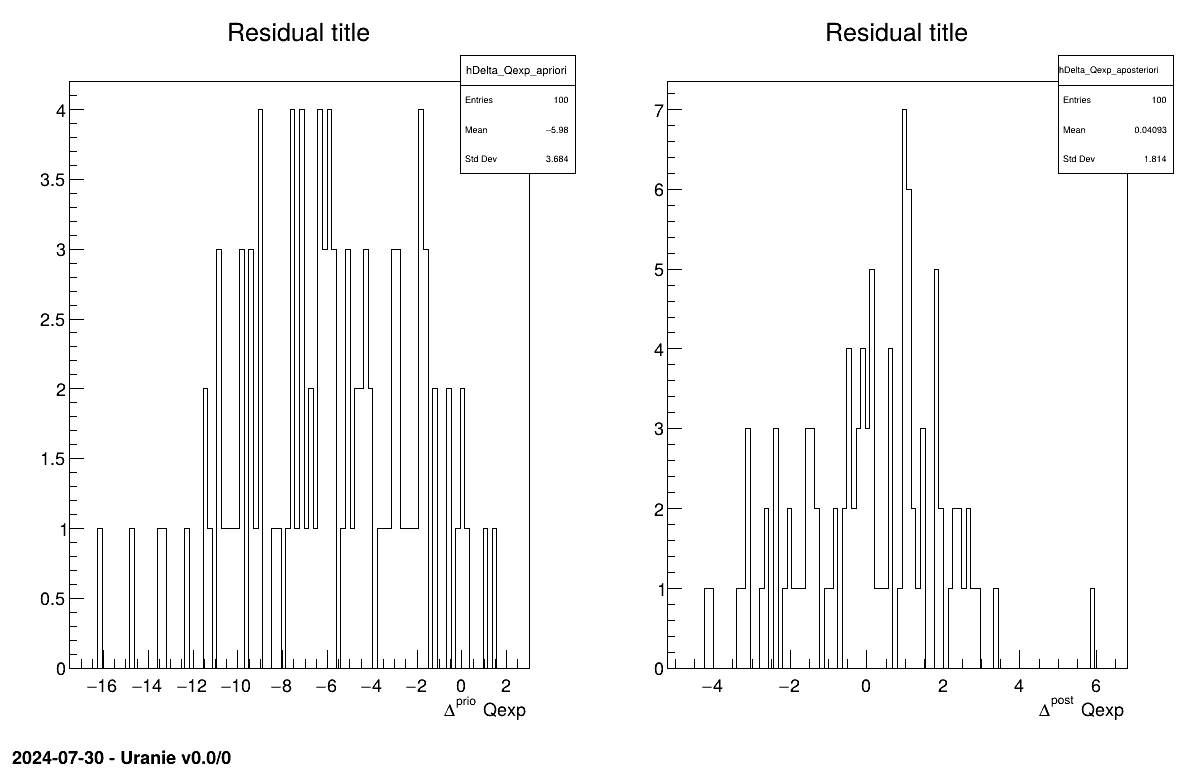
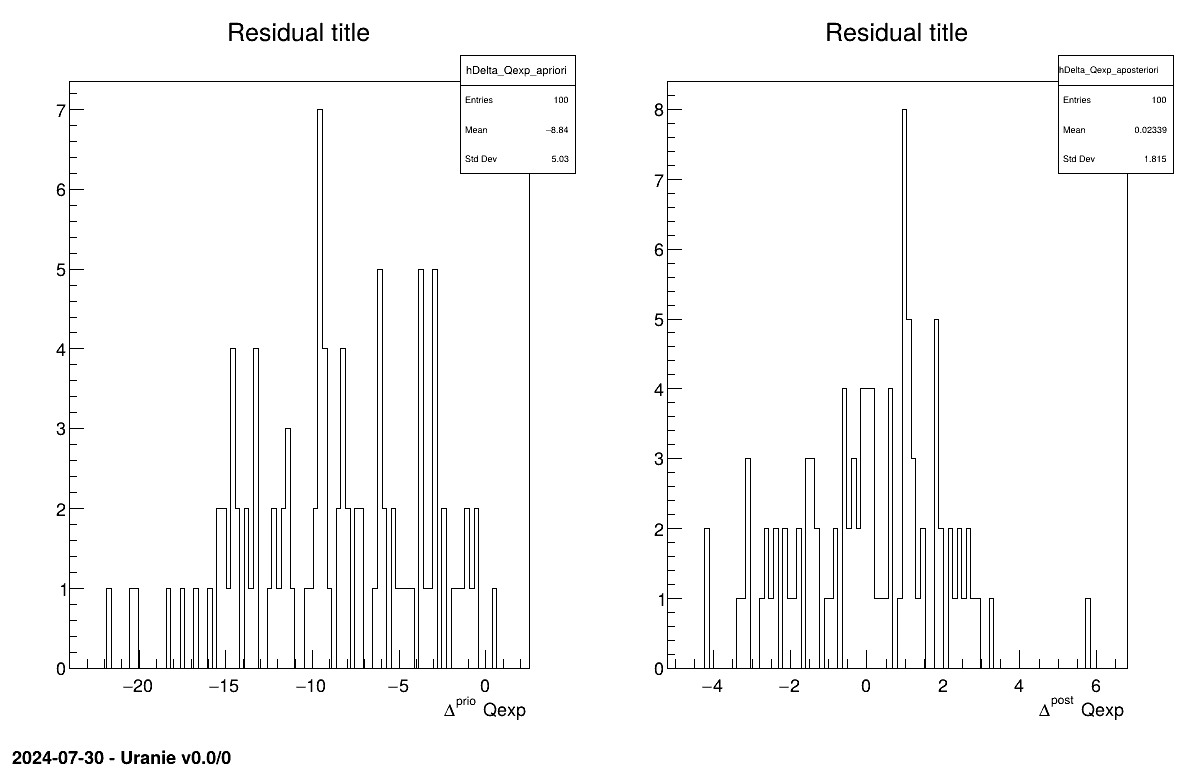
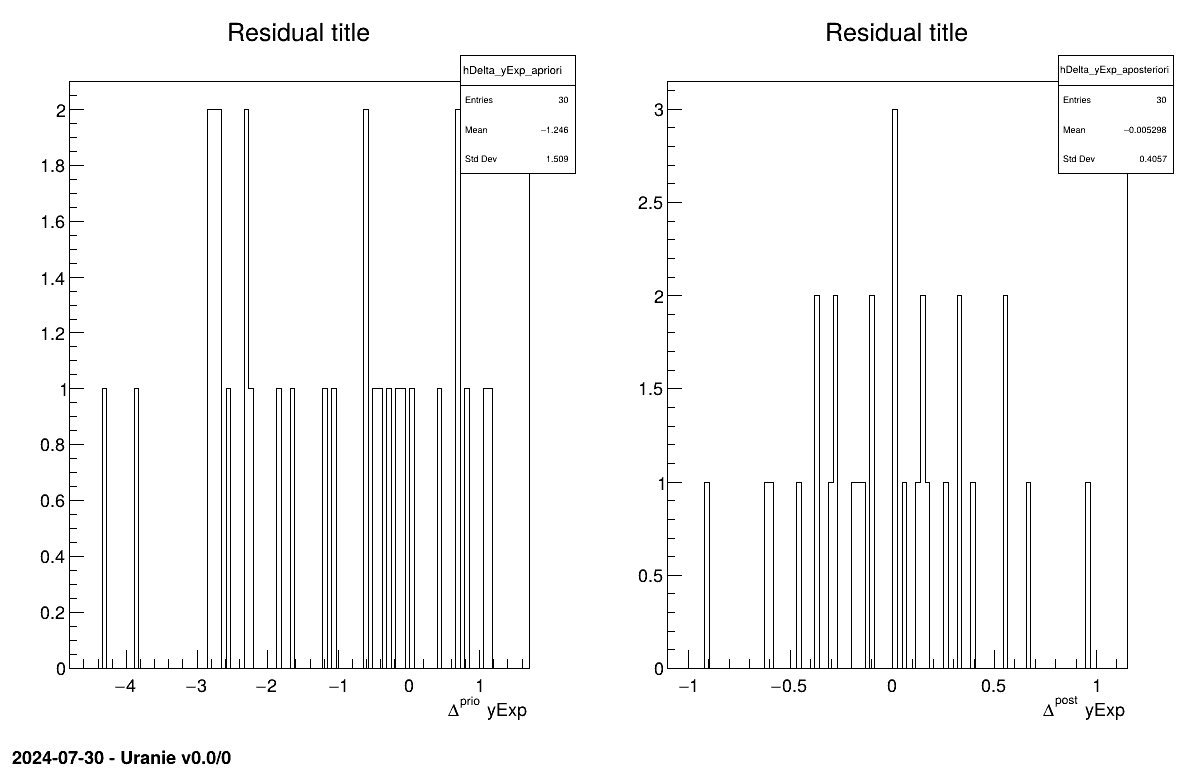
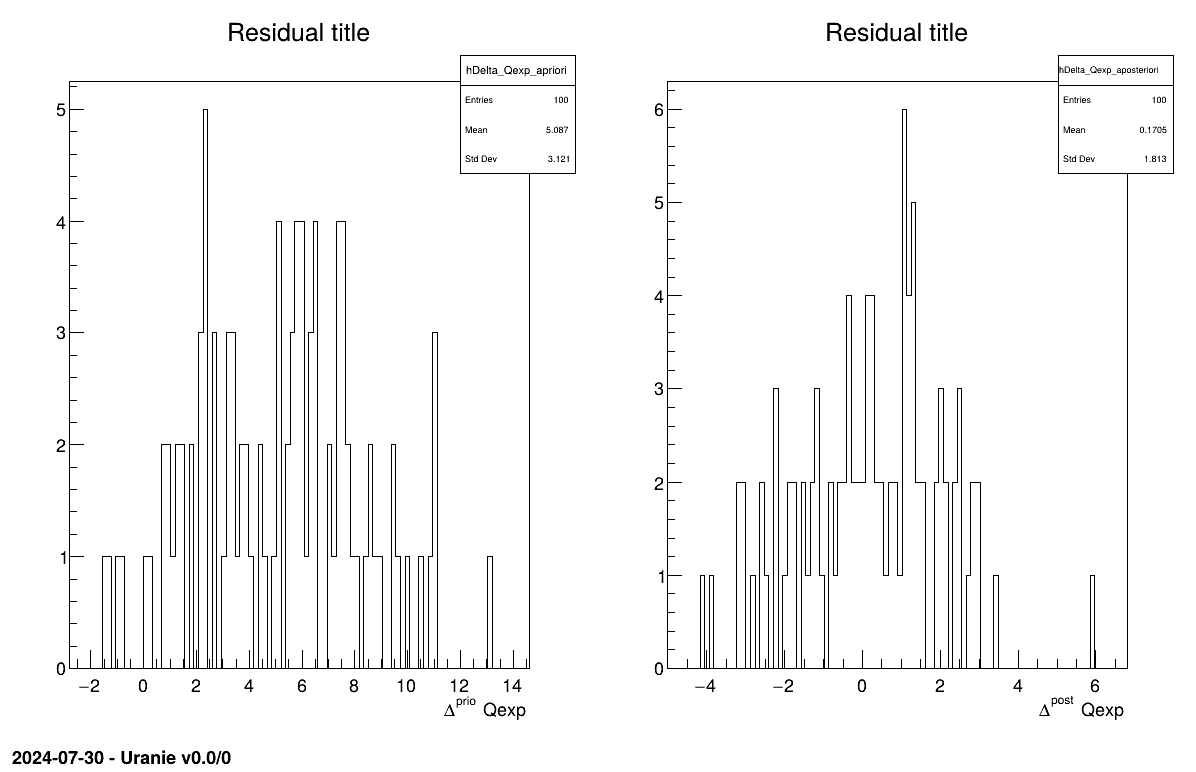
The final part is how to represents part of the results. As this method is a point-estimation there is only one value so it is always displayed on screen, as shown in Section XIV.12.1.3. The other interesting point is to look at the residual, as discussed in [metho] and this is done in Figure XIV.97 which shows normally-distributed residual for the a posteriori estimations.
Processing calibrationMinimisationFlowrate1D.py...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
|....:....|....:....|....:....|....:
.************************************************
* Row * tdsPar__n * hl.hl * agreement *
************************************************
* 0 * 0 * 749.72363 * 18.149368 *
************************************************
The purpose here is to calibrate the value of 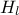 that entered the
that entered the flowrate model, when only two inputs have been varied
(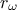 and
and
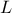 ) while the rest of the
variables are set to a frozen value:
) while the rest of the
variables are set to a frozen value: 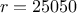 ,
, 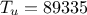 ,
, 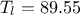 ,
, 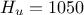 ,
, 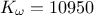 . The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the
. The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the TDataServer
objects). This macro shows how to use linear Bayesian estimation technique, with a Relauncher-architecture.
"""
Example of linear bayesian calibration with simple 1D flowrate model
"""
from rootlogon import ROOT, DataServer, Relauncher, Calibration
# Load the function flowrateCalib1D
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file
ExpData = "Ex2DoE_n100_sd1.75.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
# define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "pouet")
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0))
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
Reg = Relauncher.TCIntEval("flowrateModelnoH")
Reg.addInput(tdsRef.getAttribute("rw"))
Reg.addInput(tdsRef.getAttribute("l"))
Reg.addOutput(DataServer.TAttribute("H"))
runnoH = Relauncher.TSequentialRun(Reg)
runnoH.startSlave()
if runnoH.onMaster():
launch = Relauncher.TLauncher2(tdsRef, runnoH)
launch.solverLoop()
runnoH.stopSlave()
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib1D")
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner = Relauncher.TSequentialRun(Model)
# Set the covariance matrix of the input reference
sd = tdsRef.getValue("sd_eps", 0)
mat = ROOT.TMatrixD(100, 100)
for ival in range(tdsRef.getNPatterns()):
mat[ival][ival] = (sd*sd)
# Set the calibration object
cal = Calibration.TLinearBayesian(tdsPar, runner, 1, "")
cal.setDistanceAndReference("Mahalanobis", tdsRef, "rw:l", "Qexp")
cal.setObservationCovarianceMatrix(mat)
cal.setRegressorName("H")
cal.setParameterTransformationFunction(ROOT.transf)
cal.estimateParameters()
# Draw the parameters
canPar = ROOT.TCanvas("CanPar", "CanPar", 1200, 800)
padPar = ROOT.TPad("padPar", "padPar", 0, 0.03, 1, 1)
padPar.Draw()
padPar.cd()
cal.drawParameters("Parameter title", "*", "", "nonewcanvas,transformed")
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
A very large fraction of this code has been discussed in Section XIV.12.1.2 (from the very start to the sequential run used). The main
difference is the fact that the input parameter is now defined as a TStochasticDistribution
- inheriting object which is the a priori chosen distribution. It can, in this case, only be a
either a TNormalDistribution or a TUniformDistribution (see [metho])
and the latter is the chosen solution here:
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0) )
Another difference with previous example is the fact that we need to prepare a bit the method as we need to get
values for the regressor. As seen in [metho], the linear Bayesian estimation is available when the model can be
considered linear. This means that one should linearise the flowrate function as done here by writing:
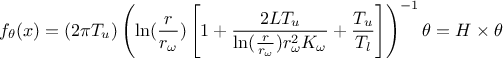
where the
regressor can be expressed as 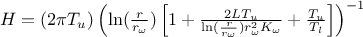 . From there, it is clear that we will be calibrating a newly defined parameter
. From there, it is clear that we will be calibrating a newly defined parameter 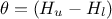 , so we will have to transform that back into our parameter of interest at some point. To get the
regressor estimation we simply use another C++-function
, so we will have to transform that back into our parameter of interest at some point. To get the
regressor estimation we simply use another C++-function flowrateModelnoH along with the
standard Relauncher approach:
# Create interface to assessors
Reg=Relauncher.TCIntEval("flowrateModelnoH")
Reg.addInput(tdsRef.getAttribute("rw"))
Reg.addInput(tdsRef.getAttribute("l"))
Reg.addOutput(DataServer.TAttribute("H") )
runnoH=Relauncher.TSequentialRun(Reg)
runnoH.startSlave()
if runnoH.onMaster():
l=Relauncher.TLauncher2(tdsRef, runnoH)
l.solverLoop()
runnoH.stopSlave()
pass
Moving on, this method also needs the input covariance matrix. The input datasets provided
(Ex2DoE_n100_sd1.75.dat) does contain an estimation of the uncertainty affecting the reference
measurement, this uncertainty being constant throughout the sample, the input covariance is stated to be diagonal
with a constant value set to the standard deviation squared, as, done below:
# Set the covariance matrix of the input reference
sd=tdsRef.getValue("sd_eps",0)
mat=ROOT.TMatrixD(100,100)
for ival in range(tdsRef.getNPatterns()):
mat[ival][ival]=(sd*sd)
pass
The model is anyway defined along with the way to distribute the computation, and then the calibration object is constructed with a Mahalanobis distance function (which is not so relevant as discussed in Section XI.4, as it is only used for illustration purpose). The three important steps are then providing
the input covariance matrix through the
setObservationCovarianceMatrixmethod;the regressors name, by calling
setRegressorName;the parameter transformation function (not compulsory) with the
setParameterTransformationFunction.
The last step is tricky: as we will be performing calibration to get 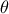 , it would be nice to get the proper parameter value in the
end. This is possible if one provides a C++-function that transform the parameter estimated from the linearisation
back into our parameter of interest. This is done in
, it would be nice to get the proper parameter value in the
end. This is possible if one provides a C++-function that transform the parameter estimated from the linearisation
back into our parameter of interest. This is done in UserFunctions.C for illustration purpose
as it contains this transf function shown below
void transf(double *x, double *res) { res[0] = 1050 - x[0]; } // simply H_l = \theta - H_u The full block of code discussed here is this one
# Set the calibration object
cal=Calibration.TLinearBayesian(tdsPar,runner,1,"")
cal.setDistanceAndReference("Mahalanobis",tdsRef,"rw:l","Qexp")
cal.setObservationCovarianceMatrix(mat)
cal.setRegressorName("H")
cal.setParameterTransformationFunction(ROOT.transf)
cal.estimateParameters()
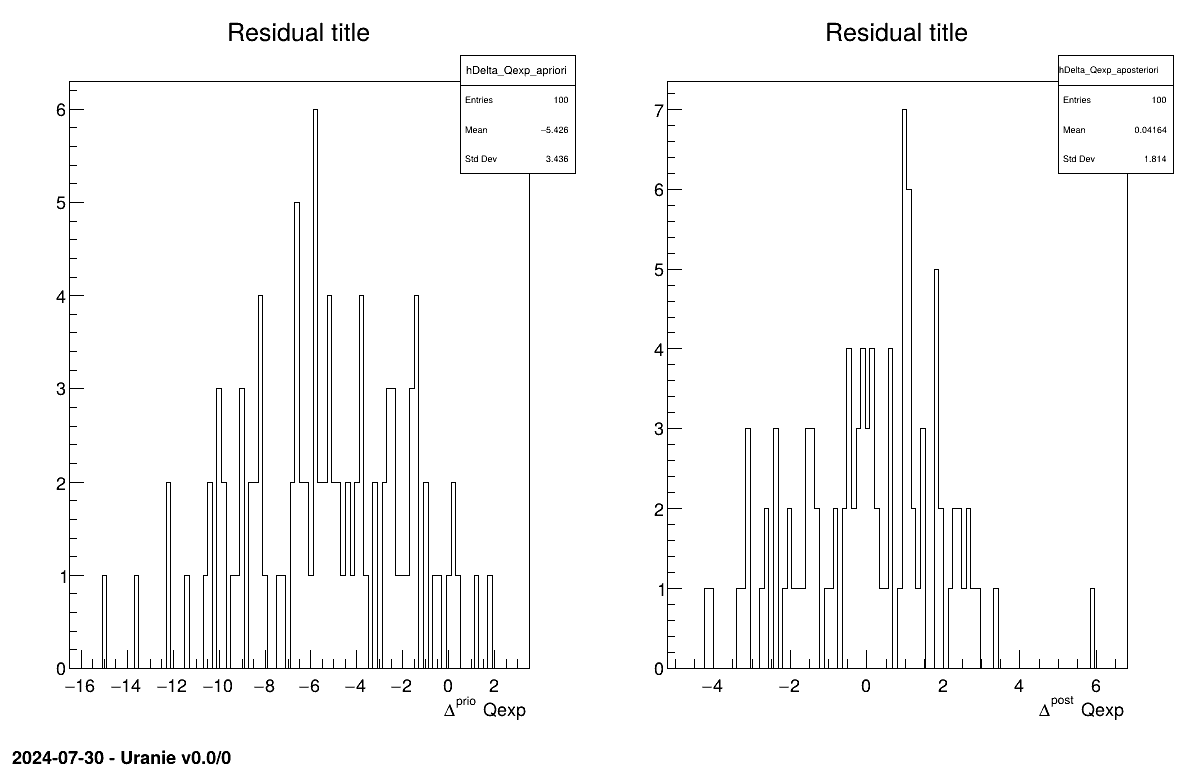
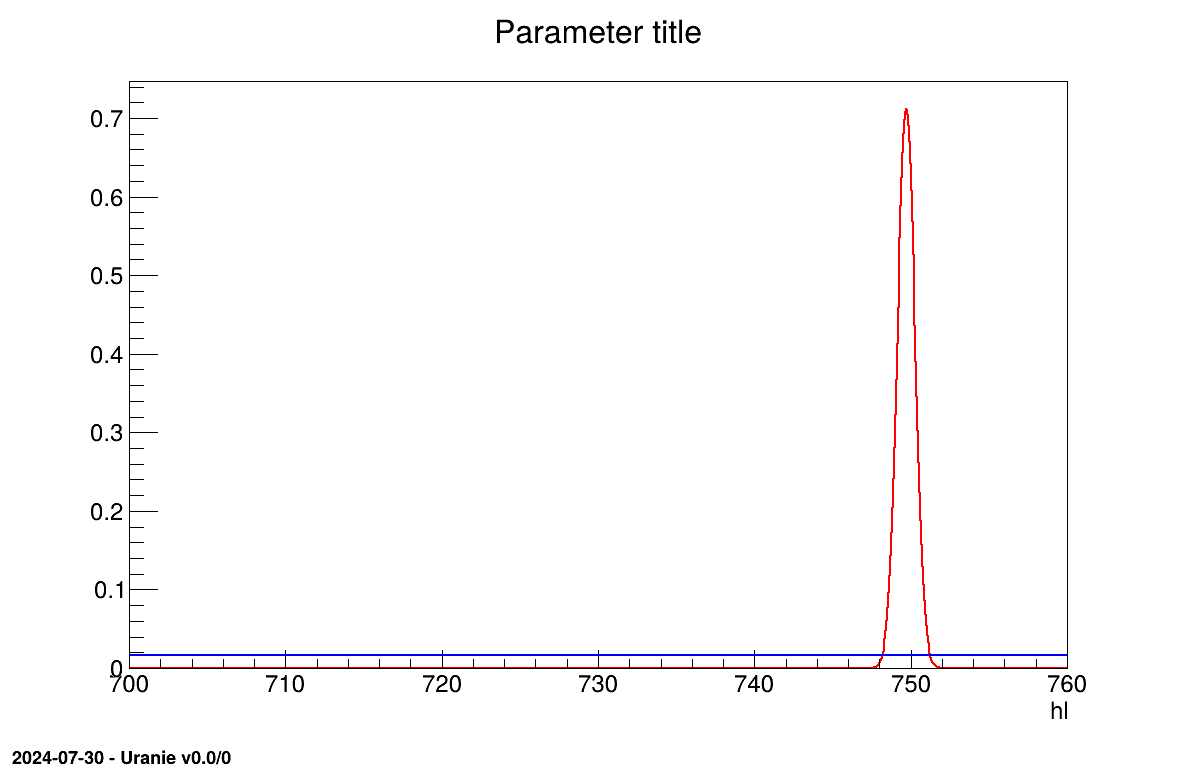
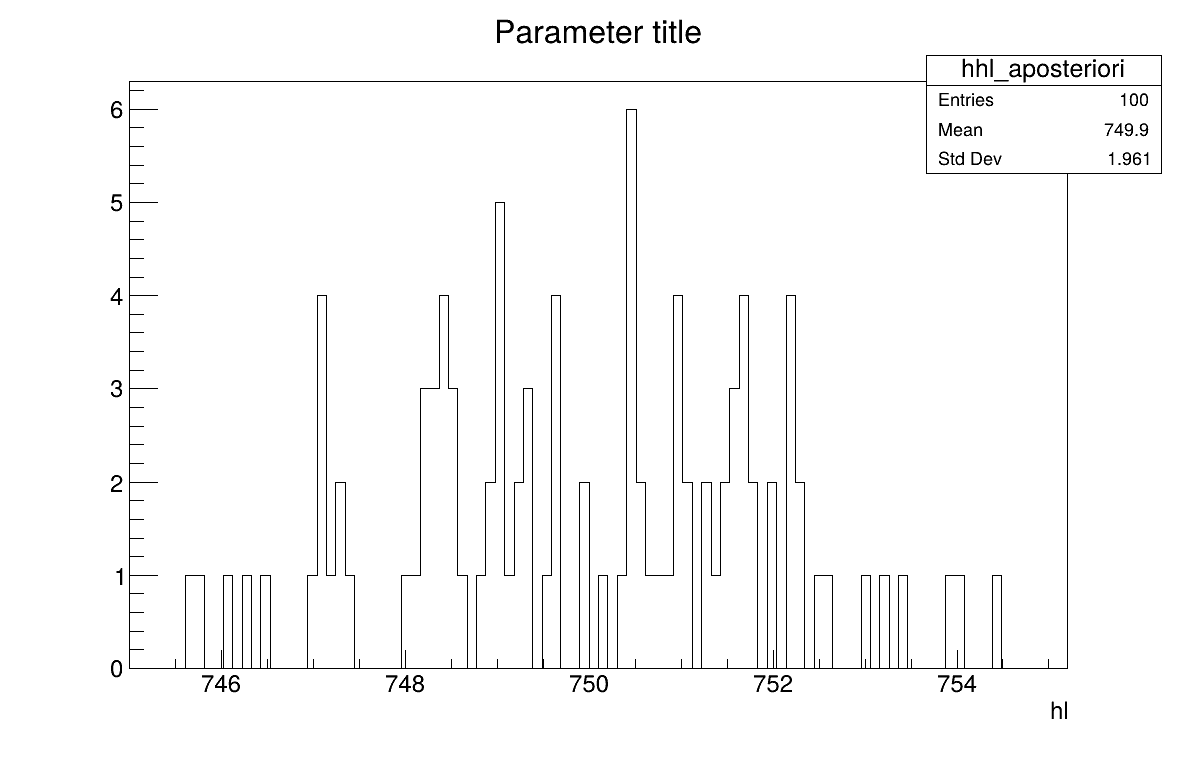
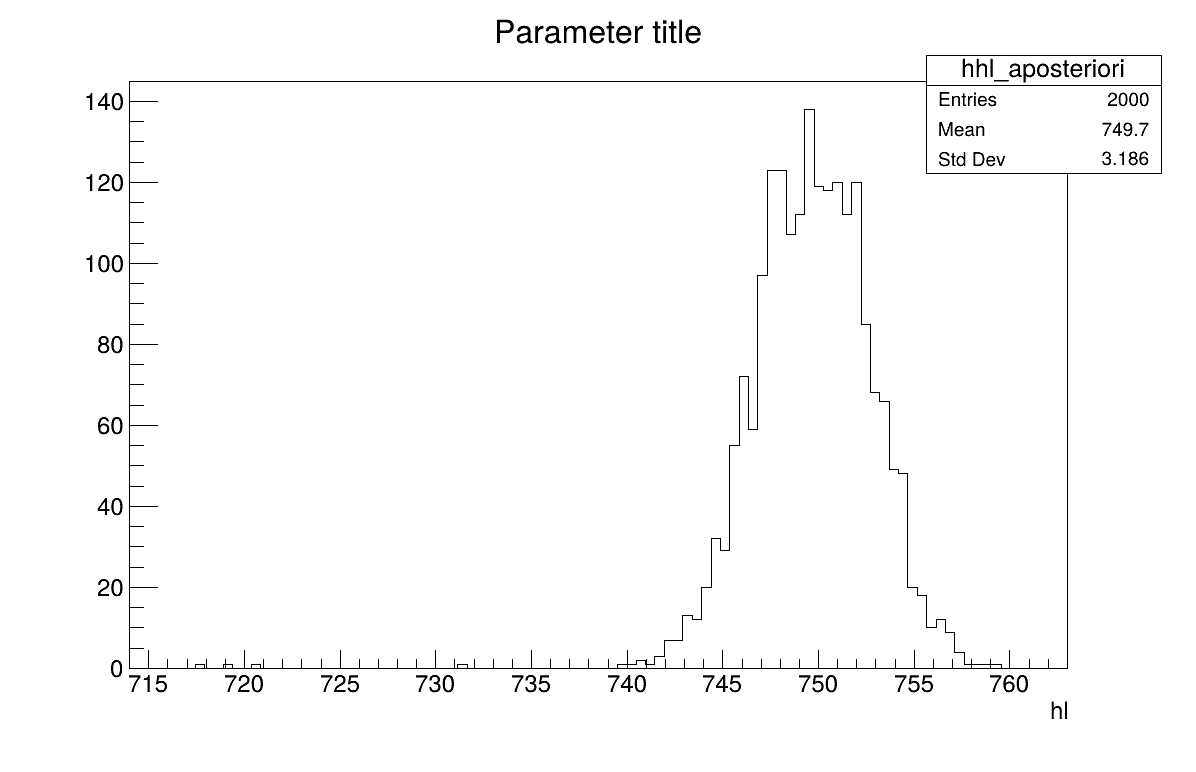
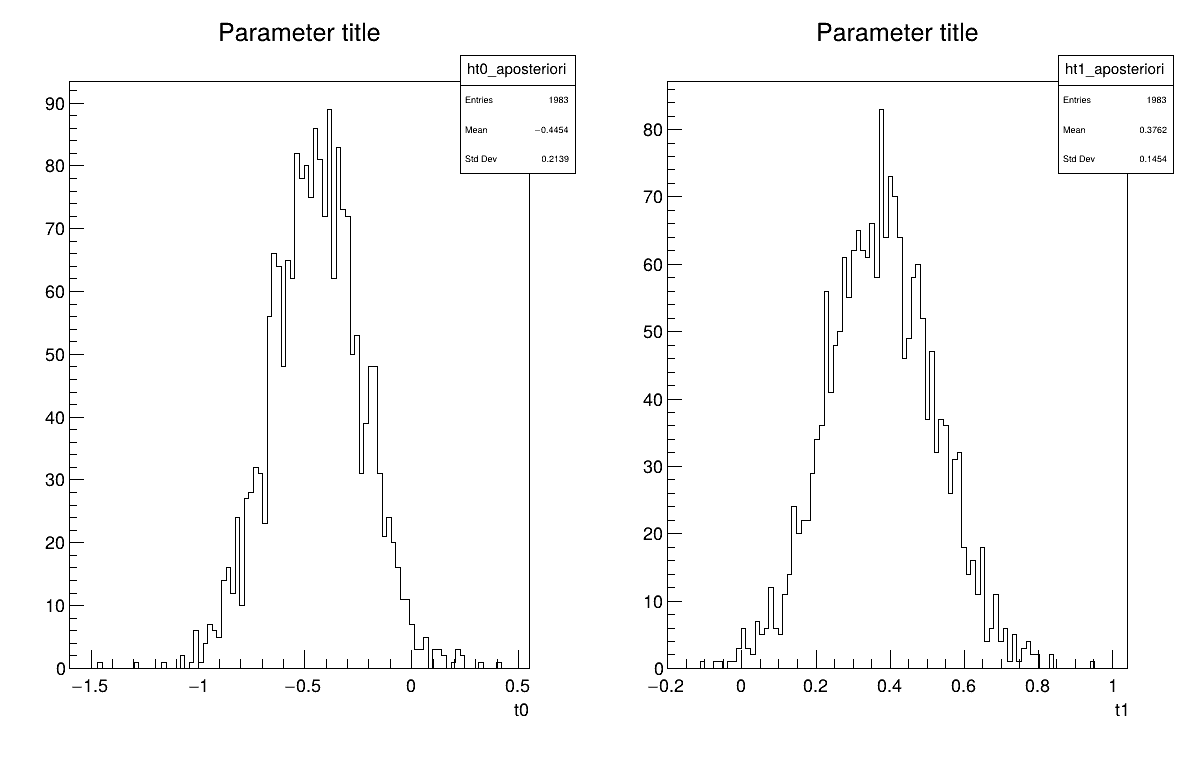
The final part is how to represents part of the results. As this method gives normal a posteriori laws, there defined by a vector of means and a covariance structure which could simply be accessed and the former is shown in on screen, as shown in Section XIV.12.2.3. Two other a posteriori information can be seen as plots: the parameter distribution (shown in Figure XIV.99) and the residual, as discussed in [metho], shown in Figure XIV.98 which shows normally-distributed behaviour.
Processing calibrationLinBayesFlowrate1D.py...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
*** TLinearBayesian::computeParameters(); Transformed parameters estimated are
1x1 matrix is as follows
| 0 |
------------------
0 | 749.7
The purpose here is to calibrate the value of 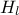 that entered the
that entered the flowrate model, when only two inputs have been varied
(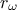 and
and
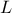 ) while the rest of the
variables are set to a frozen value:
) while the rest of the
variables are set to a frozen value: 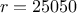 ,
, 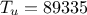 ,
, 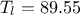 ,
, 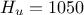 ,
, 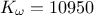 . The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the
. The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the TDataServer
objects). This macro shows how to use the rejection ABC method, with a Relauncher-architecture.
"""
Example of calibration using Rejection ABC approach on flowrate 1D
"""
from rootlogon import ROOT, DataServer, Calibration, Relauncher
# Load the function flowrateCalib1D
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file
ExpData = "Ex2DoE_n100_sd1.75.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
# define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "pouet")
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0))
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib1D")
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner = Relauncher.TSequentialRun(Model)
# Set the calibration object
nABC = 100
eps = 0.05
cal = Calibration.TRejectionABC(tdsPar, runner, nABC, "")
cal.setDistanceAndReference("LS", tdsRef, "rw:l", "Qexp")
cal.setGaussianNoise("sd_eps")
cal.setPercentile(eps)
cal.estimateParameters()
# Draw the parameters
canPar = ROOT.TCanvas("CanPar", "CanPar", 1200, 800)
padPar = ROOT.TPad("padPar", "padPar", 0, 0.03, 1, 1)
padPar.Draw()
padPar.cd()
cal.drawParameters("Parameter title", "*", "", "nonewcanvas")
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
# Compute statistics
tdsPar.computeStatistic()
print("The mean of hl is %3.8g" % (tdsPar.getAttribute("hl").getMean()))
print("The std of hl is %3.8g" % (tdsPar.getAttribute("hl").getStd()))
A very large fraction of this code has been discussed in Section XIV.12.1.2 (from the very start to the sequential run used). The main
difference is the fact that the input parameter is now defined as a TStochasticDistribution
- inheriting object, as a sample will be generated to test locations:
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0) )
Apart from this, the model is defined along with the way to distribute the computation, and then the calibration
object is constructed by defining the number of elements in the final sample (nABC set to 100) and,
here, the percentile of events kept (eps set to 5 percent, which means of total number of estimation
of 2000 locations). As the code is deterministic, the uncertainty model is inserted through a random gaussian noise
whose standard deviation is defined event-by-event thanks to a variable in the observation dataserver. The distance
is also define and the estimation is performed.
# Set the calibration object
nABC = 100; eps = 0.05
cal = Calibration.TRejectionABC(tdsPar, runner, nABC, "")
cal.setDistanceAndReference("LS",tdsRef,"rw:l","Qexp")
cal->setGaussianNoise("sd_eps");
cal.setPercentile(eps)
cal.estimateParameters()
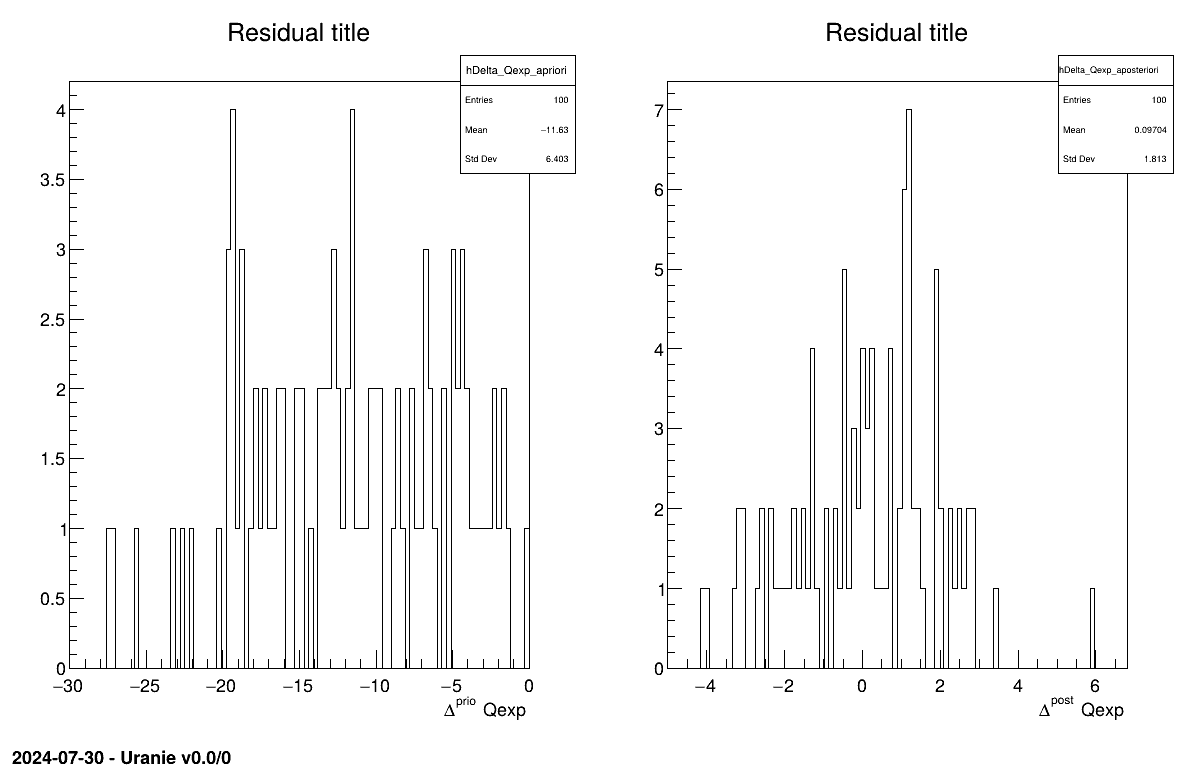
The final part is how to represents part of the results. As this method gives a sample, the first two lines give basic statistical information, directly on screen, as shown in Section XIV.12.3.3. Two other a posteriori information can be seen as plots: the parameter distribution (shown in Figure XIV.101) and the residual, as discussed in [metho], shown in Figure XIV.100 which shows normally-distributed behaviour.
Processing calibrationRejectionABCFlowrate1D.py...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
<URANIE::INFO>
<URANIE::INFO> *** URANIE INFORMATION ***
<URANIE::INFO> *** File[${SOURCEDIR}/meTIER/calibration/souRCE/TDistanceFunction.cxx] Line[601]
<URANIE::INFO> TDistanceFunction::setGaussianRandomNoise: gaussian random noise(s) is added using information in [sd_eps] to modify the output variable(s) [out].
<URANIE::INFO> *** END of URANIE INFORMATION ***
<URANIE::INFO>
<URANIE::INFO>
<URANIE::INFO> *** URANIE INFORMATION ***
<URANIE::INFO> *** File[${SOURCEDIR}/meTIER/calibration/souRCE/TRejectionABC.cxx] Line[107]
<URANIE::INFO> TRejectionABC::computeParameters:: 2000 evaluations will be performed !
<URANIE::INFO> *** END of URANIE INFORMATION ***
<URANIE::INFO>
A posteriori mean coordinates are : (749.926)
The mean of hl is 749.92609
The std of hl is 1.9704229
The purpose here is to calibrate the value of 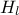 that entered the
that entered the flowrate model, when only two inputs have been varied
(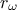 and
and
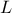 ) while the rest of the
variables are set to a frozen value:
) while the rest of the
variables are set to a frozen value: 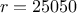 ,
, 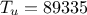 ,
, 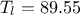 ,
, 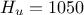 ,
, 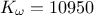 . The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the
. The context has been already discussed in Section XI.2.4
(including discussing the model, here using the model as a C++-function and the first few lines defining the TDataServer
objects). This macro shows how to use Markov-chain approach with the metropolis-hasting algorithm, using a
Relauncher-architecture.
"""
Example of Metropolis Hasting usage on simple flowrate 1D model
"""
from rootlogon import ROOT, DataServer, Relauncher, Calibration
# Load the function flowrateCalib1D
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file$
ExpData = "Ex2DoE_n100_sd1.75.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
tdsRef.addAttribute("wei_exp", "1./(sd_eps*sd_eps)")
# define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "pouet")
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0))
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib1D")
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner = Relauncher.TSequentialRun(Model)
# Set the calibration object
cal = Calibration.TMetropHasting(tdsPar, runner, 2000, "")
cal.setDistanceAndReference("weightedLS", tdsRef, "rw:l", "Qexp", "wei_exp")
cal.setNbDump(400)
cal.setAcceptationRatioRange(0.4, 0.45)
cal.estimateParameters()
# Quality assessment : Draw the trace the MCMC
canTr = ROOT.TCanvas("CanTr", "CanTr", 1200, 800)
padTr = ROOT.TPad("padTr", "padTr", 0, 0.03, 1, 1)
padTr.Draw()
padTr.cd()
cal.drawTrace("Trace title", "*", "", "nonewcanvas")
# Draw the parameters
canPar = ROOT.TCanvas("CanPar", "CanPar", 1200, 800)
padPar = ROOT.TPad("padPar", "padPar", 0, 0.03, 1, 1)
padPar.Draw()
padPar.cd()
cal.drawParameters("Parameter title", "*", "", "nonewcanvas")
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
# Compute the auto-correlation
burn = 20 # Remove first 20 elements
lag = ROOT.std.vector('int')([1, 5, 10, 20])
autoCorr = ROOT.std.vector['double'](range(lag.size()))
cal.getAutoCorrelation(lag, autoCorr, burn)
print("Autocorrelation are " + str(autoCorr.size()) + ":")
for il in range(lag.size()):
output = "*** for lag=" + str(lag[il]) + ": "
for ip in range(cal.getNPar()):
output += "%1.6g" % (autoCorr[ip*lag.size()+il])
print(output)
A very large fraction of this code has been discussed in Section XIV.12.1.2 (from the very start to the sequential run used). The main
difference is the fact that the input parameter is now defined as a TStochasticDistribution
- inheriting object, as a sample will be generated to test locations:
tdsPar.addAttribute(DataServer.TUniformDistribution("hl", 700.0, 760.0) )
Apart from this, the model is defined along with the way to distribute the computation, and then the calibration object is constructed by defining the number of elements in the final sample (set to 2000). The distance function is then defined and two properties are set along: the threshold to which a new line is dump on screen to provide information and the acceptation ratio to be kept by playing on the standard deviation of the research (see Section XI.6). Finally the estimation is performed.
# Set the calibration object
cal = Calibration.TMetropHasting(tdsPar,runner,2000,"")
cal.setDistanceAndReference("weightedLS",tdsRef,"rw:l","Qexp","wei_exp")
cal.setNbDump(400)
cal.setAcceptationRatioRange(0.4, 0.45)
cal.estimateParameters()
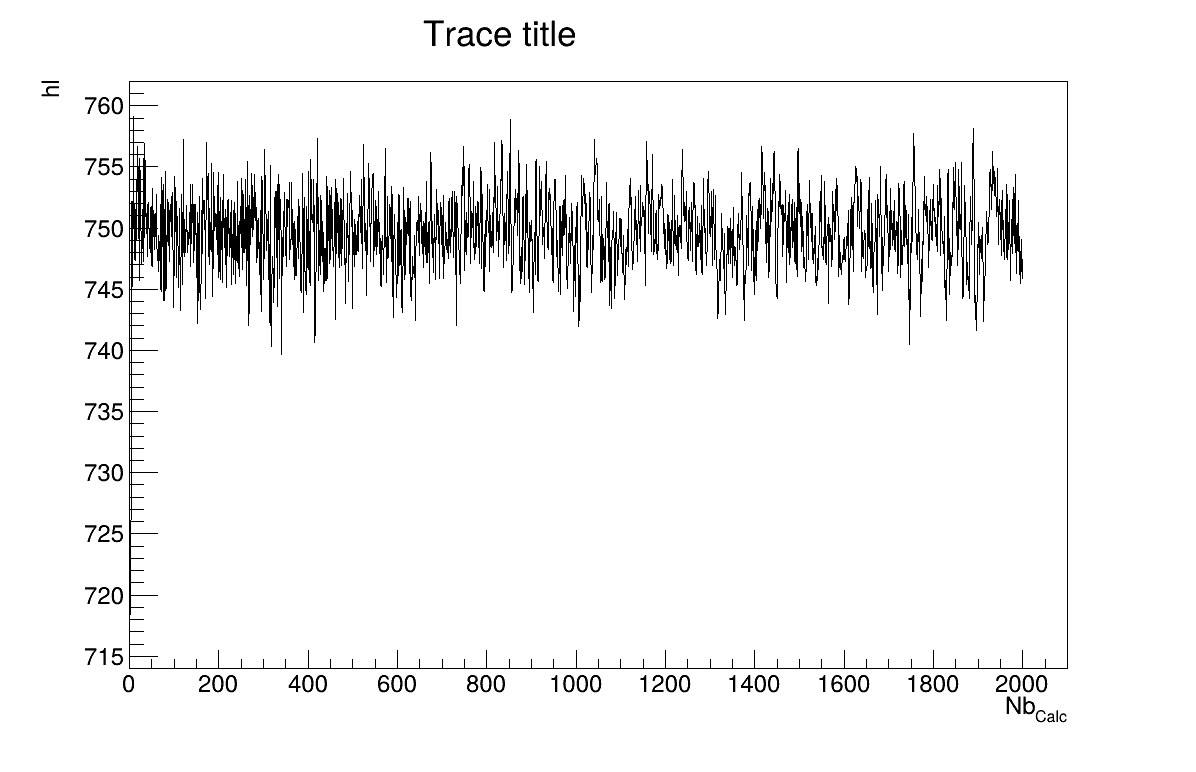
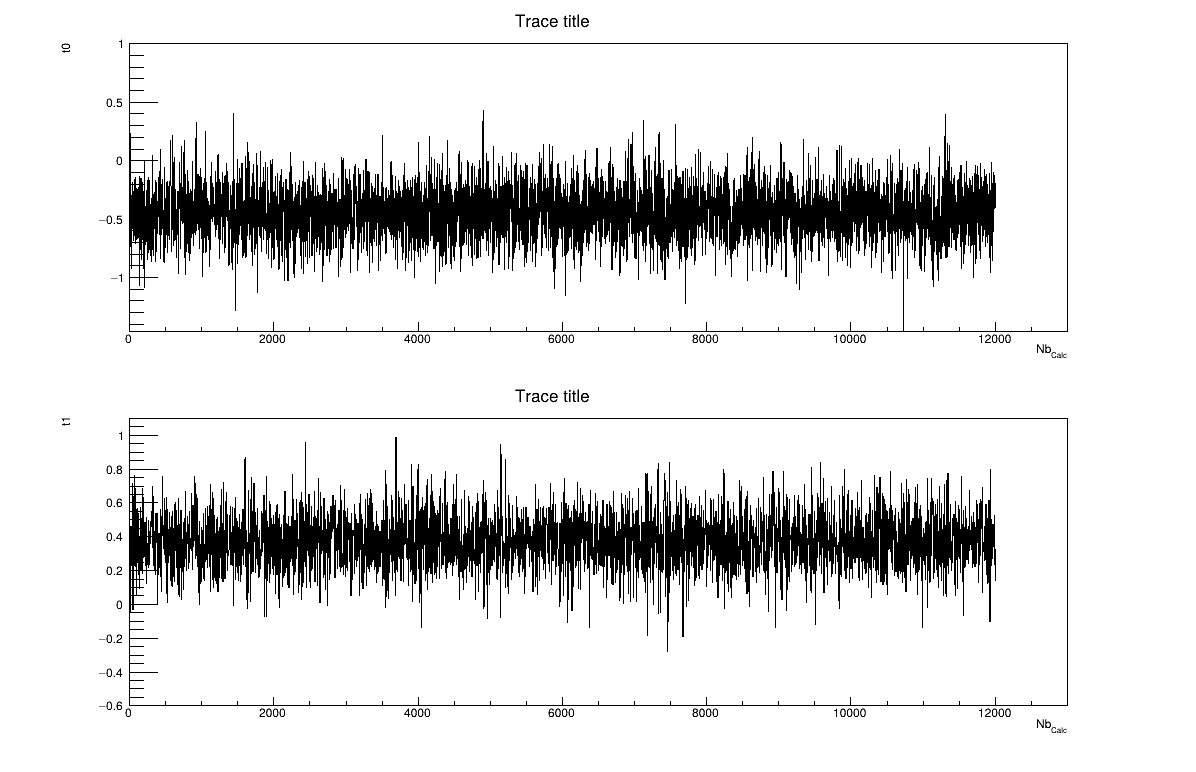
The final part is how to represents part of the results. At first one should look at the trace to check for any peculiar trend and choose a burn-in threshold if needed (see Section XI.6), which is shown in Figure XIV.102. As this method gives a sample, the first two lines give basic statistical information, directly on screen, as shown in Section XIV.12.4.3. Two other a posteriori information can be seen as plots: the parameter distribution (shown in Figure XIV.104) and the residual, as discussed in [metho], shown in Figure XIV.103 which shows normally-distributed behaviour.
Finally, the auto-correlation of the resulting sample can be computed with different lag values (see Section XI.6), as by definition, elements from a Markov-chain are not fully independent. This is done
here by calling the getAutoCorrelation method which provides as many estimations as one
request, for the lag values. The results are show on screen (see Section XIV.12.4.3) and are used for post-processing analysis, as the trace
plot discussed above. It is interesting to notice here that the vector can be handled thanks to the
latest version of ROOT which allow this method to give the results through a reference-passing prototype.
# Compute the auto-correlation
burn=20
lag=ROOT.std.vector('int')([1,5,10,20])
autoCorr=ROOT.std.vector['double'](range(lag.size()))
cal.getAutoCorrelation(lag, autoCorr, burn)
print("Autocorrelation are "+str(autoCorr.size())+":")
for il in range(lag.size()):
output="*** for lag="+str(lag[il])+": "
for ip in range(cal.getNPar()):
output+="%1.6g"%(autoCorr[ip*lag.size()+il])
pass
print(output)
pass
Processing calibrationMetropHastingFlowrate1D.py...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
400 events done
800 events done
1200 events done
1600 events done
A posteriori mean coordinates are : (749.66)
Autocorrelation are 4:
*** for lag=1: 0.409977
*** for lag=5: 0.0365494
*** for lag=10: 0.0138947
*** for lag=20: 0.0773913
The purpose here is to calibrate the value of 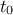 and
and 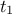 in a
very simple linear model where both parameters are respectively the constant term and the multiplicative
coefficient of the only input variable. The input file is
in a
very simple linear model where both parameters are respectively the constant term and the multiplicative
coefficient of the only input variable. The input file is linReg_Database.dat and the toy
model is stored in UserFunctions.C. This macro illustrates the steps in two dimensions to get
a sample, estimate the burn-in and lag (if needed) and plot the resulting distribution.
"""
Example of calibration using MH algo on linear model
"""
from rootlogon import ROOT, DataServer, Relauncher, Calibration
# Load the function flowrateCalib1D
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file
ExpData = "linReg_Database.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
# Define the uncertainty model wih a guess
sd_exp = 0.2
tdsRef.addAttribute("wei_exp", "1./("+str(sd_exp)+"*"+str(sd_exp)+")")
# Define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "poute")
binf_sea = -2.0
bsup_sea = 2.0
tdsPar.addAttribute(DataServer.TUniformDistribution("t0", binf_sea, bsup_sea))
tdsPar.addAttribute(DataServer.TUniformDistribution("t1", binf_sea, bsup_sea))
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
myeval = Relauncher.TCIntEval("Toy")
myeval.addInput(tdsRef.getAttribute("x"))
myeval.addInput(tdsPar.getAttribute("t0"))
myeval.addInput(tdsPar.getAttribute("t1"))
myeval.addOutput(out)
# Set the runner
run = Relauncher.TSequentialRun(myeval)
# Set the calibration object
# Providing wild guess for value and variation range
inval = ROOT.std.vector['double']([0.8, -0.6])
std = ROOT.std.vector['double']([0.4, 0.5])
ns = 12000
cal = Calibration.TMetropHasting(tdsPar, run, ns, "")
cal.setDistanceAndReference("weightedLS", tdsRef, "x", "yExp", "wei_exp")
cal.setNbDump(4000)
cal.setInitialisation(inval, std)
cal.estimateParameters()
# Quality assessment : Draw the trace the MCMC
canTr = ROOT.TCanvas("CanTr", "CanTr", 1200, 800)
padTr = ROOT.TPad("padTr", "padTr", 0, 0.03, 1, 1)
padTr.Draw()
padTr.cd()
cal.drawTrace("Trace title", "*", "", "nonewcanvas")
# Quality assessment : Draw the trace the MCMC
canAcc = ROOT.TCanvas("CanAcc", "CanAcc", 1200, 800)
padAcc = ROOT.TPad("padAcc", "padAcc", 0, 0.03, 1, 1)
padAcc.Draw()
padAcc.cd()
cal.drawAcceptationRatio("AcceptRatio title", "*", "", "nonewcanvas")
burn = 100 # Remove first 100 elements
# Compute the auto-correlation
lag = ROOT.std.vector('int')([1, 3, 6, 10, 20])
autoCorr = ROOT.std.vector['double'](range(lag.size()))
cal.getAutoCorrelation(lag, autoCorr, burn)
print("Autocorrelation are:")
for il in range(lag.size()):
output = "*** for lag="+str(lag[il])+": "
for ip in range(cal.getNPar()):
output += "%1.6g" % (autoCorr[ip*lag.size()+il])
print(output)
mylag = 6
# Define a selection based on burn-in and lag
mycut = "(%s > %d) && ((%s %% %d) == 0)" % (tdsPar.getIteratorName(), burn,
tdsPar.getIteratorName(), mylag)
# Draw the parameters
canPar = ROOT.TCanvas("CanPar", "CanPar", 1200, 800)
padPar = ROOT.TPad("padPar", "padPar", 0, 0.03, 1, 1)
padPar.Draw()
padPar.cd()
cal.drawParameters("Parameter title", "*", mycut, "nonewcanvas")
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
This macro starts, as usual by defining both reference and parameter dataservers. The only specific lines here are these lines used later-on in which we define the uncertainty hypothesis, meaning a guess of the uncertainty by creating the weight variable (constant throughout the 30 reference bservations)
# Define the uncertainty model wih a guess
sd_exp=0.2
tdsRef.addAttribute("wei_exp","1./("+str(sd_exp)+"*"+str(sd_exp)+")")
This macro continues by defining the model and the way to run it. The instance created here, is a
TCIntEval which simply request the three input variables discussed above in the correct order. Here the first one has to be the input variable, whose values are coming
from the reference datasets, while the other ones are the parameters to be calibrated, because of the way the
C++-function has been defined. Once done, the output attribute is added (as our model computes only one variable)
and the chosen distribution strategy is chosen to be sequential.
# Create interface to assessors
myeval=Relauncher.TCIntEval("Toy")
myeval.addInput(tdsRef.getAttribute("x"))
myeval.addInput(tdsPar.getAttribute("t0"))
myeval.addInput(tdsPar.getAttribute("t1"))
myeval.addOutput(out)
# Set the runner
run=Relauncher.TSequentialRun(myeval)
Apart from this, the model is defined along with the way to distribute the computation, and then the calibration object is constructed by defining the number of elements in the final sample (set to 12000). The distance function is then defined and two properties are set along: the threshold to which a new line is dump on screen to provide information and the initialisation properties (values and variation ranges, see Section XI.6). Finally the estimation is performed.
# Set the calibration object
# Providing wild guess for value and variation range
inval=ROOT.std.vector['double']([0.8, -0.6]); std=ROOT.std.vector['double']([0.4, 0.5])
ns=12000
cal=Calibration.TMetropHasting(tdsPar, run, ns,"")
cal.setDistanceAndReference("weightedLS",tdsRef,"x","yExp","wei_exp")
cal.setNbDump(4000)
cal.setInitialisation(inval, std)
cal.estimateParameters(
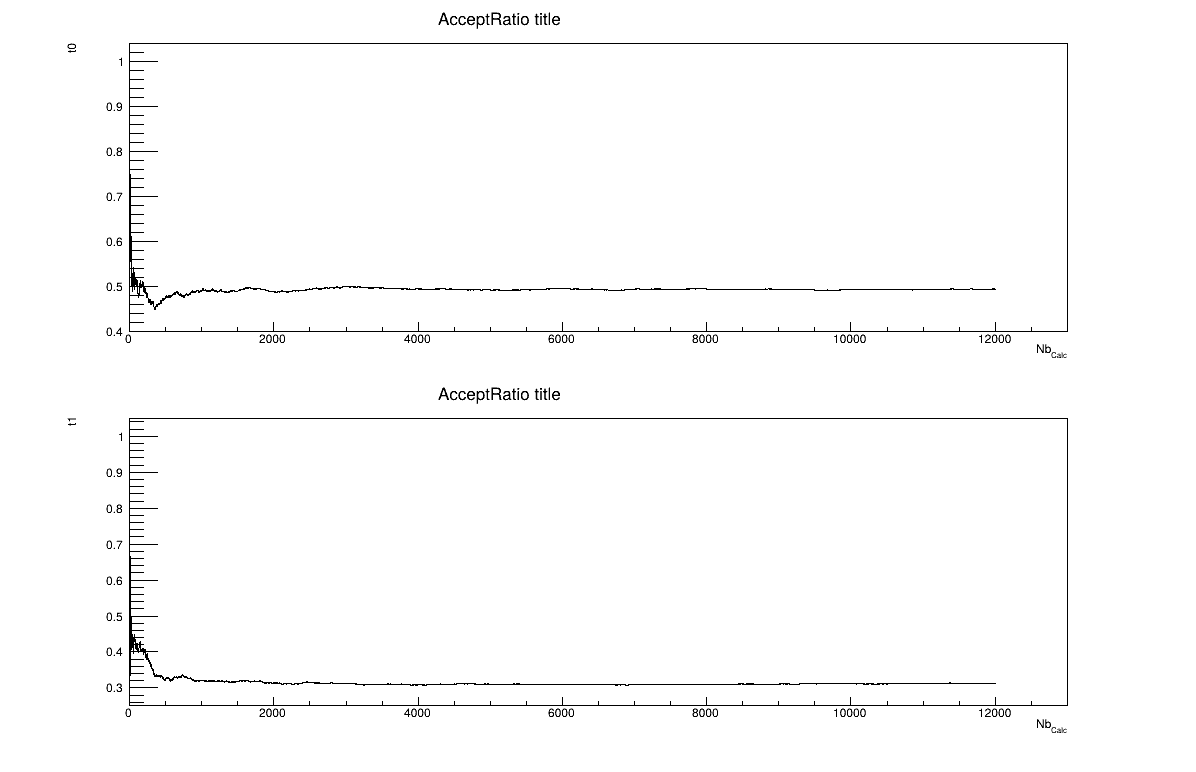
The final part is how to represents part of the results. At first one should look at the trace to check for any peculiar trend and choose a burn-in threshold if needed (see Section XI.6), which is shown in Figure XIV.105, but one can also look at the acceptation ratio plots show in Figure XIV.106. As this method gives a sample, the first two lines give basic statistical information, directly on screen, as shown in Section XIV.12.5.3. One can also look at the autocorrelation and this might lead to the choice of a lag value to get low autocorrelation values (as shown in the console below).
Given both burn-in and lag values set, two other a posteriori information can be seen as plots: the parameter distribution (shown in Figure XIV.108) and the residual, as discussed in [metho], shown in Figure XIV.107 which shows normally-distributed behaviour.
Processing calibrationMetropHastingLinReg.C...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
4000 events done
8000 events done
12000 events done
A posteriori mean coordinates are : (-0.441188,0.373825)
Autocorrelation are:
*** for lag=1: 0.598494; 0.629943;
*** for lag=3: 0.189151; 0.205056;
*** for lag=6: 0.0542879; 0.0667108;
*** for lag=10: 0.0160068; 0.0195018;
*** for lag=20: 0.0363133; 0.00163761;
The purpose here is to calibrate the value both of 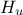 and
and 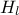 that entered the
that entered the flowrate model, when only two inputs have been varied
(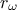 and
and
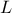 ) while the rest of the
variables are set to a frozen value:
) while the rest of the
variables are set to a frozen value: 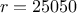 ,
, 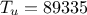 ,
, 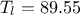 ,
, 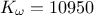 . The context is the same as the one discussed in Section XIV.12.1 but it describes two things:
. The context is the same as the one discussed in Section XIV.12.1 but it describes two things:
using Vizir instead of a more simple
TNloptSolver-inheriting instancediscuss the identifiability of a problem, introduced in [metho]
The model is the function flowrateCalib2D which is the same as the
flowrateClib1D just requesting the 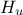 variable as first input.
variable as first input.
"""
Example of calibration through minimisation with Vizir in Flowrate 2D
"""
from rootlogon import ROOT, DataServer, Relauncher, Reoptimizer, Calibration
# Load the function flowrateCalib2DVizir
ROOT.gROOT.LoadMacro("UserFunctions.C")
# Input reference file
ExpData = "Ex2DoE_n100_sd1.75.dat"
# define the reference
tdsRef = DataServer.TDataServer("tdsRef", "doe_exp_Re_Pr")
tdsRef.fileDataRead(ExpData)
# define the parameters
tdsPar = DataServer.TDataServer("tdsPar", "pouet")
tdsPar.addAttribute(DataServer.TAttribute("hu", 1020.0, 1080.0))
tdsPar.addAttribute(DataServer.TAttribute("hl", 720.0, 780.0))
# Create the output attribute
out = DataServer.TAttribute("out")
# Create interface to assessors
Model = Relauncher.TCIntEval("flowrateCalib2D")
Model.addInput(tdsPar.getAttribute("hu"))
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner = Relauncher.TSequentialRun(Model)
# Set the calibration object
cal = Calibration.TMinimisation(tdsPar, runner, 1)
cal.setDistanceAndReference("relativeLS", tdsRef, "rw:l", "Qexp")
# Set optimisaiton properties
solv = Reoptimizer.TVizirGenetic()
solv.setSize(24, 15000, 100)
cal.setOptimProperties(solv)
# cal.getOptimMaster().setTolerance(1e-6)
cal.estimateParameters()
# Draw the Residual
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("tutu", "*", "", "nonewcanvas")
# Draw the box plot of parameters
canPar = ROOT.TCanvas("CanPar", "CanPar", 1200, 800)
tdsPar.getTuple().SetMarkerStyle(20)
tdsPar.getTuple().SetMarkerSize(0.8)
tdsPar.Draw("hu:hl")
# Look at the correlation and statistic
tdsPar.computeStatistic("hu:hl")
corr = tdsPar.computeCorrelationMatrix("hu:hl")
corr.Print()
print("hl is %3.8g +- %3.8g " % (tdsPar.getAttribute("hl").getMean(),
tdsPar.getAttribute("hl").getStd()))
print("hu is %3.8g +- %3.8g " % (tdsPar.getAttribute("hu").getMean(),
tdsPar.getAttribute("hu").getStd()))
# Draw the residuals
canRes = ROOT.TCanvas("CanRes", "CanRes", 1200, 800)
padRes = ROOT.TPad("padRes", "padRes", 0, 0.03, 1, 1)
padRes.Draw()
padRes.cd()
cal.drawResidues("Residual title", "*", "", "nonewcanvas")
Apart from the first lines discussed in Section XI.2.4, the important line is the
one defining the variable, here as TAttribute with boundaries to define the phase space in
which the algorithm will look for:
tdsPar.addAttribute(DataServer.TAttribute("hu", 1020.0, 1080.0) )
tdsPar.addAttribute(DataServer.TAttribute("hl", 720.0, 780.0) )
This macro continues by defining the model and the way to run it. The instance created here, is a
TCIntEval which simply request the three input variables discussed above in the correct order. Here the first ones have to be 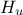 and
and 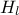 , the parameter that we want to calibrate, because of the way the C++-function has been defined
and then the two varying ones, (
, the parameter that we want to calibrate, because of the way the C++-function has been defined
and then the two varying ones, (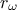 and
and 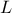 ) whose
values are coming from the reference input file. Once done, the output attribute is added (as our model computes
only one variable) and the chosen distribution strategy is chosen to be sequential.
) whose
values are coming from the reference input file. Once done, the output attribute is added (as our model computes
only one variable) and the chosen distribution strategy is chosen to be sequential.
# Create interface to assessors
Model=Relauncher.TCIntEval("flowrateCalib2D")
Model.addInput(tdsPar.getAttribute("hu"))
Model.addInput(tdsPar.getAttribute("hl"))
Model.addInput(tdsRef.getAttribute("rw"))
Model.addInput(tdsRef.getAttribute("l"))
Model.addOutput(out)
# Set the runner
runner=Relauncher.TSequentialRun(Model)
Once done the calibration object (TMinimisation) is created and, as discussed in Section XI.2.2.1, the first object to be created is the distance function (here the
least-square one) through the setDistanceAndReference, that also defines the TDataServer that
contains reference data, the name of the reference inputs and the reference variable to which the output of the
model should be compared with. Finally the optimisation algorithm is defined by creating an instance of
TVizirGenetic and then the parameters are estimated.
# Set the calibration object
cal=Calibration.TMinimisation(tdsPar,runner,1)
cal.setDistanceAndReference("relativeLS",tdsRef,"rw:l","Qexp")
# Set optimisaiton properties
solv=Reoptimizer.TVizirGenetic()
solv.setSize(24,15000,100)
cal.setOptimProperties(solv)
#cal.getOptimMaster().setTolerance(1e-6)
cal.estimateParameters()
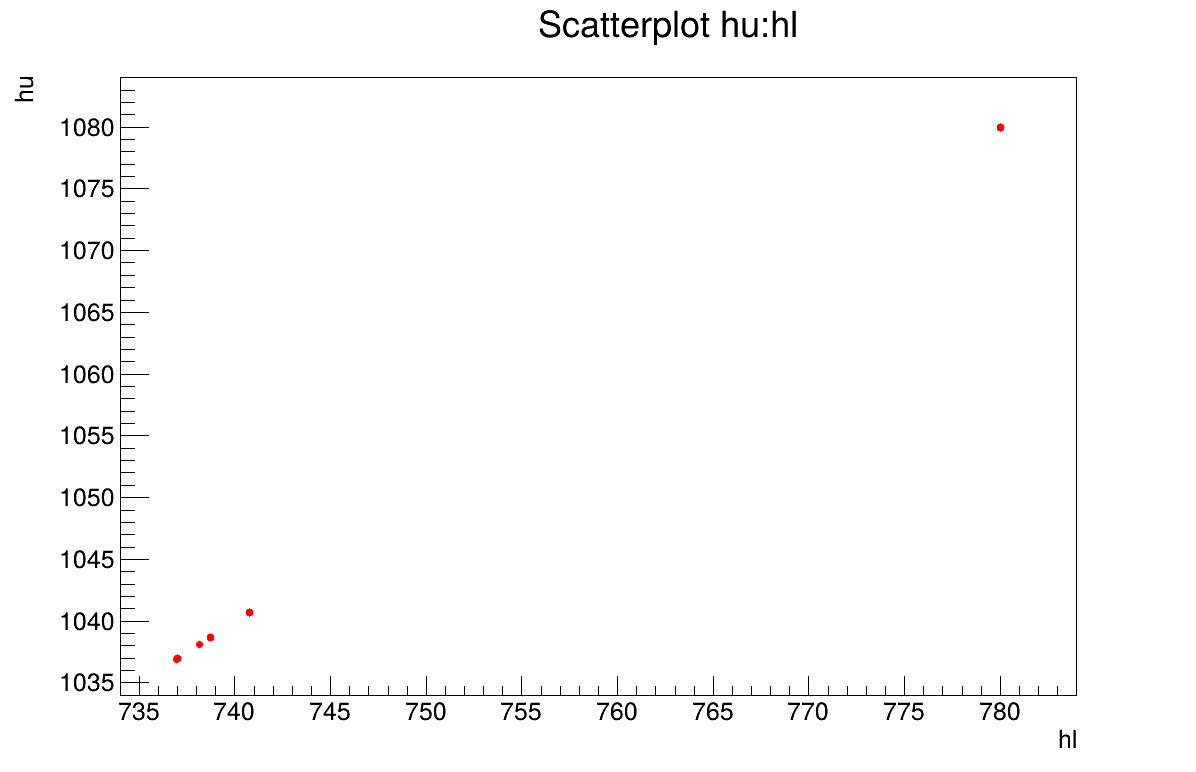
The final part is how to represents part of the results. There are many interesting point in this discussion: the residual, which are estimated using the mean of both parameters, are shown in Figure XIV.109. The fact that it is normally-distributed residual for the a posteriori estimations shows that the model is correct even though looking at the second plots, the parameters distribution, shows that there is large variety of solutions possible, see Figure XIV.110. This is a problem of identifiability as there are an infinity of solutions that could give the same results, and this can be seen by looking at the correlation matrix shown in Section XIV.12.6.3.
Processing calibrationMinimisationFlowrate2DVizir.py...
--- Uranie v4.10/0 --- Developed with ROOT (6.32.08)
Copyright (C) 2013-2025 CEA/DES
Contact: support-uranie@cea.fr
Date: Fri Feb 21, 2025
first 100
Genetic 1
Generation : 1, rang max 23
Nb d'evaluation : 100, taille de la Z.P. : 0
Generation : 2, rang max 23
Nb d'evaluation : 465, taille de la Z.P. : 1
Generation : 3, rang max 8
Nb d'evaluation : 963, taille de la Z.P. : 6
Generation : 4, rang max 0
Nb d'evaluation : 1617, taille de la Z.P. : 24
Genetic converge 1617
************************************************************************************
* Row * tdsPar__n * hu.hu * hl.hl * agreement * rgpareto. * generatio *
************************************************************************************
* 0 * 0 * 1038.1302 * 738.13383 * 0.3639076 * 0 * 3 *
* 1 * 1 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 2 * 2 * 1040.7058 * 740.77116 * 0.3639018 * 0 * 3 *
* 3 * 3 * 1079.9545 * 780 * 0.3639024 * 0 * 3 *
* 4 * 4 * 1040.7058 * 740.77116 * 0.3639018 * 0 * 1 *
* 5 * 5 * 1038.6638 * 738.70819 * 0.3639025 * 0 * 3 *
* 6 * 6 * 1040.7058 * 740.77116 * 0.3639018 * 0 * 3 *
* 7 * 7 * 1036.9776 * 736.98122 * 0.3639076 * 0 * 3 *
* 8 * 8 * 1036.9776 * 736.98122 * 0.3639076 * 0 * 3 *
* 9 * 9 * 1038.6638 * 738.70819 * 0.3639025 * 0 * 3 *
* 10 * 10 * 1036.9776 * 736.98122 * 0.3639076 * 0 * 2 *
* 11 * 11 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 12 * 12 * 1036.9776 * 736.98122 * 0.3639076 * 0 * 3 *
* 13 * 13 * 1040.7058 * 740.77116 * 0.3639018 * 0 * 2 *
* 14 * 14 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 15 * 15 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 16 * 16 * 1038.6638 * 738.70819 * 0.3639025 * 0 * 3 *
* 17 * 17 * 1040.7058 * 740.77116 * 0.3639018 * 0 * 3 *
* 18 * 18 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 19 * 19 * 1036.9776 * 736.98122 * 0.3639076 * 0 * 3 *
* 20 * 20 * 1036.9042 * 736.96108 * 0.3639019 * 0 * 3 *
* 21 * 21 * 1038.6638 * 738.70819 * 0.3639025 * 0 * 3 *
* 22 * 22 * 1080 * 780 * 0.3639083 * 0 * 3 *
* 23 * 23 * 1080 * 780 * 0.3639083 * 0 * 3 *
************************************************************************************
2x2 matrix is as follows
| 0 | 1 |
-------------------------------
0 | 1 1
1 | 1 1
hl is 752.4454 +- 19.946252
hu is 1052.4192 +- 19.959796