Documentation
/ Guide méthodologique
: 
| VIII.3. The Circe method | ||
|---|---|---|
 | Chapter VIII. The Uncertainty modeler module |  |
The Circe method is a statistical approach which is applied as an alternative to the expert judgement, used to determine the uncertainty of physical model's parameters. These uncertainties can be tricky to estimate as some of these parameters might not be directly measurable. However, it might be possible to use SET (separate-effect tests) experiments, which are sensitive to the physical model, to derive an estimation of these uncertainties.
As already stated previously, CIRCE (which stands for "Calcul des Incertitudes Relatives aux Correlations
Elementaires") is a statistical method in which the uncertainties are defined through random variables, mean values
and standard deviations [Circe,DeCrecy01]. Usually, if one considers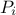 
the non-observed parameters (
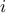being the number of these parameters, limited here to a certain number
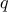), one can write the following
equation
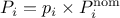
The physical parameter is then expressed as a function
of a nominal value (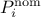
) and a multiplier coefficient 
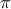. A relation can be constructed between these multipliers and the parameters considered by CIRCE, as
The nominal value of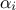 
is set to 0 (leading to a nominal value of the influential physical model equal
to 1). The other inputs needed by the method are the observed data (or responses) that will be hereafter called
(
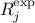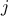being a realisation of the SET experiment), and
the corresponding code result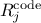 
. CIRCE combines the difference between the experimental and the code results (
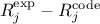) with the
derivatives of each code response with respect to each parameter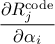 
. It is
also possible to take into account the experimental uncertainties of the response, called hereafter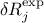 
. This procedure should
lead to the estimation, for every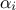 
parameter, of its mean value 
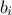(for bias) and its standard deviation, 
.
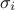In order to perform this estimation, there are two main hypothesis done by the CIRCE method:
the linearity between the code response and each parameter
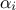. This hypothesis is clearly visible since first-order derivatives
are used for the estimation (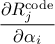). It is further discussed in Section VIII.3.1.1.
the normality of the
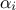parameters. An hypothesis on the PDF of CIRCE parameters is indeed compulsory, leading to the
hypothesis of normality or lognormality of the 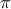multiplier if respectively the additive or exponential change of variable is
used in Equation VIII.1. This is further discussed in Section VIII.3.1.2.
For every response, the quantity of interest is 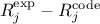which can as well be written as, if one notes
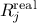the real
value of the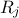 
response,
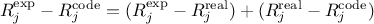. It is the sum of
two independent random variables:
(
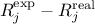): the experimental uncertainty which obeys a centered normal law of known standard
deviation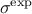 
.
(
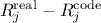): which is obtain from a first order development as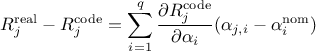 
In this definition,
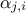is the unknown value to be given to the i-Th parameter so that
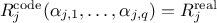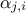( being different for every response) and
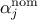is the nominal value of this i-Th parameter (generally 0).
If one gathers all the information about the system described up to now, the problem can be summarised as
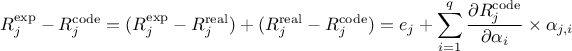
In this expression, on can discuss the different contributions:
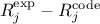- and 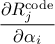are known.
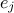is a realisation of
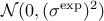where 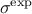is also known.
The
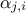are
unknown. The only available information can be extracted through their statistical features: their bias
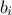and their standard
deviation .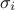
There will be several solutions possible for the vector of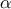 
, leading to a needed choice among them. The criterion chosen to do so is the
maximum of likelihood, which obliges to make an hypothesis on the form of the law followed by the 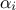parameters. The normal hypothesis is
then chosen.
| |  | |
| VIII.2. Tests based on the Empirical Distribution Function ("EDF tests") |  | References |