Documentation
/ Manuel utilisateur en Python
: 
| IX.4. Global solver | ||
|---|---|---|
 | Chapter IX. The Reoptimizer module |  |
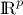spaces have no
ordering relations when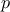 
is greater
than 1. As a consequence, finding the minimum of a function the output of which is defined in such a space has no
meaning. Multicriteria optimisation solves this problem by finding the inputs corresponding to the Pareto
frontier in the costs space.
The evolutionary algorithm library Vizir, allows to perform multicriteria optimisation with a global approach, and is available in Uranie. It is first introduced in a broad picture (even though more details can be found in [metho]) before considering the different solvers available and their possible configuration. We have also illustrate its use in a simple example that can be found in Section XIV.10.3.
Figure IX.2. Schematic description of the requested steps of an optimisation procedure once this one is performed with Vizir
 |
The global organisation of an analysis performed within Uranie with the Vizir package is as followed: the user
request a certain number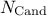 
of elements to describe correctly the Pareto set and front.
The first step is to create randomly, only using the research space definition, a population of the requested size. An evaluation is performed for all candidates, meaning that the criteria and constrains will be tested and the results will be stored in a vector for all candidates. All the calculation concerning a candidate will count as one evaluation (this notion will be important later on when considering the number of evaluation
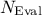). This step (the turquoise blue box in Figure IX.2) is followed by
the ranking of all the candidates (red step in Figure IX.2).
As already discussed, ranking single criterion results is simple because there is an obvious relation order, but this is not the case when dealing with multi-criteria. The chosen solution in the Uranie implementation is to affect a rank to a candidate under study, corresponding to the number of other candidates that dominate it. The best candidates have then a rank 0 (they are not-dominated), following by rank 1, rank 2... With the ranking step completed the next step is to test whether the algorithm has converged or not.
The test of convergence can reach three possible states:
all the tested candidates are not-dominated. This means the algorithm have converged and the loop will stop as the objective of having a description of both Pareto set and front is achieved.
not all candidates are not-dominated but the maximum number of evaluation has been reached. In this case, the algorithm stopped as well but this time without having converged. Restart the algorithm with different configuration might be a possibility.
not all candidates are not-dominated and the maximum number of evaluation is not reached.
In the latter case, a certain fraction of the candidates will be selected and used as a new starting point to recreate a new population. A fraction
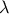is indeed kept (this fraction value being set by changing the survival rate
in the genetic case, whose default value is 40%) in order to produce a new generation that will hopefully
converge better than the current one. The evolutionary algorithm uses the selected fraction (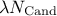
) to complete the total population (meaning re-generating 
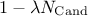). This procedure is explained more deeply, in the case of a genetic algorithm, in [metho].
The TVizir2 and TVizirIsland classes are the
TMaster subclass for global optimizer, the former being the more commonly used disregarding
the chosen solver and runner. The latter is dedicated to the island principle: instead of
growing a large population,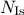 
populations are defined (this parameter can be changed by the dedicated
setIsland(int) method) and are growing independently, exchanging inhabitants from time to
time.
The setSize may be used to configure this. The first argument defines the population size
(default to 250). The second optional argument defines the maximum number of evaluations that the solver may use
(default to 100 000). The third optional argument defines the number of items born to create a new generation
(default to 50).
The Vizir solvers, that are interfaced with Uranie, are:
TVizirGenetic, a genetic algorithm using a diploid representation.TVizirSwarm, a particle swarm algorithm.TVizirSimplex, a Nelder Mead Simplex variant, adapted to work with a population, and to deal with multiobjective problem.
The TVizirGenetic (whose principle and vocabulary is define in [metho]) can be
configured using the following methods:
setMutationRate, defines the rate of population items that are muted during creation. Default value is 0.01 (1%).setHomozygoteRate, defines the rate of population considered as homozygote. Default value is 0.5 (50%).setSurvivalRate, obsolete, defines the rate of population items that survive at each generation. use setSize instead. Default value is 0.4 (40%).
The TVizirSwarm behaviour can be configured using the following methods:
setLocalSize, defines the particle memory size: its size and a generation step size.
The particle number is defines using the third parameter of
setSize method (generation item number).
It is half of it. No specific method is actually provided.
The global solvers discussed here have dedicated methods to call many-objective algorithms. An example of implementation can be shown in Section XIV.10.4.
setMogaDiversity(int val=0)setCrowdDiversity(int vois=0)setPairDiversity(int vois=0)setIbeaDiversity(double k=0)setKneeDiversity(int vois=0, double taux=0.0);setMoeadDiversity(int cut1, int cut2=0, int vois=0)setStoppingCriteria(int stop=0)
| |  | |
| IX.3. Local solver |  | Chapter X. The Metamodel Optimization module |