Documentation
/ Guide méthodologique
: 
| V.7. The Johnson relative weight | ||
|---|---|---|
 | Chapter V. Sensitivity analysis |  |
This section introduces indices whose purpose is mainly to obtain good estimators of the Shapley's values defined in Section V.1.1.4. The underlying assumption is to state that the model can be considered linear so that the results can be considered as proper estimation of the Shapley indices (with or without correlation between the input variables).
The idea here is very similar to the standard regression coefficients introduced in Section V.1.1.1, as one will use orthogonal transformation to represent our data, with dependent inputs. The method has been introduced by Johnson in [johnson2000heuristic] and its principle can be split into three steps:
transform the dependent input variables
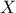through a linear transformation into 
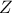so that 
;
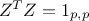compute sensitivity index of
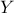with respect to ;
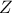reconstruct the sensitivity index of
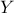with respect to the component of .
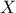Practically, the method proposed by [johnson2000heuristic] relies on the singular value
decomposition of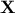 
,
written as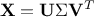 
for which 
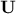, contains the eigenvectors of 
, 
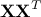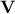contains the eigenvectors of 
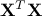and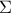 
is a diagonal matrix containing the singular values of
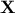. From there, the
best-fitting orthogonal approximation of 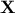can be obtained (c.f.
[johnson1966minimal] for the demonstration) as
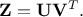
The second steps consists in regressing 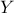onto 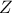, which is obtained by
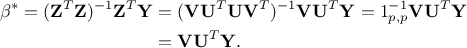
The squared elements of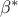 
represent the proportion of predictable variance in 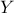accounted for by the 
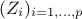, but in the case where two or more original variables
are highly correlated, the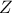
variables are not a close representation of the 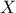ones. To take this into account, Johnson proposed to regress 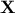onto 
, leading to other weights defined as:
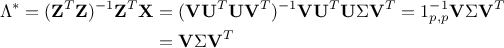
From there, the variance of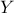
explained by 
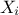can be written
as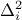 
and
estimated from the following formula
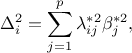
where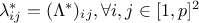 
and bearing in mind that
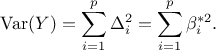
The resulting sensitivity indices are written
| |  | |
| V.6. Fourier-based methods |  | V.8. Sensitivity Indices based on HSIC |