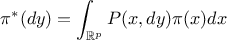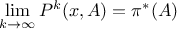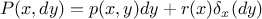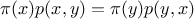Documentation
/ Guide méthodologique
: 
| VII.5. The Markov-chain approach | ||
|---|---|---|
 | Chapter VII. The Calibration module |  |
Unlike the Monte-Carlo methods already discussed in Chapter III to obtain design-of-experiments and which usually provides independent samples (which means that the successive observations are statistically independent unless correlation is purposely injected), the Monte-Carlo techniques describe here are called "Markov-chain" and they provide dependent samples as the estimation of the i-Th iteration only depends of the value of the previous one, the (i-1)Th.
An usual approach to explain the Markov-chain theory on a continuous space is to start with a transition kernel
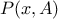where
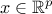and
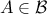, where
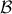is the Borel
-algebra on
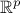[wakefield2013bayesian]. This transition kernel is a conditional distribution function that
represents the probability of moving from 
to a point in the set 
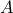. It is interesting to notice two properties: 
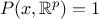and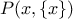 
is not necessarily zero, meaning than a transition
might be possible from to
. For a single estimation, from a
given starting point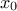 
, this
can be summarised as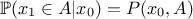 
.
The Markov-chain is defined as a sequence using this
transition kernel a certain number of time, leading to the k-Th estimation (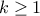
) 
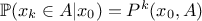where
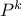denotes the k-Th
iteration of the kernel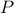 
[tierney1994markov].
The important property of a Markov-chain is the invariant distribution,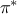 
, which is the only distribution satisfying the following
relation
where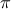 
is the density with respect to the Lebesgue measure of
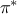(meaning
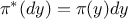). This invariant distribution is an equilibrium distribution for the chain that is the target of
the sequence of transition, as
The Monte-Carlo Markov-chain approach (hereafter called MCMC) is the following one: the invariant distribution is
considered known, as it is the one from which one wishes to sample, while the transition kernel is unknown and to be
determined. This might seem to be "the proverbial needle in a haystack" but the idea is to be able to write the
target kernel through a transition kernel probability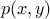 
(describing the move from to 
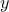) as
where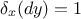 
and 0 otherwise, while
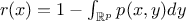is the probability that the chain remains at its current location. If the transition part of this
function,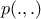 
,
satisfies the reversibility condition (also called time reversibility,
detailed balance, microscopic reversibility...)
then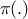 
is the invariant density of 
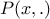[tierney1994markov].
In the Metropolis-Hasting approach, the candidate-generating density is traditionally denoted
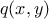. If this density
satisfies the reversibility condition in equation Equation VII.13 for
all and the search is over (but this is very unlikely). What's
more probable is to find something like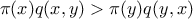 
that states that moving from to 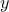is happening too often (or the other way too scarcely).
The proposed way to correct this is to introduce a probability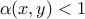 
where this 
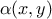is called the probability of
move that is injected in the reversibility condition to help fulfil it. Without
getting in too much details (see [chib1995understanding] which nicely discusses this), the
probability of move is usually set to
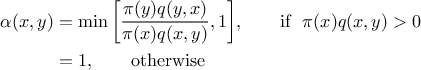
If the chain is currently at a point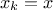 
, then it generates a value 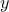accepted as 
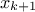with the probability 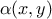. If rejected the chain remains at the current location and another
drawing is performed from there.
With this, one can define the off-diagonal density of the Metropolis-Hasting kernel as function,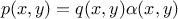 
if
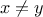and 0 otherwise and
with thanks to equation Equation VII.12, one has the invariant distribution for
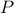[tierney1994markov].
Warning
Two important things to notice herethe obtained sample is obviously not independent as the k+1-Th location is taken out from the k-Th one.
the very first drawn locations are usually rejected as part of the burn-in (also called warm-up) process. As discussed above, the algorithm needs a certain number of iteration to converge through the invariant distribution.
The idea here is to choose a family of candidate-generating densities that follows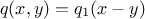 
where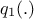 
is a multivariate density
[muller1991generic], a classical choice being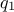 
set as a multivariate normal density. The candidate is indeed drawn as
current value plus a noise, which is the origin of the random walk name.
Once the newly selected configuration-candidate is chosen, let's call it ,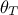 
the comparison with respect to the latest
configuration kept, called here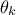 
, is done through the ratio of likelihood, which allows to get rid of any constant factors and
should look like this once transformed to its log form:
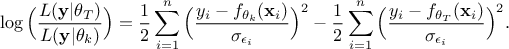
This result is then compared to the logarithm of a random uniform drawing between 0 and 1 to decide whether one should keep this configuration (as usually done in Mpnte-Carlo approach, see [chib1995understanding]).
There are few more properties for this kind of algorithm such as the acceptation rate, that might be tuned or used as validity check according to the dimension of our parameter space for instance [gelman1996efficient,roberts1997weak] or the lag definition, sometimes used to thin the resulting sample (whose usage is not always recommended as discussed in [link2012thinning]). These subjects being very close to the implementation choices, they are not discussed here.
| |  | |
| VII.4. The Approximation Bayesian Computation techniques (ABC) |  | Chapter VIII. The Uncertainty modeler module |